Cтуденттерге өзіндік есептер

1. Тәуелсіз n сынақта оқиға тұрақты ықтималдықпен пайда болады.

62.1.n=1500 болғанда салыстырмалы жиіліктің p=0,4 ықтималдықтан ауытқуының абсолют шамасы 0,02 – ден кем болатындығыныңықтималдығын табу керек.

2. 2.n=1500 және p=0,4 болғанда оқиғаның пайда болуының саны мына аралықтарда жататындығының ықтималдығын табу керек.

а) 570 – тен 630 – ға дейін

б) 600 – ден 660 – қа дейін

с) 620 – дан 680 – ге дейін

г) 580 – нен 640 – қа дейін

3. 3.n=1200, p=2/3 болғанда салыстырмалы жиіліктің ықтималдықтан (p=2/3) ауытқуының абсолют шамасының ықтималдығы 0,985 – ке тең болуы үшін салыстырмалы жиілік қандай аралықта жатуы керек?

4.Салыстырмалы жиіліктің ықтималдықтан (p=3/8) ауытқуының абсолют шамасының 0,01 – ден кем болуының ықтималдығы 0,995 – ке тең болуы үшін қанша тәуелсіз сынақтар жасау керек?

5. Автоматты станокта стандартты деталь дайындау ықтималдығы 0,9 – ға тең. Алынған 5 детальдің үшеуі стандартты болуының ықтималдығын табу керек.

6. Әрбір 16 тәуелсіз сынақта оқиға тұрақты 0,7 ықтималдықпен пайда болады.Ең ықтимал санды табу керек.

7. Әрбір атыста нысанаға тигізу ықтималдығы 0,7 – ге тең. 300 атыста нысанаға 240 рет тигізудің ықтималдығы қандай?

8. Сапасыз деталь жасаудың ықтималдығы 0,02 – ге тең. 400 деталь жасап шығарғанда оның ішінде 7 – ден 10 – ға дейін сапасыз деталь болуының ықтималдығын табу керек.

9. Телефон станциясында әрбір тапсырыс қабылдағанда қате жіберу ықтималдығы 0,009 – ға тең. Станция 1000 заказ қабылдады. Сонда 9 заказды қате қабылдауының ықтималдығы қандай?

10. Зауыт дайындайтын бұйымдардың 60% - ті бірінші сортпен шығарылады. Қабылдаушы кез келген 200 бұйымды қабылдап алды. Осы 200 бұйымның ішінде 120 – дан 150 – ге дейін бірінші сортты бұйымдар болатындығының ықтималдығы қандай?

11. Урнаға бірдей бір қара, бір қызыл және бір ақ шарлар салынған. Урнадан бір шар алынып, сосын қайта урнаға салынып, тәжірибе бес рет қайталанды. Сонда қара шарлар мен ақ шарлар кем дегенде екі рет алынғандығының ықтималдығын тап.

12. Нысанаға ішкі бір дөңгелек және екі концентрлік сақинадан тұрады.Осы нысанаға 10 ақ атылды. Әрбір атыста аталған облыстарға тию ықтималдықтары сәйкес 1/15, 1/2 және 1/7 тең.10 атыста ішкі дөңгелекке үш оқ, бірінші сақинаға 6 оқ және екінші сақинаға 1 оқ тиетіндігінің ықтималдығын тап.

13. Лотереяда бір билетке ұтыс шығуының ықтималдығы 0,3 – ке тең болғанда, алынған 10 билеттің ішінде ұтыс шығуының ең ықтимал саны қандай?

14. Тәуелсіз сынақтарда оқиғаның пайда болу ықтималдығы 0,5 – ке тең.196 сынақта оқиғаның 100 рет пайда болуының ықтималдығы қандай?

15. Теңгені 5 рет лақтырғанда гербтің кем дегенде 2 рет пайда болуының ықтималдығы қандай?

16. Белгілі бір оқиғаның 300 тәуелсіз сынақтарда пайда болу ықтималдығы 0,6 – ға тең. Оқиғаның пайда болуы 250 реттен аспайтындығының ықтималдығын табу керек.

17. Егер әрбір ағаштың өсіп шығуының ықтималдығы 0,8 – ге тең екендігі белгілі болса, онда отырғызылған 400 ағаштан 104 ағаштың өсіп шықпайтындығының ықтималдығы қандай болады?

18. Урнада 100 ақ 80 қара шарлар бар. Урнадан кез-келген шар алынып түсін анықталғасын қайтарылады.Ақ шар шығуының ең ықтимал саны 11 – ге тең болу үшін қанша сынақ жүргізу керек?

19. Фабрика жасап шығарған бұйымдардың 25%- ті сапасыз болатындығы белгілі еді. Тексеруге кез- келген 8 бұйым алынды. Осы сегіз бұйымның алтауының сапасыз болуының ықтималдығы қандай?

20. Белгілі бір оқиға 25 тәуелсіз сынақта 0,7 ықтималдықпен пайда болады. Оқиғаның пайда болуының ықтимал санын табу керек.

21. Гаражда 5 машина бар. Кез-келген бір моментте машиналардың жұмыс істеу ықтималдығы 0,8 – ге тең.Қалаған бір моментте үш машинаның жұмыс істеуінің ықтималдығы қандай?

22. Егер алынған кез-келген детальдің жарамсыз болуының ықтималдығы 0,1 – ге тең екендігі белгілі болса, онда жарамды детальдардың пайда болуының ең ықтимал саны 50 – ге тең болуы үшін қанша деталь алу керек?

23. Оқиғаның 144 тәуелсіз сынақтарда пайда болу ықтималдығы 0,8 – ге тең. Осы сынақтарда оқиғаның 120 рет пайда болуының ықтималдығы қандай?

24. Семьядағы 7 баланың төртеуі ұл және үшеуі қыз екендігінің ықтималдығы қандай?

25. Цехтағы 6 мотордың әрқайсысының белгілі бір моментте істеп тұрғандығының ықтималдығы 0,8 – ге тең. Белгілі бір моментте 4 мотордың істеп тұруының ықтималдығын табу керек.

Кездейсоқ оқиғалар.

х …

p p p p … p

Мысал 1. Жәшікте барлығы 10 шар бар, олардың 7-і қара 3-і көк шарлар. Жәшіктен кез-келген 5 шар алынды. Сол 5 шардың үшеуі қара болуының ықтималдығы қандай?

Шешуі: Осындай мазмұнды есепті классикалық анықтаманы және комбинаторикадағы қосу және көбейту ережелерін пайдаланып шығаруға болады. Бұл есепті солай шығарса болады.

Енді осы есепті жалпы түрде келтірейік.

Мысал 2. Жәшікте барлығы N шарлар бар, оның ішінде n қара шар бар, ал (N-n) – көк шарлар. Жәшіктен кез-келген m шар алынды.Сол алынған m шардың ішінде к қара шар болуының ықтималдығы қандай?

Шешуі: х-жәшіктен алынған шарлар саны. Бұл кездейсоқ шаманың мүмкін мәндері 0,1,2,…, m.

Жәшіктегі N шардан m шарды әртүрлі С жолмен алуға болады, ал n қара шарлардан к шарды әртүрлі С жолмен алуға болады, сонда алынған m шардың ішінде m-к көк шарлар болғандықтан барлық N-n көк шарлардан m-к көк шарды С жолмен алуға болады. Сонымен жәшіктен алынған шардың к қара шарын С жолмен, ал қалған m-к көк шарды С жолмен алуға болады екен. Олай болса комбинаторикадағы көбейту ережесін қолдансақ, алынған m шардың іщінде к- қара шар, m-к көк шар болуы С жолмен анықталады. Сонда ықтималдықтың классикалық анықтамасы бойынша

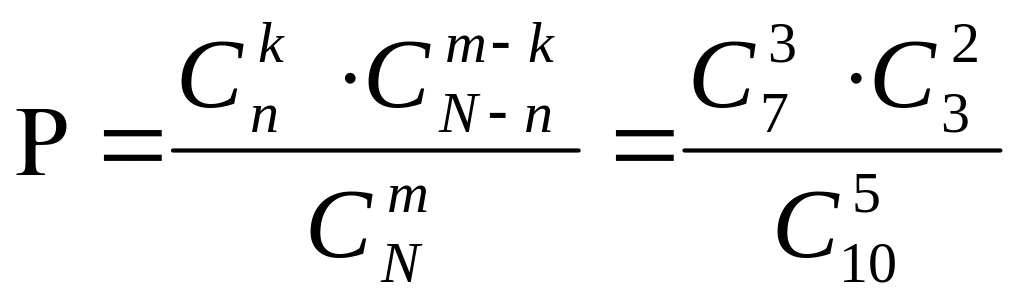
болады.

Сөйтіп Х-кездейсоқ шама гипергеометриялық үлестіріммен берілгеніне көз жеткіздік.

Мысал 3. Дискретті кездейсоқ шама мына үлестіріммен берілсін

Х -1 0 1 2

P 0,2 0,4 0,2 0,2

Сандық сипаттамаларын тап.

Шешуі:

М(Х)=-1

Мысал 4

Теңге үш рет лақтырылсын. Кездейсоқ шама Х ретінде елтаңбаның пайда болу санын қарастырамыз.

1. Үлестірім қатарын жазу керек.

2. Үлестірім көпбұрышын салу керек.

3. М(х), D(х), (х)-тарды табу керек.

Шешуі: Бұл кездейсоқ шама Х-тің мүмкін мәндері 0, 1, 2, 3.Себебі теңгені үш рет лақтырғанда елтаңба не пайда болмауы мүмкін, не бір рет пайда болуы мүмкін т.с.с. Ал әрбір лақтырғанда елтаңбаның пайда болу ықтималдығы 0,5 – ке тең.Олай дегеніміз теңге лақтырғанда негізінен не елтаңба, не цифр пайда болады, ал теңгенің симметриялығын ескерсек бұл екеуінің пайда болу ықтималдығы тең.Сондықтан бұл кездейсоқ шама Х-тi биномдық үлестірім заңымен сипаттауға болады. Үлестірім қатарын жазайық:

х 0 1 2 3

p C C C C

немесе

х 0 1 2 3

p 1/8 3/8 3/8 1/8

Бұл жерде

орындалады.

2. Үлестірім көпбұрышын салайық

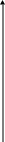
P 1

3 /8

1 /8

2 3 х

3. Математикалық үмітті есептейміз:

М(Х)=0

Ал дисперсияны әдетте жеңілдетілген формуламен есептейді. Ол үшін кездейсоқ шаманың үлестірім қатарын жазып алу керек.

х 0 1 4 9

p 1/8 3/8 3/8 1/8

Cонда

М(Х )=0

D(Х)=3- ,

Сондай-ақ бұл мысалдағы кездейсоқ шаманың биномдық үлестіріммен берілгенін ескерсек, онда сандық сипаттамаларды пайдаланып та есептеуге болады

М(Х)=3 D(Х)=3

Мысал 5. Берілген партияның 10 проценті сапасыз бұйымдар. Кез келген 4 бұйым алынды. Осы төрт бұйымдардың ішінде сапасыз бұйымдардың пайда болу санының үлестірім заңын жазу керек.Сандық сипаттамаларын есептеу керек.

Шешуі: х-сапасыз бұйымдардың пайда болуының саны. Әрбір сапасыз бұйымның пайда болу ықтималдығы 0,1 – ге тең, себебі берілген партияның 10 проценті сапасыз бұйымдар.Бұл кездейсоқ шама биномдық үлестірім заңымен берілген.Мұнда n=4, p=0,1 , q=0,9

Сонда

х 0 1 2 3

р С С С С С

немесе

х 0 1 2 3 4

p 0,6581 0,2916 0,0486 0,0036 0,0001

Е нді математикалық сипаттамаларын табайық

М(Х)=4 , D(Х)=4 , .

Мысал 6. Дискретті кездейсоқ шама үлестірім қатарымен берілген

Х 2 4 5 6 8

p 0,1 0,2 0,3 0,1 0,3

М(Х), D(Х) , тарды табу керек.

Шешуі:

Енді D(Х)-ті есептеу үшін мына шаманың үлестірім таблицасын құрамыз

4 16 25 36 64

p 0,1 0,2 0,3 0,1 0,3

Сонда D аламыз.

Мысал 7. Урнада 5 ақ және 50 ақ шарлар бар. Урнадан кез келген шар алынып түсі анықталғаннан кейін урнаға қайтарылады.Кездейсоқ шама Х-тәуелсіз 10 сынақта ақ шар пайда болуының саны. Осы кездейсоқ шаманың үлестірім заңын жазыңыз.

Шешуі: Бұл мысалда сынақ кезінде ақ шар пайда болу ықтималдығы p=5/55=1/11 сынақ саны n=10. Олай болса қарастырып отырған кездейсоқ шаманы биномдық заңмен берсек, онда үлкен арифметикалық есептеулерге кезігеміз.Сондықтан бұл кездейсоқ шаманы Пуассон үлестірім заңымен беруге болады. Сөйтіп, кездейсоқ шаманың мүмкін мәндері 0, 1, 2, …10.

Ал кездейсоқ шаманың мүмкін мәндерінің сәйкес ықтималдықтары

, к=0, 1, 2, …,10.

Жеке жағдайда к=3 болса, биномдық үлестірім бойынша

Пуассондық үлестірім бойынша

Мысал 8. Екі атқыш әрқайсысы өз нысанасына бір-бірден атыс жүргізді. Бірінші атқыш үшін нысанаға тигізудің ықтималдығы , ал екінші атқыш үшін - .Кездейсоқ шамалар -бірінші атқыштың нысанаға тигізу саны, -екінші атқыштың нысанаға тигізу саны, ал z= -екі кездейсоқ шамалардың айырымы.Оның математикалық сипаттамаларын: М(z), D(z)-тарды табамыз.

Шешуі: Әуелі кездейсоқ шамалардың үлестірім кестесін жазамыз:

х 0 1 х 0 1

p q p p q p

Осыдан

М(z)=М(х )-М(х )=p -p , D(х )=p q

D(х )=p q , D(z)=p q +p q

М ысал 9. Екі тәуелсіз кездейсоқ шамалар Х және У үлестірім кестелерімен берілген

х 0 3 4 у 2 3

p 0,2 0,6 0,2 p 0,3 0,7

х+у, х -кездейсоқ шамалардың иатематикалық үміттері мен дисперсияларын тап.

Шешуі: Кестелерден

М(х)=2,6 , М(у)=2,7 , D(х)=1,84 , D(х)=0,21 табамыз. Сосын х және у тәуелсіз кездейсоқ шамалар екендігін пайдаланып

М(х+у)=2,6+2,7=5,3 D(х+у)=1,84+0,21=2,05

М(х )=2,6

табамыз.

Мысал 10. “Спортлото”ойынын ойнағанда белгілі бір ұтысқа шығатын спорттың түрлерін дәл табудың ықтималдығын тап.

Шешуі: Мұндағы х-ұтысқа шыққан спорттың түрлерінің саны.Бұл кездейсоқ шама гипергеометриялық үлестірім заңымен берілген.Мұнда N=49, m=6, n=6, k=1,2,3,4,5,6. Ойынның шарты бойынша ұтыс үш спорттың түрін дәл тапқаннан бастап төленеді.Сондықтан біз k=3,4,5,6 жағдайларын қарастырып, сәйкес ықтималдықтарды табалық

k=3 , k=4,

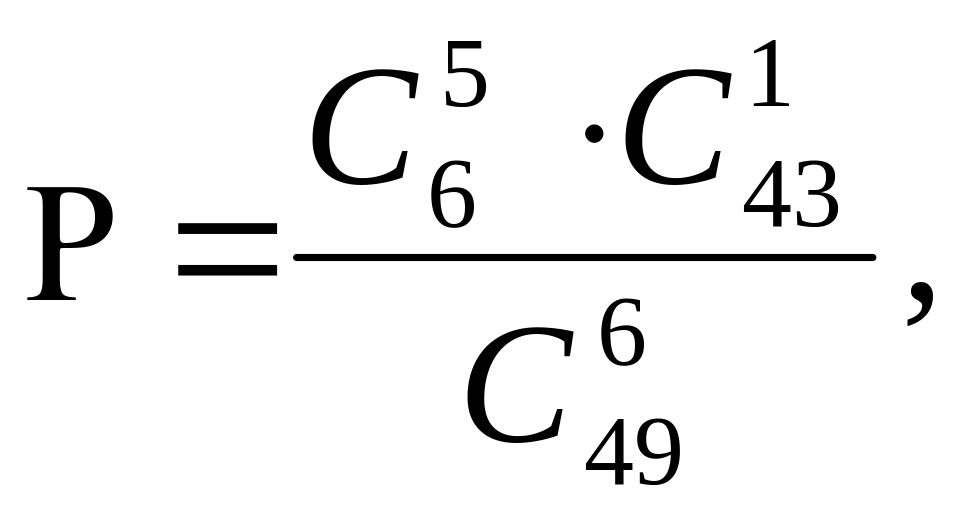k=5, k=6,

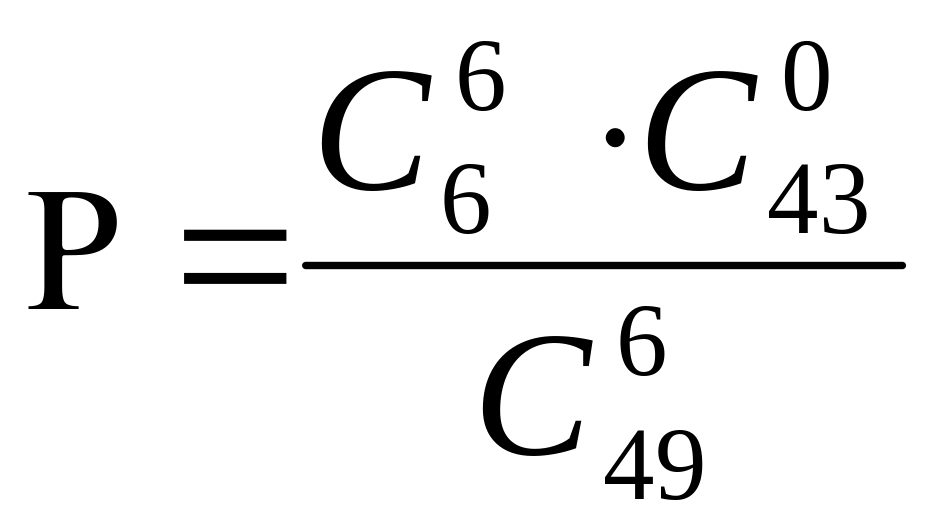
Сол сияқты к=5 және к=6 болғанда сәйкес ықтималдықтар

p және p=7,15

Мысал 11. Айталық 12 бұйымның 8-і бірінші сортқа жатады. Кезкелген 5 бұйым алынды. Сонда осы 5 бұйымның ішінде бірінші сортты бұйымдардың болуының үлестірім кестесін құрыңыз.

Шешуі: Есептің шарты бойынша N=12, m=5, n=8. Кездейсоқ шама Х.Оның мүмкін мәндері: 1,2,3,4,5. Мұнда мүмкін мәндер бірден басталуының себебі: 5 бұйымның ішінде кем дегенде бір бұйым бірінші сортқа жатады.

Сонда Р(х=k)=