Кесте 3
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
xi |
n |
ui |
niui |
niu2i |
niu3i |
niu4i |
ni(ui+1)4 |
305 |
3 |
-5 |
-15 |
75 |
-375 |
1875 |
768 |
315 |
5 |
-4 |
-20 |
80 |
-320 |
1280 |
405 |
325 |
10 |
-3 |
-30 |
90 |
-270 |
810 |
160 |
335 |
14 |
-2 |
-28 |
56 |
-112 |
224 |
14 |
345 |
19 |
-1 |
-19 |
19 |
-19 |
19 |
0 |
355 |
21 |
0 |
0 |
0 |
0 |
0 |
21 |
365 |
15 |
1 |
15 |
15 |
15 |
15 |
240 |
375 |
8 |
2 |
16 |
32 |
64 |
128 |
648 |
385 |
3 |
3 |
9 |
27 |
81 |
243 |
768 |
395 |
2 |
4 |
8 |
32 |
128 |
512 |
1250 |
|
|
|
|
|
|
|
|
Сегізінші тік жол есебіміздің дұрыстығына қажет.
Қажетті қосындының теңдігінен есептеуіміздің дұрыстығы дәлелденеді.
Шартты бірінші, екінші, үшінші, төртінші ретті моменттерді есептейміз.
Эмпирикалық үшінші және төртінші орталық моменттерді есептейміз
Һ=10,
Таңдаманың сандық сипаттамаларын есептейміз.
6) Таралым заңын алдын-ала таңдау үшін алдыменен ассиметрияменен эксцесстің есептелудегі қатесін табайық. Ол үшін
Кездейсоқ шаманың таралымының қалыпты болуы үшін ассиметрия мен эксцесс нөлге тең болуы керек. Біздің есебіміз бойынша ассиметрия мен эксцесс орташа квадрат қателіктерден мына теңсіздіктерді қанағаттандырады,
Бұл теңсіздіктер кездейсоқ шаманың Гаусс үлестіріммен таралуын көрсетеді.
Екіншіден полигон мен гистограмма графигі Гаусс қисығын көрсетеді.
Кездейсоқ шама Х, Гаусс таралылымен үлестірілсе, онда
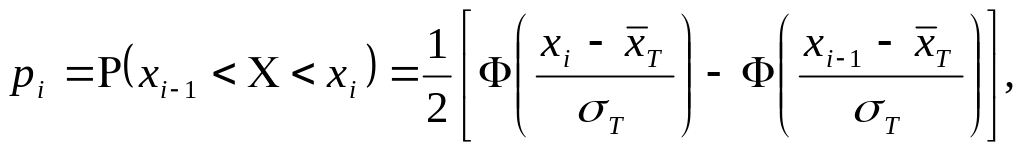
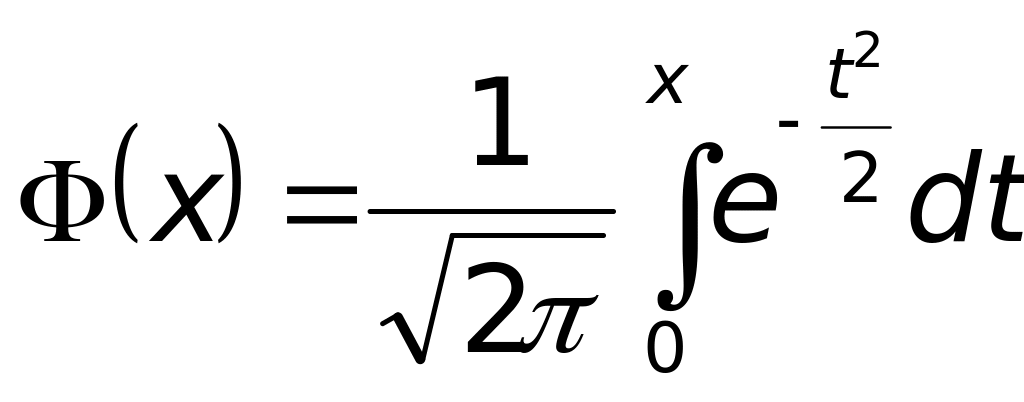-Лаплас
функциясы
Төртінші есептеу кестесін құрамыз:
i |
Интервал- дар
|
Эмпирикалық жиілік
|
|
|
|
|
|
Теоретика- лық жиіліктер
|
1 |
300-310 |
3 |
-2,4771 |
-1,9674 |
-0,4934 |
-0,4756 |
0,0178 |
2 |
2 |
310-320 |
5 |
-1,9674 |
-1,4577 |
-0,4756 |
-0,4279 |
0,0477 |
5 |
3 |
320-330 |
10 |
-1,4577 |
-0,9480 |
-0,4279 |
-0,3289 |
0,099 |
10 |
4 |
330-340 |
14 |
-0,9480 |
-0,4383 |
-0,3289 |
-0,1700 |
0,1589 |
16 |
5 |
340-350 |
19 |
-0,4383 |
-0,0714 |
-0,1700 |
0,0279 |
0,1979 |
20 |
6 |
350-360 |
21 |
0,0714 |
0,5810 |
0,0279 |
0,2190 |
0,1911 |
19 |
7 |
360-370 |
15 |
0,5810 |
1,0907 |
0,2190 |
0,3621 |
0,3621 |
14 |
8 |
370-380 |
8 |
1,0907 |
1,6004 |
0,3621 |
0,4452 |
0,0831 |
8 |
9 |
380-390 |
3 |
1,6004 |
2,1101 |
0,4452 |
0,4821 |
0,0369 |
4 |
10 |
390-400 |
2 |
2,1101 |
2,6198 |
0,4821 |
0,4956 |
0,0135 |
1 |
8) Пирсон критерийін пайдаланып эмпирикалық және теориялық жиіліктерді салыстырамыз
i |
|
|
|
|
|
|
|
1 |
3 |
2 |
1 |
1 |
0,5 |
9 |
4,5 |
2 |
5 |
5 |
0 |
0 |
0 |
25 |
5 |
3 |
10 |
10 |
0 |
0 |
0 |
100 |
10 |
4 |
14 |
16 |
-2 |
4 |
0,25 |
196 |
12,25 |
5 |
19 |
20 |
-1 |
1 |
0,05 |
361 |
18,05 |
6 |
21 |
19 |
2 |
4 |
0,21 |
441 |
23,21 |
7 |
15 |
14 |
1 |
1 |
0,07 |
225 |
16,07 |
8 |
8 |
8 |
0 |
0 |
0 |
64 |
8 |
9 |
3 |
4 |
-1 |
1 |
0,25 |
9 |
2,25 |
10 |
2 |
1 |
1 |
1 |
1 |
4 |
4 |
100 99 2,33 103,33
Бақылау:
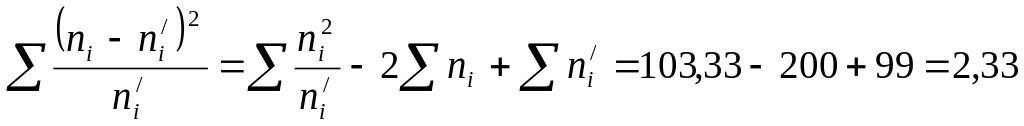
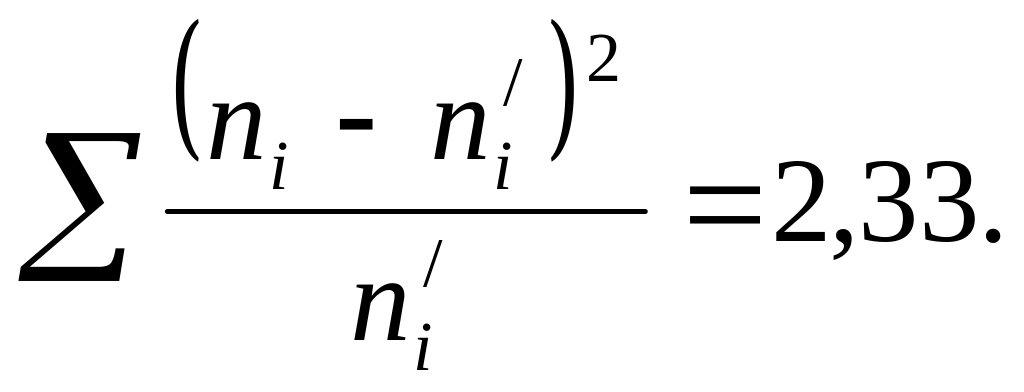
9) Математикалық үмітті мына формуланы пайдаланып
мұндағы
жоғарыда есептелген
t=1,96 Лаплас функциясының мәнінен табылады Ф(t)=0,95.
Қажетті есептеулерді орындағанда:
Сонда (344,75; 352; 42) – іздеп отырған сенімділік аралығы.