Есептер

1. Х және У кездейсоқ шамалардың систеиасының үлестірім заңы кесте арқылы берілген

У 0 1 2 3

Х

1 0,04 0,05 0,01 0,06

4 0,24 0,15 0,04 0,07

6 0,05 0,10 0,09 0,10

табу керек: 1. Х және У-тердің әрқайсысының үлестірім заңдарын;

2. болғандағы У-тің шарты үлестірім заңын;

3. Х пен У тәуелді ме?

4. Р(х<4,у<2)=?

5. Коррелиялық коэффициентті r .

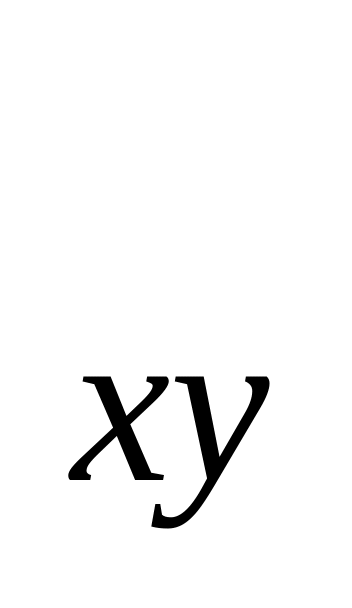3. Х және У кездейсоқ шамалар системасының үлестірім заңы кесте арқылы берілген.

Х -1 0 1

У

0 0 0,2 0,1

1 0,4 0,1 0,2

Табу керек: 1. Х және У – тердің әрқайсысының үлестірім заңдарын;

2.У=1 болғанда Х-тің шартты үлестірім заңдарын;

3. Х пен У тәуелді ме?

26. Екі атқыш бір нысанаға бір бірінен тәуелсіз екі атыс жасады. Біріншісінің нысанаға тигізу ықтималдығы 0,8, екіншісінікі – 0,6. Айталық Х-бірінші атқыштың нысанаға тигізген оқтарының саны, У – екінші атқыштың тигізген оқтарының саны. Табу керек: 1. Х және У кездейсоқ шамаларының системасының үлестірім заңын; 2. Х және У – тердің әрқайсысының үлестірім заңдарын.

27. Жәшікке бірдей 5 қызыл 2 жасыл және 3 көк шарлар салынған. Жәшіктен 3 шар алынды. Айталық Х-алынған қызыл шарлар саны, У-алынған жасыл шарлар саны болсын. Табу керек: 1.Х пен У – тердің үлестірім заңдарын; 2.(Х,У) систеиасының үлестірім заңы; 3. r - тап.

28. Х және У тәуелсіз кездейсоқ шамалар сәйкес [4;6] және [0;3] аралықтарында бірқалыпты үлестіріммен берілген.

Табу керек: 1. -терді; 2. F -терді; 3. (Х,У) системасының үлестірім тығыздығын; 4. F -ті; 5. Р(5<x<6,1<у<2)-ті.

26. (Х,У) системасы үлестірім функциясы арқылы берілген

Табу керек: 1. - үлестірім тығыздығын;

2. F Және F -функцияларын.

3. .

173. (Х,У) системасы үлестірім функциясының тығыздығы арқылы берілген

Табу керек: 1) а-тұрақты санын, 2)F(х,у) – үлестірім функциясын; 3) Р(0<x< 0<у<1)

174. (Х,У) системасы үлестірім функциясының тығыздығы арқылы берілген:

х,у-тің басқа мәндері үшін.

Табу керек: 1) а – тұрақты санын;

2) F(х,у) – үлестірім функциясын;

Кездейсоқ шамалар функциясы

Кездейсоқ оқиғалар системасын қарастыралық. Олардың әрқайсысының үлестірім заңдары белгілі болсын. Сонда кездейсоқ шамалар функциясы мына түрде беріледі

(2.4.1.)

Осы кездейсоқ шама у- тің үлестірім заңын табу керек.Біз бір кездейсоқ шаманың функциясын қарастыралық

(2.4.2)

Мұнда Х дискретті немесе үзіліссіз кездейсоқ шама болуы мүмкін.

1. Х-дискретті кездейсоқ шама үлестірім кестесімен берілген.

Сонда у – кездейсоқ шаманың үлестірім заңы.

у …

Р …

2. Х – үзіліссіз кездейсоқ шама f(х) үлестірім тығыздығымен берілген, сонда у – кездейсоқ шаманың үлестірім заңын жазу үшін оның үлестірім тығыздығын табу керек. Екі жағдай болуы мүмкін:

1.у= функциясы [a,b] аралығында монотонды-өспелі үзіліссіз және дифференциялданатын функция. Онда осы аралықта оның бір ғана (у) кері функциясы бар болады да g(у)=f(ф(у) орындалады. (2.4.3)

2. у= функциясы монотонды емес.

Сондықтан оның кері функциялары болады да

g(у)=

орындалады.

Мысал 1

Кездейсоқ шама үлестірімм таблицасымен берілген

х 0 1 2 3

Р 0,1 0,2 0,3 0,4

У=(4-х) cos функциясының үлестірім кестесін табыңыз.

Шешуі: Әуелі у- тің мүмкін мәндерін анықталық:

у=(4-0)cos у

у у

Сонымен

х -3 -1 2 4

Р

кестесін алдық.

Енді -лерді табалық.

Сөйтіп, ақырында

у -3 -1 2 4

q 0,2 0,4 0,3 0,1

үлестірім кестесін алдық.

Мысал 2. Кездейсоқ шама үлестірім тығыздығын берілген

у=х кездейсоқ шаманың үлестірім тығыздығын тап.

Шешуі: функциясы монотонды өспелі, үзіліссіз және дифференциялданатын функция. Сондықтан оның кері функция болады. Осыдан (2.4.3) формуланы пайдаланып

g(у)=

Мысал 3

Екі мерген бір-бірімен тәкелсіз нысанаға сәйкес 2 және 3 атыс жасайды. Біріншісінің нысанаға тигізу ықтималдығы 0,9, ал екіншісінікі – 0,8. Х,У – бірінші және екінші мергеннің нысанаға тигізулерінің сандары. Z=X+Ү, Z=XУ кездейсоқ шамалардың үлестірім кестесін жазыңыз. М(Х+У), М(ХУ)-терді табыңыз.

Шешуі: Х және У кездейсоқ шамалар биномдық үлестірім заңымен берілген. Сондықтан Бернулли формуласын пайдаланып

Х 0 1 2 У 0 1 2 3

Р 0,01 0,18 0,81 Ру 0,08 0,096 0,384 0,512

үлестірім кестелерін аламыз.

Енді Z=X+Ү, Z=XҮ кездейсоқ шамаларының мүмкін мәндерін х және х табалық. Олардың ықтималдықтары арқылы есептеледі. Енді және мүмкін мәндерін есептелік.

Р

Осыдан

х+у 0 1 2 3 4 5

Р 0,0008 0,0024 0,0276 0,152 0,4032 0,41472

ху 0 1 2 3 4 6

Р 0,01792 0,01728 0,14688 0,09216 0,31104 0,41472

үлестірім заңдарын аламыз.

Сондай-ақ М(х+у)=4,2 М(ху)=4,32006

Математикалық статистикада тәуелсіз қалыпты үлестіріммен берілген кездейсоқ шамалардың функциясы болып келетін үлестірім заңдарымен берілген кездейсоқ шамалар қарастырылады. Солардың жиі кездесетін үшеуін төменде қарастырамыз.

1. Хu – квадрат үлестірім ( 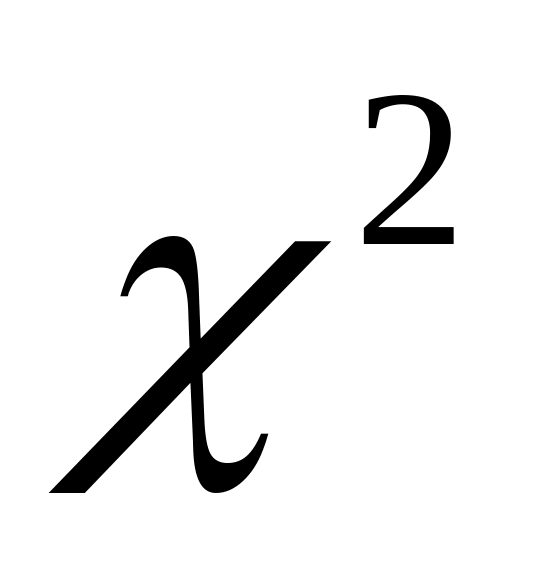-үлестірім).

Айталық Х -тәуелсіз қалыпты кездейсоқ шамалар берілсін және а=0, =1 болсын.

Енді

к ездейсоқ шаманы қарастыралық.

Бұл кездейсоқ шаманың үлестірім заңы - үлестірім деп аталады. Мұнда v – еркіндік дәрежелер саны деп аталады.

Жалпы жағдайда қалыпты үлестірім параметрлері а, болса, онда алмастыруы арқылы параметрлері (0,1) болатын қалыпты үлестірімге келтіруге болады, яғни

болады. - үлестірімнің кестесі барлық оқулықтарда келтірілген.

2. Стьюдент үлестірім (t – үлестірім).

Айталық параметрлері 0 және болатын тәуелсіз қалыпты үлестіріммен берілген кездейсоқ шамалар болсын. Сонда Стьюдент үлестірімі мына түрде анықталады.

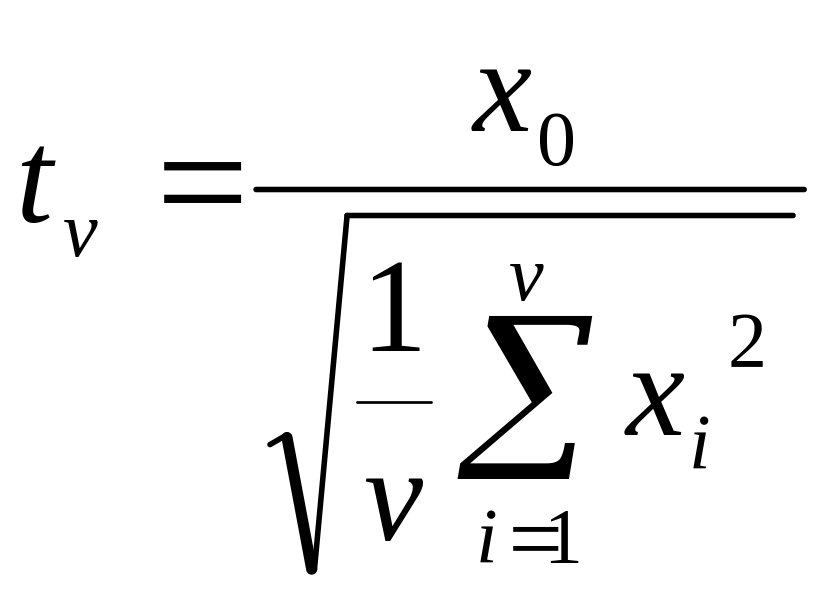
Мұнда v – еркіндік дәрежелер саны.

Егер қалыпты үлестірімнің параметрлері а және болса, онда кездейсоқ шамалары да тәуелсіз болады да, олардың параметрлері сәйкес 0 және болады. Сонда Стьюдент үлестірімі төмендегідей беріледі:

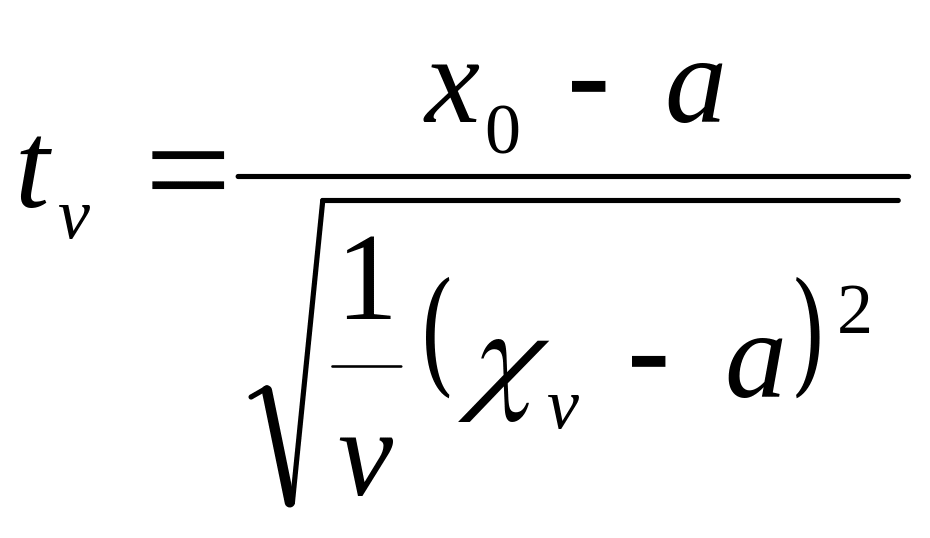Ал а=0, =1 болса, онда Стьюдент үлестірімі

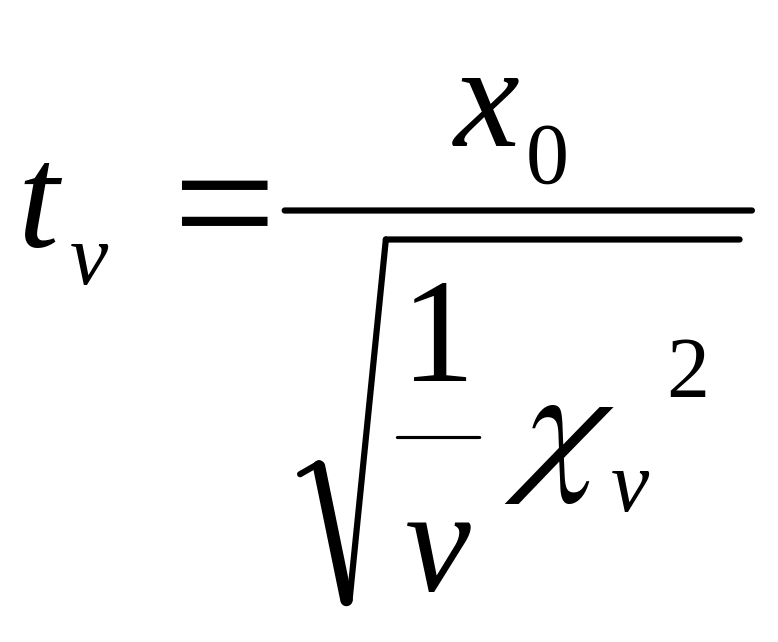
болады, мұндағы жоғарында қарастырылған үлестірімі.

3. Фишер үлестірімі /F – үлестірімі/

Айталық параметрлері (0,о) болатын тәуелсіз қалыпты үлестіріммен берілген кездейсоқ шамалар қарастырылсын:

Сонда мына функция арқылы берілген кездейсоқ шаманы Фишер үлестірімі арқылы берілген деп атайды

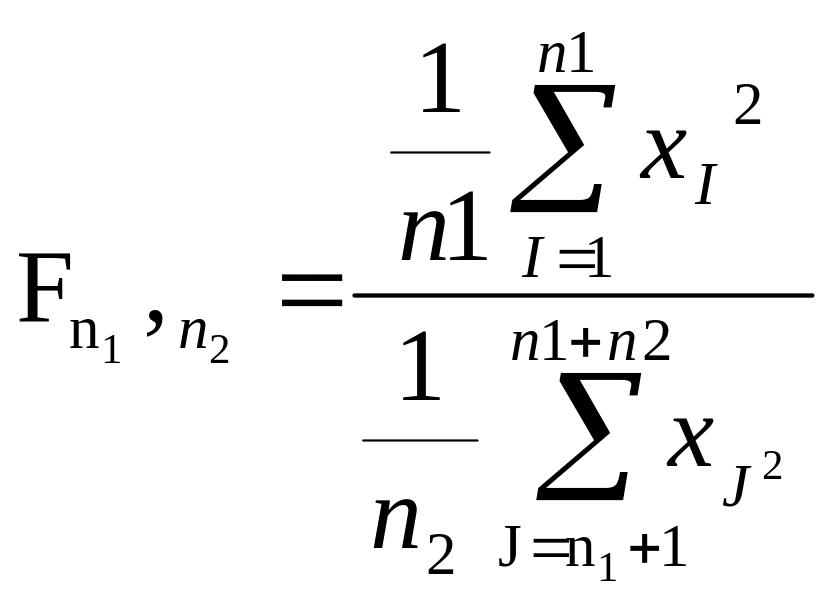
Егер х - кездейсоқ шамалардың параметрлері (а, ) болса; онда Фишер үлестірімі төмендегідей анықталады:

F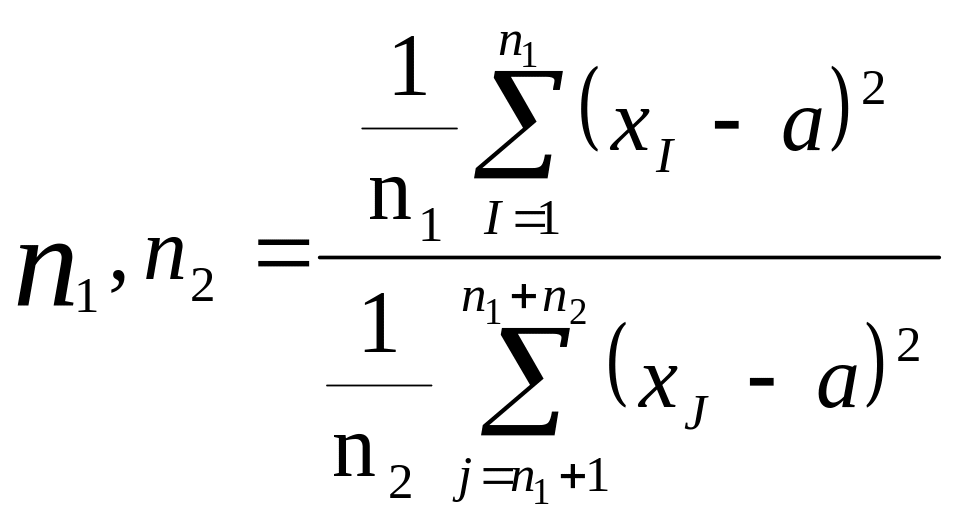

Ал егер а=0, =0 болса, онда Фишер үлестірімі былай жазылады:

Fn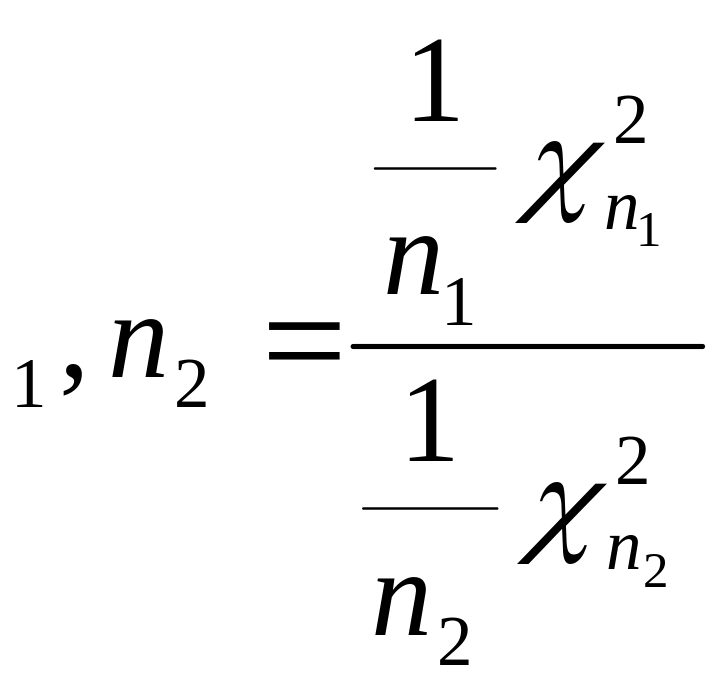

Мұндағы және кездейсоқ шамалары - үлестіріммен берілген.