М.Х.Хамитов

ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ ЖӘНЕ МАТЕМАТИКАЛЫҚ СТАТИСТИКА ЭЛЕМЕНТТЕРІ

Ғылым мен еңбек адамды алыпқа айналдырады.

Қаныш Сатпаев

Практикалық бөлімі Ықтималдықтар теориясына есептер шығару

Кездейсоқ оқиғалар

Бірінші мысал. Қорапта 4ақ,9 қара және 7 қызыл бірдей шарлар салынған. Қораптан кез-келген бір шар алынады.Сонда ақ шар пайда болуының ықтималдылығы қандай?

Шешуі: А-ақ шар пайда болуы болсын.Бұл тәжірибеде элементарлық оқиға дегеніміз қораптан кез-келген бір шар алу.Шарлар бірдей болғандықтан бұл оқиғалар тең мүмкінді және өзара үйлесімсіз. Элементарлық оқиғалардың жалпы саны осы қораптағы шарлар санына тең n=20,ал А оқиғасына қолайлы элементарлық оқиғалар саны қораптағы ақ шарлар санына тең. Сондықтан ықтималдықтың анықтамасы бойынша

Екінші мысал:а:

а) Ө, Н, С, Е, Д, У әріптері бөлек карталарға жазылған. Содан кейін карталар араластырып кез-келген ретпен бір қатарға орналастырылған. Сонда сәндеу сөзінің пайда болуының ықтималдығы қандай?

б) Әрқайсысында бір әріп жазылған карталардан “Жарлық”сөзі құрылған.Карталарды араластырып, содан кейін бір-бірлеп алған ретімен сөз құрастырылады.Сонда ЖАҚ сөзінің пайда болуының ықтималдығы қандай?

Шешуі: а) Берілген алты карталардың бір қатарға әртүрлі орналасуларының бір-бірімен айырмашылығы олардың қандай ретпен орналасқандығында болады.Сондықтан ондай орналасулардың жалпы саны мына формуламен анықталады, яғни

n=

Берілген алты картаның әрбір орналасу комбинацияларын оқиға ретінде қарастырсақ, онда олар тең мүмкінді, үйлесімсіз оқиғалар болады. Ал бізге қолайлы элементарлық оқиғалар саны m=1.

Себебі карталар әртүрлі комбинациямен орналасқанда “Сәндеу” сөзі бір-ақ рет кезігеді.Сонда

б) Берілген алты карталардан үш карта бойынша орналастырулар саны n= . Ал үш әріптен тұратын комбинациялардың бізге керегі біреу-ақ, яғни ЖАҚ, олай болса m=1.Сөитіп

Үшінші мысал. Ұйымда 6 ер адам, 4 әйел адам жұмыс істейді. Табельдегі нөмірлері бойынша 7 адам таңдап алынды. Таңдап алынған адамдардың ішінде 3 әйел бар болуының ықтималдығын табу керек.

Шешуі: Табельдегі нөмірлері бойынша барлығы 10 адамнан 7 адам таңдап алудың жалпы саны 10 элементтен 7 элемент бойынша алынған терулер саны сияқты есептелінеді, яғни

n=

Ал 3 әйелді табельдік нөмерлері бойынша 4 әйелдің ішінен таңдап алудың саны

m =C

Сондай-ақ 6 ер адамнан 4 ер адам таңдаудың саны

m =C

Енді көбейту ережесін пайдалансақ таңдап алынған 7 адамның ішінде 3 әйел 4 ер адам болу мүмліндіктерінің жалпы саны тең.

Сонымен анықталғалы отырған ықтималдық

Бұдан былай ықтималдықтың анықтамасын пайдаланып есептер шығарғанда, әуелі оқиғаны белгілі бір әріп арқылы белгілеп алу қажет. Содан кейін тең мүмкінді, үйлесімсіз элементарлық оқиғалардың жалпы санын, сосын қолайлы элементарлық оқиғалар санын есептеген жөн.

Төртінші мысал: Кітап сөресінде кездейсоқ ретпен 5 томнан тұратын анықтама қойылған:

а) кітаптар бірінші томнан бесінші томға дейін дұрыс ретпен орналасуының ықтималдығын табу керек;

б) ең болмағанда бір томның ретті орнында тұрмаған жағдайдың ықтималдығын табу керек.

Шешуі: Сынақ ретінде кітап сөресінде кітаптардың кез-келген ретпен қойылуын қарастырайық. Сонда кітаптардың бұлай орналасуларының жалпы саны

n=P =5!=120

1) А әріпі арқылы кітап сөресінде кітаптардың том нөмірлерінің өсу ретімен орналасуын білдіретін оқиғаны белгілейік. Бұл оқиғаға қолайлы элементарлық оқиға біреу-ақ.

Сондықтан

P(A)=

2) В әріпі арқылы, ең болмағанда бір том ретті орнында болмауын білдіретін оқиғаны белгілейік. Мұндай оқиғалар саны m=n-1, яғни m=119. Себебі кітаптардың том нөмірлері бойынша дұрыс орналасуы бірге тең, ал қалған орналасулар В оқиғасын анықтайды. Сонымен Р(В)=119/120;

Осы жерде А мен В оқиғаларының қарама-қарсы екенін ескерсек, онда Р(А)+Р( )=1 екенін пайдаланып

Р(В)=1-Р(А)=1- табамыз, яғни бұрынғы жауапты алдық.

Бесінші мысал. Қорапта бірдей 5 бұйым бар. Оның үшеуі боялған. Қораптан кез-келген екі бұйым алынды:

1) алынған екі бұйымның біреуі боялған бұйым болуының ықтималдығын табу керек;

2) алынған бұйымның екеуі де боялған бұйым болуының ықтималдығын табу керек.

Шешуі: 1) қорапта 5 бұйымның екеуін барлығы n=C тәсілмен алуға болады, ал алынған екі бұйымның біреуі боялған болса, сол бір боялған, бір боялмаған бұйымдарды сәйкес m =C m =C тәсілмен алуға болады. Сонда екі бұйымның бірі боялған болудың барлық қолайлы элементарлық оқиғалар саны

Сөйтіп Р=

2) алдыңғы пунктегі шығару жолын пайдаланып

Сонда

Алтыншы мысал. Екі 4 және 5 цифрларының көмегімен әртүрлі үш орынды қанша сан жазуға болады?

Шешуі: Барлығы екі 4 және 5 цифрлары берілгендіктен іздеп отырған комбинацияларды бірден жазуға болады: 444, 445, 454, 544, 555, 554, 545, 544 барлығы 8 сан болады. Ал осы жауапты қайталанбалы орналастыруды пайдаланып та алуға болады.

Жауабы: Барлығы 8 сан жазуға болады.

Жетінші мысал. Мына 5;3;1;5;5;1 цифрлардың көмегімен алты таңбалы қанша сан жазуға болады.

Шешуі: Берілген алты цифрды үш группаға бөлеміз: 1; 1, 3; 5, 5;5.

Есептің шартына қайталанбалы алмастырулар формуласын пайдалануға болады.

Сонда

Жауабы: Барлығы 60 сан жазуға болады.

Сегізінші мысал. Гүл дүкенінде 3 түрлі гүлдер бар. Алынған 7 гүлден қанша әдіспен букет жасауға болады?

Шешуі: Сатып алынған гүл саны 7-ге тең. Сондықтан жасалған букет 7 гүлден тұрады. Ал осы букетке үш түсті гүлдердің әрбір түсінен бірнеше гүл кіруі мүмкін. Олай болса қайталанбалы терулер формуласын пайдаланып

Жауабы: 36 әдіспен букет жасауға болады.

Тоғызыншы мысал. 1-ден 35-ке дейінгі бүтін сандар арқылы нөмірленген 35 емтихан билеттерінің ішінен қалай болса солай бір билет алынған. Суырылған билеттің нөмірі үшке еселі сан болу ықтималдығы қандай?

Шешуі: Тәжірибеміз – бір билет алу. Билет қалай болса солай суырылғандықтан тәжірибенің барлық нәтижелері тең ықтималды және оның үстіне, олар қиылыспайды. Тәжірибенің мүмкін нәтижелерінің саны 35-ке тең. А оқиғасы алынған билеттің нөмірі үшке еселі болатындығын көрсетеді. Бұл оқиғаға тәжірибенің 11 нәтижесі қолайлы болады.

{3;6;…;33}. Демек, ізделінді ықтималдық тең

О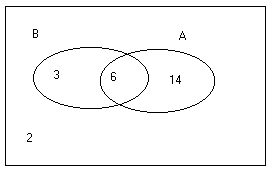 ныншы мысал. Эйлер-Венн диаграммасы.

Группадағы 25 студенттің 20-сы спортсмен, (А оқиғасы), 9-ы музыкамен (Воқиғасы), 6-ы музыкамен және спортпен (АВ оқиғасы). Эйлер-Венн диаграммасын құрып, , , оқиғаларының не білдіретіндігін көрсетелік.

Шешу: Эйлер-Венн диаграммасын құрамыз.Дөңгелектер А мен В оқиғаларын, дөңгелектердің қиылысуы АВ оқиғасын көрсетеді. Дөңгелектердің қиылысуына музыка және спортпен айналысатын студенттердің саны сәйкес келеді, яғни 6 адам. және оқиғалары, бұларға сәйкес, 14 студенттің тек спортсмен, ал 3 студент тек музыкамен айналысатындығын көрсетеді. Демек музыкамен немесе спортпен 23 студент айналысады, сондықтан да оқиғасы студенттердің ішінде тек екеуінің мұндай әуестенуі жоқтығын көрсетеді.