3. Задача по теме «Подобие треугольников».

Билет № 2

1. Определение равных треугольников. Признаки равенства треугольников (доказательство всех признаков).

О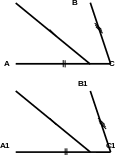 пределение. Треугольники называются равными, если их можно совместить наложением. В таком случае у них попарно равны все соответственные элементы:

АВ = А₁В₁; АС = А₁С₁; ВС = В₁С₁; А = А₁; В = В₁; С = С₁.

Обозначение равенства треугольников: ∆ АВС = ∆ А₁В₁С₁.

При этом имеет значение порядок, в котором записываются вершины треугольника.

Равенство: ∆ АВС = ∆ А₁В₁С₁ означает, что А = А₁; В = В₁; С = С₁.

Соответственно равенство: ∆ АВС = ∆ MNQ означает, что в этих треугольниках А = M; В = N; С = Q.

Существование треугольника, равного данному.

П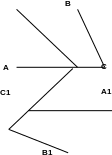 усть есть АВС и луч а. Переместим АВС так, чтобы его вершина А совместилась с началом луча а, вершина В попала на луч а, а вершина С оказалась в заданной полуплоскости относительно луча а. Вершины полученного треугольника обозначим А₁, В₁, C₁. Треугольник А₁В₁С₁ равен треугольнику АВС.

Аксиома о существовании треугольника, равного данному. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Признаки равенства треугольников. Теорема 1 (первый признак равенства треугольников – СУС). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Дано: ∆АВС; ∆А₁В₁С₁; АВ = А₁В₁; A = A₁; АС = А₁С₁.

Доказать: ∆АВС = ∆А₁В₁С₁.

Доказательство:

1. Наложим ∆авс на ∆а1в1с1 так, чтобы точка а совместилась с точкой а1, а стороны ав и ас наложатся соответственно на лучи а1в1 и а1с1.

2. Поскольку АВ = А₁В₁, точки В и В₁ совпадут, а сторона АВ совместится со стороной А₁В₁.

3. Поскольку АС = А₁С₁, точки С и С₁ совпадут, а сторона АС совместится со стороной А₁С₁.

4. Согласно аксиоме существования прямых стороны ВС и В₁С₁ также совпадут. ∆АВС = ∆А₁В₁С₁.

Теорема 2 (второй признак равенства треугольников – УСУ). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Дано: ∆АВС; ∆А₁В₁С₁; A = A₁; АС = А₁С₁; С = С₁.

Доказать: ∆АВС = ∆А₁В₁С₁.

Доказательство:

1. Наложим ∆АВС на ∆А₁В₁С₁ так, чтобы точка А совместилась с точкой А₁, сторона АС – с равной ей стороной А₁С₁, а вершины В и В₁ оказались по одну сторону от прямой А₁С₁.

2. Поскольку A = A₁ и С = С₁, то сторона АВ наложится на луч А₁В₁, а сторона СВ наложится на луч С₁В₁. Вершина В – общая точка сторон АВ и СВ – окажется лежащей на лучах А₁В₁ и С₁В₁, а следовательно, совместится с общей точкой лучей А₁В₁ и С₁В₁, т. е. с точкой В₁. Значит, совместятся стороны АВ и А₁В₁, а также СВ и С₁В₁. Значит, ∆АВС = ∆А₁В₁С₁.

Теорема 3 (третий признак равенства треугольников – ССС). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Д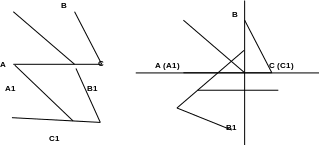 ано: ∆АВС; ∆А₁В₁С₁; АВ = А₁В₁; ВС = В₁С₁; АС = А₁С₁. Доказать: ∆АВС = ∆А₁В₁С₁.

Доказательство: Дополнительное построение. Приложим ∆АВС к ∆А₁В₁С₁ так, чтобы вершина А совместилась с вершиной А₁ и вершина С совместилась с вершиной С₁, а вершина В и вершина В₁ оказались по разные стороны от отрезка АС.