7. Задача по теме «Метод координат».

Билет № 22

4. Теорема косинусов. Следствие из теоремы.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Дано: Треугольник АВС.

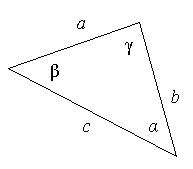Доказать:

1 .;

2. ;

3. .

Доказательство: Возможны три случая:

1. Угол С-острый;

2. угол С- тупой;

3. угол С –прямой.

Докажем первое равенство, два других доказываются аналогично.

;

;

Второй способ решения задачи. Координатный метод.

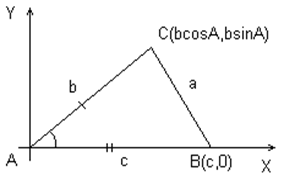
1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату. Решение записывают все учащиеся.
2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). 3. Найдём квадрат стороны BC: BC2 = a2 = (bcosA - c)2 + (bsinA)2 = = b2cos2A – 2bccosA + c2 + b2sin2A = = b2(cos2A + sin2A) + c2 – 2bccosA = = b2 + c2 – 2bccosA.

Вывод: Теорема Пифагора является частным случаем теоремы косинусов.

Рассмотрим следствия из теоремы косинусов.

1 следствие.
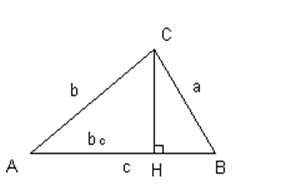
Дано: ABC AC = b, AB = c, AH = bc __________________ Найти: a	Решение: Возможны 2 случая: а)  A – острый, то cosA > 0, б)  A – тупой, то cosA < 0, а) Если  A – острый, тогда по теореме косинусов a2 = b2 + c2 – 2bccosA
	В прямоугольном  ACH: bc = bcosA. Так как  A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой. Случай, когда угол, лежащий против неизвестной стороны тупой ,т.к. cosA < 0, то a2 = b2 + c2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой.
2 следствие.
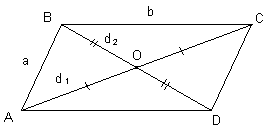
Дано: ABCD – параллелограмм, AB = CD =a, BC = AD = b. __________________ Найти: d12 + d22 .	Решение: ABC: d12 = a2 + b2 – 2abcosB. ABD: d22 = a2 + b2 – 2abcosA = a2 + b2 – 2abcos(180° -  B) = a2 + b2 + 2abcosB. d12 + d22 = a2 + b2 – 2abcosB + a2 + b2 + 2abcosB = a2 + b2 + a2 + b2. d12 + d22 = 2 a2 + 2 b2.
	Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
3 следствие.
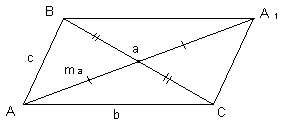
Дано: ABC, AB = c, AC = b, BC = a. __________________ Найти: ma	Решение: Достроим  ABC до параллелограмма ABA1C. AA12 + BC2 = 2b2 + 2c2 . BC = a, 2ma= AA1. (2ma)2 + a2 = 2b2 + 2c2 4ma2 = 2(b2 + c2) – a2 ma2 =    ma =    mb =  mc =
	Вывод: В любом треугольнике со сторонами a, b и c длины медиан ma, mb, mc вычисляются по формулам:ma =  , mb =  , mc =  .

5. Построение прямой, параллельной данной. Построение касательной, проходящей через данную точку, не лежащую на данной окружности.

6. Задача по теме « Подобие».

Билет № 23

4. Теорема об отношении площадей треугольников, имеющих по одному равному углу. Вывод формул площадей треугольника через радиусы вписанной и описанной окружностей.

5. Описанный четырехугольник. Свойство сторон описанного четырехугольника. Формула площади выпуклого четырехугольника . Частный случай, если диагонали взаимно перпендикулярны.

6. Задача по теме «Окружность».

Билет № 24

1. Определение подобных многоугольников. Построение многоугольника, подобного данному. Теоремы об отношении периметров и площадей подобных многоугольников.

2. Неравенство треугольника.

Теорема. В каждом треугольнике любая сторона меньше суммы двух других сторон, но больше их разности.

Д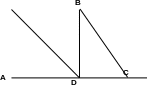 оказательство:

Пусть дан АВС: AB = c, BC = a, AC = b.

AC > AB > BC.

1) Докажем, что AC < AB + BC или b < a + c.

Проведем перпендикуляр BD к стороне AC. Из АВD по теореме о перпендикуляре, проекции и наклонной Аналогично из ВСD Следовательно

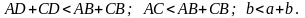
2) Докажем, что AC > AB – BC или b > c – a.

Достаточно заметить, что согласно первой части теоремы c < a + b  b > c – a.

Следствие 1 из неравенства треугольника. Для любых точек А, В, С, не лежащих на одной прямой, имеют место неравенства:

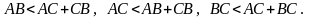
Каждое из этих неравенств называется неравенством треугольника.

Следствие 2 из неравенства треугольника. Во всяком многоугольнике каждая сторона меньше суммы всех других сторон.

Доказательство:

Пусть А₁А₂А₃…A_n – некоторый n-угольник. Тогда из неравенства треугольника:

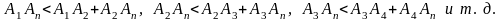
Откуда

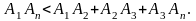
Продолжая эти рассуждения, получим:

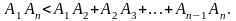
Следствие 3 из неравенства треугольника. Если для трех точек А, В, С выполняется равенство: 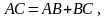то эти три точки лежат на одной прямой, причем точка В лежит между точками А и С.

3. Задача по теме «Элементы треугольника».

Билет № 25

4. Теорема о сумме квадратов диагоналей параллелограмма.

5. Доказать тождества:

.

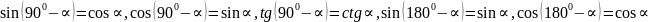6. Задача по теме «Подобие».