2. Построение биссектрисы угла. Доказать свойство биссектрисы треугольника. Теорема об отношении отрезков биссектрисы треугольника, но которые она делится точкой пересечения биссектрис.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

Построение биссектрисы данного угла:

1). Циркулем из вершины угла А проводим дугу произвольного радиуса до пересечения со сторонами угла в точках В и С.

2). Из точек В и С проводим дуги одинакового радиуса до пересечения в точке D.

3). Из точки A через точку D проводим луч AD.

Д окажем, что CAD = BAD.

В ACD и ABD:

AD – общая;

AB = AC – по построению;

CD = BD – по построению.

ACD = ABD (по третьему признаку).

CAD = BAD.

AD – биссектриса.

Теорема о биссектрисе угла треугольника. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные соответствующим боковым сторонам.

Д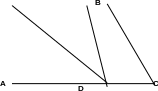 оказательство:

1). Пусть BD – биссектриса угла В в АBС. Она разбивает треугольник на два треугольника: АBD и BСD.

2). По теореме синусов из АBD:

3). По теореме синусов из BСD:

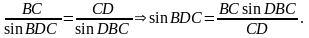
4). АDB + CDB = 180° - смежные 

Следствие 1. Пусть BD – биссектриса угла В треугольника АВС. Тогда отрезки AD и CD находятся по формулам:

Доказательство:

Пусть АС = b, AB = c, BC = a. Если AD = x, то DC = b – x. Составим пропорцию:

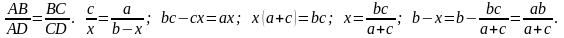
3. Задача по теме «Прямоугольник, квадрат».

Билет № 11

1. Доказать признаки параллелограмма. Построение параллелограмма по двум сторонам и диагонали.

Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.

Д ано: ABCD – четырехугольник; АD II BC, АD = BC.

Доказать: АВСD – параллелограмм.

Доказательство: Проведем диагональ АС. АС – общая; ВС = АD (по условию);ВСА = САD (внутренние накрест лежащие при АD II BC и секущей АС);  АВС = АDС (по 1 признаку).

ВAC = ACD (внутренние накрест лежащие)  АВ II СD. АВСD – параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

Д ано: ABCD – четырехугольник; АВ = СD, АD = BC.

Доказать: АВСD – параллелограмм.

Доказательство: Проведем диагональ АС. АС – общая; ВС = АD (по условию); АВ = СD (по условию);  АВС = АDС (по 3 признаку). ВСА = САD (внутренние накрест лежащие)  АD II BC; ВAC = ACD (внутренние накрест лежащие)  АВ II СD.

АВСD – параллелограмм.

П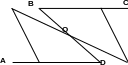 ризнак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

Дано: ABCD – четырехугольник; АС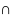 ВD = {О}; BO = OD; AO = OC.

Доказать: АВСD – параллелограмм.

Доказательство: ВO = OD (по условию); АO = OС (по условию); AOВ = СOD (вертикальные);

 АОВ = DОС (по 1 признаку).

ОВА = СDО (внутренние накрест лежащие)  АВ II СD; ВO = OD (по условию); АO = OС (по условию); СOВ = АOD (вертикальные);

 СОВ = DОА (по 1 признаку). ВCО = ОAD (внутренние накрест лежащие)  АD II BC.

АВСD – параллелограмм.