2.Определение окружности. Формулы для вычисления длины окружности(без вывода) и длины дуги окружности.

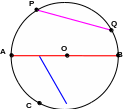О пределение 1. Окружностью называется геометрическая фигура, состоящая из множества точек, равноудаленных от данной точки. Эта точка называется центром окружности. О – центр окружности.

Определение 2. Радиусом окружности называется отрезок, соединяющий любую точку окружности с ее центром, а также длина этого отрезка. ОС, ОА, ОВ – радиусы окружности.

Определение 3. Отрезок, соединяющий две точки окружности, называется хордой. PQ, АВ – хорды.

Определение 4. Наибольшая хорда окружности, проходящая через центр окружности, называется диаметром. Центр окружности является серединой диаметра. Диаметр равен двум радиусам. АВ – диаметр.

Определение 5. Дугой окружности называется часть окружности, ограниченная двумя точками окружности. АС, АP, PQ, ВQ, BC – дуги окружности.

Формула длины окружности. Длина С окружности радиусом R выражается формулой С = 2R.

Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей.

Формула длины дуги окружности). Длина дуги окружности определяется по формуле

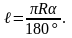
Так как длина окружности С = 2R, то длина дуги в 1° 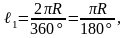а длина дуги в °

3. Задача по теме « Задача на построение».

Билет № 10

1. Определение параллелограмма. Свойства параллелограмма с доказательством (не менее четырех свойств).

Определение 1. Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.

У каждого параллелограмма четыре вершины, четыре стороны, четыре угла. Две стороны, имеющие общие концы, называются смежными. У каждого параллелограмма две диагонали – отрезки, соединяющие противоположные вершины параллелограмма. Сумма углов параллелограмма равна 360°.

Свойства параллелограмма.

Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны.

Доказательство: Проведем диагональ АС. АС – общая; ВАС = АСD (внутренние накрест лежащие при АВ II BC и секущей АС);ВСА = САD (внутренние накрест лежащие при АD II BC и секущей АС); АВС = АDС (по 2 признаку).АВ = CD; BC = AD; В = D.А = ВАС + СAD; С = АСB + АСD;  А = С.

Свойство 2. У параллелограмма углы, прилежащие к одной стороне, в сумме дают 180°.

Доказательство:

В + А =180° (внутренние односторонние при ВС II AD и секущей АB).

B + С =180° (внутренние односторонние при AВ II CD и секущей BC).

D + C =180° (внутренние односторонние при ВС II AD и секущей CD).

A + D =180° (внутренние односторонние при AВ II CD и секущей AD).

Свойство 3. Диагонали параллелограмма точкой пересечения делятся пополам.

Д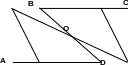 оказательство: Проведем диагонали АС и BD, пересекающиеся в точке О.

АВ = СD (по первому св-ву параллелограмма);

AВO = ODC (внутренние накрест лежащие при АВ II CD и секущей BD);

ВАO = OСD (внутренние накрест лежащие при АB II CD и секущей АС);  АВO = ODС (по 2 признаку).ВO = OD; AO = OC.