15. Разработать алгоритм таксономического анализа для выделения важных признаков. Ваш вариант.

Таксономия. В качестве синонимов для обозначения этой группы методов используют также термины «кластерный анализ», «авто классификация» или (более широко) говорят об использовании методов «распознавания образов». Пусть матрица данных включает характеристики N объектов по двум количественным признакам (например, стаж работы и зарплата). Откладывая признаки по осям координат, мы можем изобразить все объекты на плоскости в виде N точек: абсцисса – значение стажа, ордината – значение зарплаты данного объекта. В этом случае говорят, что N объектов  расположены в двухмерном признаковом пространстве; (по сути, это один из способов изображения двухмерного распределения признаков). Как видно из рисунка, все объекты можно разбить на три группы таким образом, что объекты внутри групп близки между собой (это означает, что они имеют близкие характеристики и по Х и по У), а объекты из разных групп – далеки.

Множество близких между собой точек называется таксоном и при интерпретации результатов рассматривается

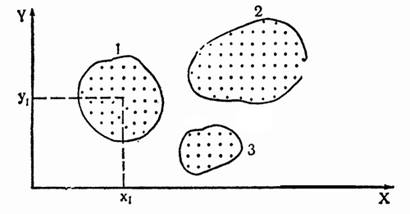
Рис. 28. Изображение объектов в пространстве двух признаков (1, 2, 3 –таксоны)

 

как некоторый социальный тип. Если имеется k признаков, то говорят, что объекты расположены в k-мерном| признаковом пространстве, Если признаков более чем два, то точки уже невозможно изобразить на плоскости. В этом случае группировку можно осуществить с помощью формальных методов, которые и называются методами таксономии.

Результатом работы алгоритмов таксономии обычно является разбиение множества объектов на группы (таксоны) в пространстве признаков, заданных исследователем, а также расчет некоторых обобщенных характеристик каждого из таксонов (центр таксона, средние, меры вариации). Существуют алгоритмы, позволяющие проводить классификацию не только в пространстве признаков, измеренных с помощью метрических шкал, но и для шкал номинальных и порядковых.

6

16. Понятие сходства и задача распознавания.

То, что некоторые вещи обнаруживают между собой сходство или различие, является весьма важным моментом для процесса классификации. Несмотря на кажущуюся простоту, понятие сходства и особенно процедуры, используемые при измерении сходства, не так просты. В самом деле, понятие сходства тесно связано с такими основополагающими эпистемологическими проблемами, как: «Каким образом мы можем образовывать полезные абстрактные понятия, позволяющие внести порядок в то, что мы знаем?». Конечно, чтобы ответить на этот вопрос, нужно уметь рассортировывать вещи по классам, что требует умения объединять вещи, воспринимающиеся как схожие. Проблема сходства состоит, однако, не в простом распознавании сходных или несходных вещей, а в том, какое место эти понятия занимают в научных исследованиях. Наука для плодотворного развития должна базироваться на объективных, воспроизводимых процедурах; таким образом, разработка статистических процедур для измерения более «объективного» сходства вещей является естественным следствием необходимости в воспроизводимых и надежных классификациях.

Количественное оценивание сходства отталкивается от понятия метрики. При этом подходе к сходству события представляются точками координатного пространства, причем замеченные сходства и различия между точками находятся в соответствии с метрическими расстояниями между ними (Tversky, 1977). Размерность пространства определяется числом переменных, использованных для описания событий. Существует четыре стандартных критерия, которым должна удовлетворять мера сходства, чтобы быть метрикой:

1) Симметрия. Даны два объекта х и у; расстояние между ними удовлетворяет условию

2) Неравенство треугольника. Даны три объекта х, у, z; расстояния между ними удовлетворяют условию

Очевидно, это просто утверждение, что длина любой стороны треугольника меньше или равна сумме двух других сторон. Полученное выражение также называется метрическим неравенством.

3) Различимость нетождественных объектов. Даны два объекта х и у:

4) Неразличимость идентичных объектов. Для двух идентичных объектов 

т. е. расстояние между этими объектами равно нулю.

Сформулируем основную задачу распознавания. Пусть заданы множества S, J, P, A_R. Множество S является множеством допустимых объектов, его элементами являются n - мерные векторы, которые называются допустимыми объектами. J – совокупность допустимых начальных информаций. P – множество предикатов, определенное на допустимых объектах,

P={ P₁, P₂,..., P_l}, P_i=P_i (S), i=1, 2,..., l.

Задача распознавания состоит в построении алгоритма для вычисления по информации J значений P₁, P₂,…, P_l для объектов S₁, S₂,…, S_m. Другими словами, алгоритм распознавания A_R переводит набор (J, S₁, S₂,…, S_m) в матрицу где a_ij=P_j(S_i).

Другими словами,

A_R(J(K),I(S)) ={a^A_ij}_mxl, (1.5)

гдеS₁, S₂, …,S_m – допустимые объекты, a_ijÎ{0,1,2}, m³1, J(K) – информация о классах, I(S) – информация об объектах.

Таким образом, основной задачей теории распознавания образов является классификация – отнесение предъявленного объекта к некоторым классам из заданного списка K₁, K₂,…, K_l.

Каждый алгоритм A_R представляется в виде последовательного выполнения алгоритмов B и C.

Алгоритм B применительно к паре (J, S) строит числовую матрицу

B(J, S)= где b_ij– действительные числа. (1.6)

Содержательно, числовое значение элемента B_ij означает оценку или критерий близости объекта S_i к классу K_j.

Алгоритм C по матрице строит матрицу

 

, (1.7)

 

в которой

(1.8)

Алгоритм B называется распознающим оператором, C– решающим правилом алгоритма распознавания.