4.4.Специальные задачи линейного программирования. Задачи целочисленного программирования

Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограни­чения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, если хотя бы одна зави­симость — нелинейная, это будет целочисленная задача нелинейного программирования.

Особый интерес к задачам ЦП вызван тем, что во многих прак­тических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. К их числу относятся:

• задачи оптимизации раскроя;

• оптимальное проектирование машин и оборудования;

• оптимизация системы сервиса и технического обслуживания

машинно-тракторного парка и т.д.

Для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным.

Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программи­рования:

13413\* MERGEFORMAT (.)

Если , то задачу называют полностью целочисленной, если — частично целочисленной.

Существуют различные методы решения задач дискретного программирования (дискретной оптимизации). Наиболее часто используемым методом является метод ветвей и границ. Именно этот метод реализован в программе «Поиск решения» пакета Excel [12].

Дискретная оптимизация средствами Excel проводится анало­гично решению соответствующих непрерывных задач. Основное отличие заключается в том, что в диалоговом окне Поиск решения устанавливается требование целочисленности соответствующих переменных (при этом в режиме Параметры устанавливается тип задачи — линейная или нелинейная).

5. Транспортная задача и ее реализация

Транспортная задача является одной из наиболее распространенных задач линейного программирования и нахо­дит широкое практическое приложение.

Постановка транспортной задачи. Некоторый однородный про­дукт, сосредоточенный у 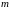поставщиков в количестве единиц, необходимо доставить потребителям в количе­стве единиц. Известна стоимость перевозки единицы груза от поставщика к потребителю . Необходимо план перевозок, позволяющий с минимальными затратами вывести все грузы и полностью удовлетворить потребителей.

Сформулируем экономико-математическую модель транспортной задачи. Обозначим через количество единиц груза, запланиро­ванных к перевозке от поставщика к потребителю . Так как от поставщика к потребителю запланировано перевезти единиц груза, то стоимость перевозки составит .

Транспортная задача относится к двух индексным задачам ли­нейного программирования, так как в результате решения задачи необходимо найти матрицу с компонентами .

Стоимость всего плана выразится двойной суммой

14414\* MERGEFORMAT (.)

Систему ограничений получаем из следующих условий задачи:

1. все грузы должны быть перевезены, т.е.

15415\* MERGEFORMAT (.)

2. все потребности должны быть удовлетворены, т.е.

16416\* MERGEFORMAT (.)

Таким образом, математическая модель транспортной задачи имеет следующий, вид. Найти минимальное значение линейной функции

17417\* MERGEFORMAT (.)

при ограничениях

18418\* MERGEFORMAT (.)

В рассмотренной модели предполагается, что суммарные за­пасы равны суммарным потребностям, т.е.

19419\* MERGEFORMAT (.)

Транспортная задача, в которой суммарные запасы и потреб­ности совпадают, т.е. выполняется условие (4.20), называется за­крытой моделью; в противном случае — открытой.

Для открытой модели может быть два случая:

1. суммарные запасы превышают суммарные потребности:

20420\* MERGEFORMAT (.)

2. суммарные потребности превышают суммарные запасы

21421\* MERGEFORMAT (.)

Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.

Задача заключается в нахождении минимального значения линейной функции

22422\* MERGEFORMAT (.)

при ограничениях в случае (1):

23423\* MERGEFORMAT (.)

при ограничениях в случае (2):

24424\* MERGEFORMAT (.)

Открытая модель решается приведением к закрытой модели.

В случае (1), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель , потребность, которая описывается формулой:

25425\* MERGEFORMAT (.)

Для случая (2), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик запа­сы которого описываются выражением:

26426\* MERGEFORMAT (.)

Стоимость перевозки единицы груза до фиктивного потребителя и стоимость перевозки груза от фиктивного поставщика полагают­ся равными нулю, так как груз в обоих случаях не перевозится.

Транспортная задача состоит из уравнений с неизвест­ными. Матрицу перевозок , удовлетворяющую услови­ям (4.24) – (4.25) называют планом перевозок транспортной задачи, а — перевозками.

План , при котором целевая функция (4.23) обращается в минимум, называется оптимальным [14].