2. C 3 . Решите систему неравенств
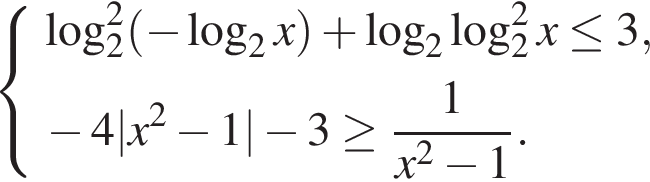
Решение.
Решим
первое неравенство. Из
условия следует, что
и
поэтому
Пусть
Решим
неравенство:
Обратная замена:
Решим
второе неравенство. Учитывая,
что
и,
значит
получаем:
Сделаем
замену
и
получим
откуда,
учитывая, что
находим:
Чтобы найти решение системы, нужно сравнить границы полученных промежутков:
поэтому
Очевидно,
и
Решение системы:
Ответ:
3. C 3 . Решите систему неравенств
Решение.
1.
Решим первое неравенство
системы. Сделаем замену
Тогда
или
откуда
находим решение первого
неравенства системы:
2. Решим второе неравенство системы. Рассмотрим два случая.
Первый
случай:
откуда,
учитывая условие
получаем:
Второй
случай:
Учитывая
условие
получаем:
Решение
второго неравенства
системы:
3.
Поскольку
получаем
решение исходной системы
неравенств.
Ответ:
4. C 3 . Решите неравенство
Решение.
Запишем неравенство в виде:
Сделаем
замену
и
приведем левую часть к общему
знаменателю:
Решением
полученного неравенства
является множество
Возвращаясь
к переменной х,
находим множество решений
исходного неравенства:
Ответ:
5. C 3 . Решите систему неравенств
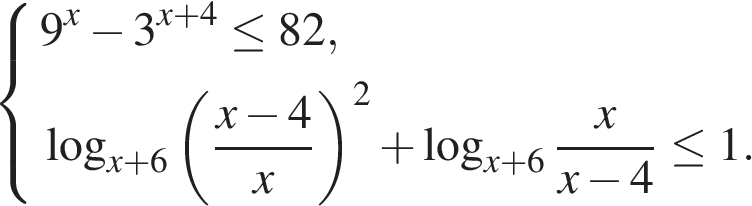
Вариант № 3774962
1. C 3 . Решите систему неравенств:
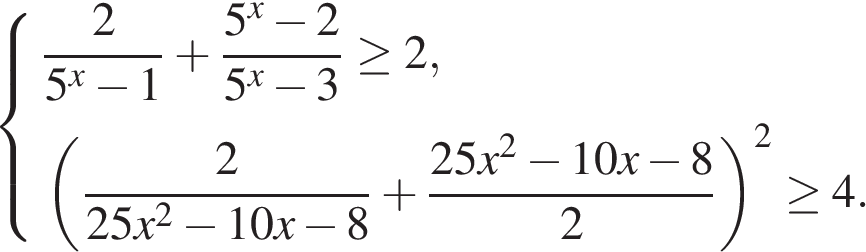
Решение.
Реши
первое неравенство. Сделаем
замену
получаем
Обратная
замена дает
или
Решим
второе неравенство. Сделав
замену
получаем
Значит,
причем
а
Таким образом, получаем решение системы.
Ответ:
2. C 3 . Решите систему неравенств
Решение.
Рассмотрим уравнение . По теореме, обратной теореме Виета, сумма его корней равна , а их произведение равно . Поэтому это числа и . Тогда для первого неравенства системы имеем:
Для решения второго неравенства используем следующие теоремы о знаках: при положительных выражения и имеют одинаковые знаки; для любых для выражения и имеют одинаковые знаки.
Тогда имеем:
Методом интервалов найдем решения: или
Поскольку получаем решение системы.
Ответ:
3. C 3 . Решите систему неравенств
Решение.
Найдем ОДЗ первого неравенства
При
этих значениях переменной
во втором неравенстве:
имеем:
Тогда:
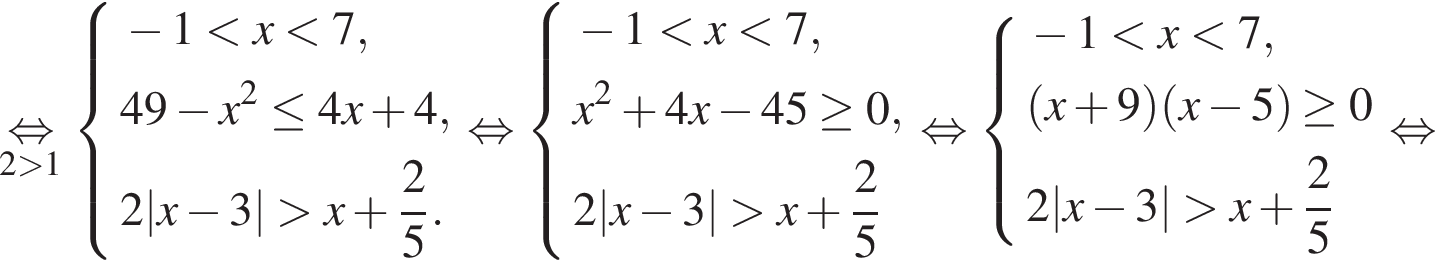
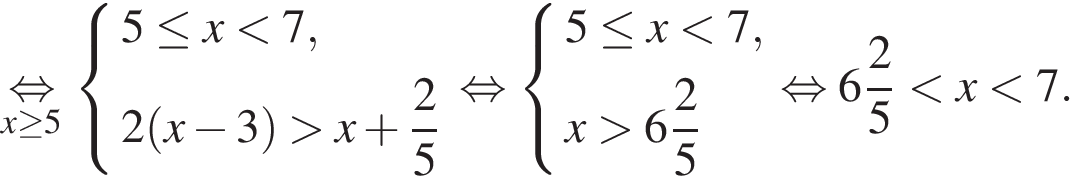
Ответ:
.
4. C 3 . Решите неравенство
Решение.
Заметим, что
1.
и
обращается в ноль только
при
,
то есть и
при
;
2.
при
и
;
3.
при
;
4.
и
при
,
то есть
при
.
Следовательно,
при
имеем:
Откуда
с учетом выколотых точек,
получаем
Ответ:
