Задания С3

Вариант № 3761272

1. C 3 . Ре­ши­те си­сте­му

 

Ре­ше­ние.

Решим пер­вое не­ра­вен­ство

 

 

2. Решим вто­рое не­ра­вен­ство:

 

3. Ре­ше­ни­ем си­сте­мы яв­ля­ет­ся общая часть ре­ше­ний двух не­ра­венств. По­сколь­ку , по­лу­ча­ем.

 

 

 

Ответ: .

2.C 3 .Ре­ши­те си­сте­му не­ра­венств:

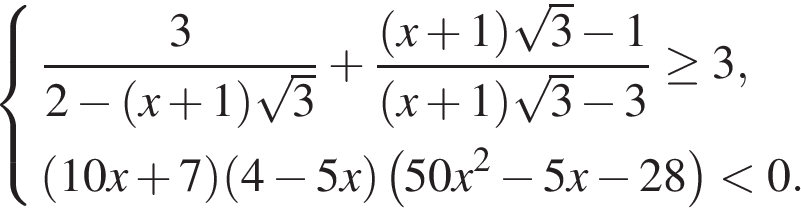
Ре­ше­ние.

Решим пер­вое не­ра­вен­ство. Сде­ла­ем за­ме­ну по­лу­ча­ем

 

или

 

Об­рат­ная за­ме­на дает или

Решим вто­рое не­ра­вен­ство. За­ме­тим, что

 

 

 

по­это­му не­ра­вен­ство вы­пол­не­но при всех , кроме всех и при­чем

 

 

и

 

Таким об­ра­зом, по­лу­ча­ем:

 

 

Ответ:

3. C 3 . Ре­ши­те си­сте­му не­ра­венств

Ре­ше­ние.

Решим пер­вое не­ра­вен­ство:

 

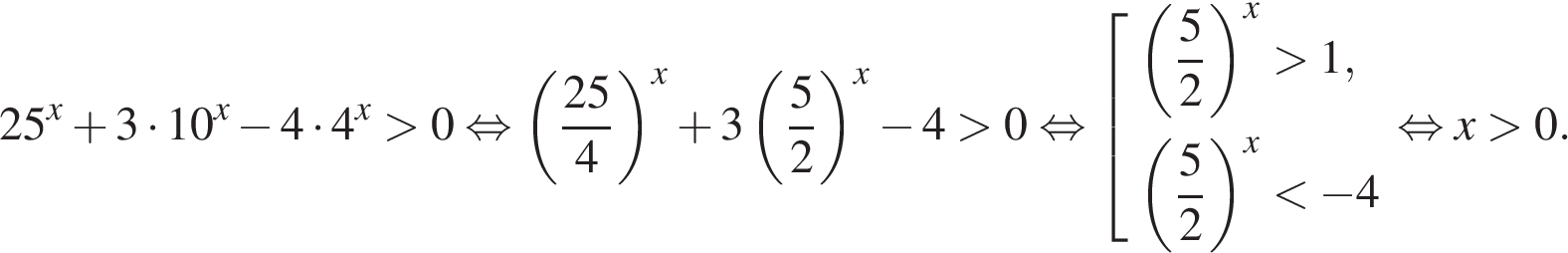
Оста­лось найти по­ло­жи­тель­ные ре­ше­ния вто­ро­го не­ра­вен­ства. За­ме­тим, что вы­ра­же­ние, сто­я­щее под зна­ком ло­га­риф­ма, не мень­ше 1:

 

При по­ло­жи­тель­ных зна­че­ни­ях пе­ре­мен­ной спра­вед­ли­вы не­ра­вен­ства и а зна­чит,

 

и

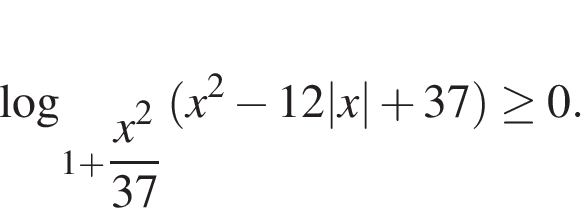
Тем самым, не­ра­вен­ство вы­пол­не­но в том и толь­ко В том слу­чае, когда оба вы­ра­же­ния равны нулю.

Сле­до­ва­тель­но,

 

От­ри­ца­тель­ное ре­ше­ние не­ра­вен­ства не яв­ля­ет­ся ре­ше­ни­ем си­сте­мы.

Ответ:

4. C 3 . Ре­ши­те си­сте­му не­ра­венств

 

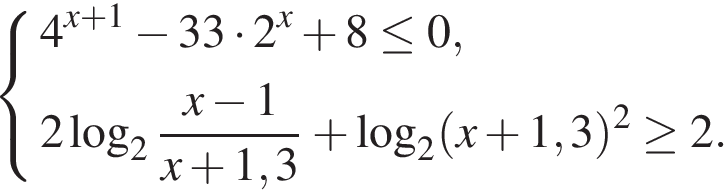
Ре­ше­ние.

Решим пер­вое не­ра­вен­ство. Сде­ла­в за­ме­ну , имеем:

 

 

От­сю­да по­лу­ча­ем ре­ше­ние пер­во­го не­ра­вен­ства:

 

 

Решим вто­рое не­ра­вен­ство. Пер­вое сла­га­е­мое опре­де­ле­но при , вто­рое — при по­это­му об­ласть опре­де­ле­ния вто­ро­го не­ра­вен­ства задаётся не­ра­вен­ства­ми и При этих зна­че­ни­ях пе­ре­мен­ной имеем:

 

 

Учи­ты­вая об­ласть опре­де­ле­ния, по­лу­ча­ем ре­ше­ние вто­ро­го не­ра­вен­ства: или

 

Ре­ше­ни­ем си­сте­мы яв­ля­ет­ся общая часть ре­ше­ний обоих не­ра­венств: или

 

Ответ:

5. C 3 . Ре­ши­те си­сте­му не­ра­венств

Вариант № 3773804

1. C 3 . Ре­ши­те си­сте­му не­ра­венств

Ре­ше­ние.

1. Решим пер­вое не­ра­вен­ство си­сте­мы:

 

 

Рас­смот­рим два слу­чая. Пер­вый слу­чай:

 

нет ре­ше­ний.

 

Вто­рой слу­чай:

 

от­ку­да

 

Ре­ше­ние пер­во­го не­ра­вен­ства ис­ход­ной си­сте­мы:

2. Решим вто­рое не­ра­вен­ство си­сте­мы:

 

 

Ре­ше­ние вто­ро­го не­ра­вен­ства ис­ход­ной си­сте­мы:

3. Ре­ше­ние си­сте­мы не­ра­венств:

 

Ответ:

2. C 3 . Ре­ши­те си­сте­му не­ра­венств

Ре­ше­ние.

1.Решим пер­вое не­ра­вен­ство

 

По­лу­ча­ем:

2. Решим вто­рое не­ра­вен­ство:

 

3. Ре­ше­ни­ем си­сте­мы яв­ля­ет­ся общая часть ре­ше­ний двух не­ра­венств. По­сколь­ку по­лу­ча­ем.

 

Ответ:

3. C 3 . Ре­ши­те си­сте­му не­ра­венств

 

Ре­ше­ние.

1. Решим пер­вое не­ра­вен­ство си­сте­мы. Сде­ла­ем за­ме­ну

 

Учи­ты­вая, что по­лу­ча­ем: от­ку­да на­хо­дим ре­ше­ние пер­во­го не­ра­вен­ства си­сте­мы

2. Решим вто­рое не­ра­вен­ство си­сте­мы:

 

Сде­ла­ем за­ме­ну

 

Тогда или от­ку­да на­хо­дим ре­ше­ние вто­ро­го не­ра­вен­ства си­сте­мы: или

3. По­сколь­ку по­лу­ча­ем ре­ше­ние ис­ход­ной си­сте­мы не­ра­венств.

Ответ: