11.2 Залежності «напруження – деформації» для бетону й арматури

Залежність «напруження–деформації» для бетону рекомендується у вигляді діаграми, зображеної на рис. 48, котра може бути описана дробово-раціональною функцією

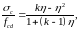(46)

де рівень деформацій, 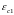– значення відносних деформацій стиску бетону при максимальних напруженнях (при розрахунках за першою групою граничних станів приймається ), .

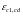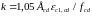Можливе представлення даної залежності у вигляді полінома

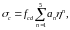(47)

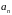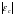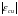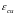де – коефіцієнти полінома, котрі визначаються з використанням параметрів, наведених у нормах. Вирази (46) та (47) справедливі за умови 0< < , де – значення відносних деформацій найбільш стиснутої фібри бетону в момент, коли залізобетонний елемент чинить максимальний опір дії зовнішнього навантаження.

З метою спрощення розрахунку ЗБК, особливо, якщо це призводить до збільшення запасів міцності, можуть бути використані й інші, більш прості, діаграми деформування бетону, наприклад, дволінійна (рис. 49). Величини відносних деформацій для неї визначаються за нормами залежно від класу бетону.

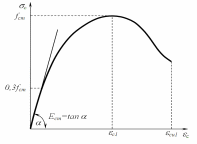
Рисунок 48 – Діаграма механічного стану бетону

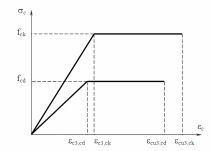
Рисунок 49 – Дволінійна діаграма деформування бетону

У випадку перевірки несучої здатності залізобетонних елементів, які згинаються, з прямокутним або близьким до нього профілем допускається приймати рівномірний за площею стиснутої зони характер розподілу нормальних напружень (рис. 50). Повнота епюри при цьому враховується коефіцієнтом = 0,8.

У якості розрахункової діаграми стану деформування арматури з фізичною межею текучості, котра встановлює зв’язок між напруженнями й її відносними деформаціями, приймають, як правило, дволінійну діаграму (рис. 51).

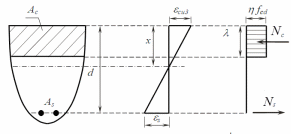
Рисунок 50 – Розрахункова схема нормального перерізу елемента, що згинається, за умови рівномірного розподілення напружень за висотою стиснутої зони

Напруження в арматурі σ_s визначають залежно від відносних деформацій ε_s за формулами:

при , 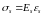; (48)

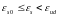при , , (49)

де 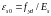– значення відносних деформацій видовження арматури на межі похилої ділянки діаграми (рис. 51), ε_ud – значення відносних граничних деформацій видовження арматури (приймається за нормами).

Існує пропозиція [12], коли зазначена діаграма стану арматури представляється у вигляді рис. 52, при цьому область зміцнення апроксимується параболою

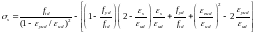, (50)

де ε_yud – деформація наприкінці площадки текучості (точка В), σ_tu, ε_ud – напруження та деформації в точці С максимуму діаграми σ_s – ε_s .

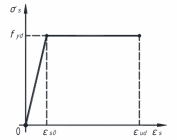
Рисунок 51 – Дволінійна діаграма механічного стану арматури з фізичною межею текучості

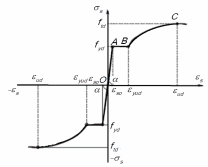
Рисунок 52 – Реальна діаграма механічного стану арматури з фізичною межею текучості

Розглянемо розв’язання задачі міцності для балки прямокутного поперечного перерізу, армованої одиночною арматурою в момент досягнення бетоном на рівні найбільш стиснутої фібри таких значень, коли несуча здатність елемента буде максимальною.

Це можливо здійснювати двома шляхами:

– ε_cu,cd у розрахунках приймається за даними експериментальних досліджень еталонних зразків бетонних призм на стиск залежно тільки від виду та класу бетону (рекомендація норм ε_cu1,cd);

– ε_cu,cd визначається безпосередньо із розрахунку на основі поняття екстремального критерію міцності.

Докладніше зупинимося на другому шляху.