
- •Конспект лекцій
- •Короткий історичний нарис виникнення залізобетонних конструкцій
- •1.3 Властивості та галузі застосування залізобетонних конструкцій
- •1.4 Поняття про попередньо напружені конструкції
- •Лекція №2
- •Класифікація залізобетонних конструкцій за напруженим станом і призначенням. Види збк за способом їх спорудження
- •2.2 Матеріали для кам’яних і армокам’яних конструкцій. Частини будинків і споруд, які виконують із каменю
- •Матеріали для залізобетонних і кам’яних конструкцій та їх фізико-механічні властивості Лекція № 3 фізичні властивості, міцність бетону
- •3.1 Види бетону. Структура бетону та її вплив на міцність і деформативність
- •3.2 Міцність бетону
- •Лекція №4 деформативність бетону
- •4.1 Несилові деформації бетону
- •4.2 Силові деформації бетону
- •Лекція №5 арматура для залізобетонних конструкцій
- •5.1 Види арматури за призначенням
- •5.2 Фізико-механічні властивості арматурної сталі
- •5.3 Класифікація арматури
- •5.4 Арматурні вироби
- •5.5 Стики й перетини арматури
- •Лекція №6 фізико-механічні властивості залізобетону
- •6.1 Усадка та повзучість залізобетону
- •6.2 Зчеплення арматури з бетоном
- •6.3 Анкерування арматури
- •6.4 Захисний шар бетону
- •6.5 Корозія залізобетону
- •Лекція №7 кам'яна та армокам'яна кладка
- •7.1 Міцнісні характеристики кам'яної кладки
- •7.2 Деформативність кладки
- •7.3 Армування кладки
- •Загальні положення про розрахунок будівельних конструкцій Лекція № 8 методи розрахунку за допустимими напруженнями та руйнівними зусиллями
- •8.1 Види та етапи розрахунків, їх завдання
- •8.2 Поняття про стадії напружено-деформованого стану залізобетонних елементів
- •8.3 Основні положення методу розрахунку збк за допустимими напруженнями
- •8.4 Основні положення методу розрахунку збк за руйнівними зусиллями
- •Лекція № 9 основні положення методу розрахунку за граничними станами
- •9.1 Суть методу
- •9.2 Характеристичні та розрахункові значення навантажень. Сполучення навантажень
- •9.3 Характеристичні та розрахункові значення опорів матеріалів
- •9.4 Коефіцієнти надійності за відповідальністю
- •9.5 Суть розрахунку за граничними станами
- •Основи проектування (розрахунку і конструювання) залізобетонних і кам'яних конструкцій Лекція №10 розрахунок міцності згинальних елементів за нормальНиМи перерізами згідно сніп [8]
- •10.1 Передумови розрахунку
- •Лекція №11 розрахунок міцності згинальних елементів за нормальними перерізами згідно дбн [10, 11]
- •11.1 Недоліки розрахунку міцності за сНіП
- •11.2 Залежності «напруження – деформації» для бетону й арматури
- •11.3 Розрахунок елементів прямокутного профілю з одиничним армуванням
- •Лекція № 12
- •12.1 Розрахунок елементів прямокутного перерізу з подвійним армуванням
- •12.3 Конструктивні вимоги до армування елементів, що згинаються
- •Лекція №13 розрахунок міцності згинальних елементів за похилими перерізами
- •13.1 Можливі випадки руйнування похилого перерізу
- •13.2 Еволюція методів розрахунку похилого перерізу
- •Розрахунок похилих перерізів на дію згинального моменту [8]. Умову міцності похилих перерізів за згинальним моментом (рис. 57, б)записують як
- •Міцність похилої стиснутої смуги[8]. Експериментально встановлено, що додержання умови
- •13.3 Розрахунок несучої здатності залізобетонних перерізів, похилих до поздовжньої осі згідно дбн [10, 11]
- •Лекція №14 розрахунок міцності залізобетонних елементів прямокутного поперечного перерізу при стиску
- •14.1 Правила проектування
- •Лекція №15 розрахунок елементів кам'яних конструкцій
- •15.1 Стіни із неармованої кам'яної кладки при дії вертикальних навантажень.
- •15.1 Стіни із неармованої кам'яної кладки при дії вертикальних навантажень
- •15.2 Кам'яні стіни при зосереджених навантаженнях
- •15.3 Кам'яні стіни при зсувних і горизонтальних навантаженнях
- •Список літератури
9.5 Суть розрахунку за граничними станами
Умова, що забезпечує несучу здатність конструкцій, тобто неможливість реалізації граничних станів першої групи в загальному вигляді, записується як
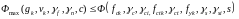 ,
(35)
,
(35)
де Фmax розрахункове зусилля; Ф розрахункова несуча здатність; с розрахункова схема конструкції (елемента); s форма та розміри перерізу.
Це ж рівняння можна записати у скороченому вигляді як
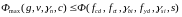 .
(36)
.
(36)
Умови для розрахунку тріщиностійкості в загальному вигляді можна записати залежно від того, чи допускається у конструкції утворення тріщин:
– у випадку, коли тріщини не допускаються, в розрахунках за їх утворенням (для елементів, що згинаються) повинна виконуватися умова
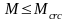 ,
(37)
,
(37)
де М максимальний момент від зовнішнього навантаження; Мcrc момент тріщиноутворення (момент, при якому можлива поява тріщин у конструкції);
– у випадку, коли тріщини обмеженої ширини допускаються, тобто при розрахунках за розкриттям тріщин
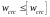 ,
(38)
,
(38)
де wcrc найбільша ширина розкриття тріщин, обчислена теоретично; wcrc граничне значення ширини розкриття тріщин, призначене нормами.
Умову розрахунку за деформаціями маємо у вигляді
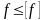 ,
(39)
,
(39)
де f деформація, обчислена теоретично; f граничне значення деформацій, призначене нормами.
Основна перевага методу розрахунку за граничними станами полягає в тому, що введення системи розрахункових коефіцієнтів дає можливість більш диференційовано оцінювати вплив усіх визначальних факторів на роботу конструкцій, а отже, точніше відображати її дійсний напружений стан.
Основи проектування (розрахунку і конструювання) залізобетонних і кам'яних конструкцій Лекція №10 розрахунок міцності згинальних елементів за нормальНиМи перерізами згідно сніп [8]
10.1 Передумови розрахунку.
10.2 Розрахунок елементів прямокутного профілю з одиничним армуванням.
Література: [1], С. 103 ‒ 115, 135 ‒ 142.
Для залізобетонної однопролітної балки, що вільно лежить на двох опорах і завантажена зосередженими силами (або рівномірно розподіленим навантаженням), можливі два види руйнування:
– за перерізом, нормальним до поздовжньої осі елемента, в якому діє максимальний згинальний момент;
– за похилим до поздовжньої осі елемента перерізом, тут діють згинальний момент М і поперечна сила V.
Відповідно до цього розрахунок міцності елементів, що працюють на згинання, виконують окремо для перерізів, нормальних і похилих до поздовжньої осі елемента.
10.1 Передумови розрахунку
В основу розрахунку міцності елементів, що згинаються, за нормальним перерізом покладена ІІІ стадія НДС. При цьому можливі два випадки руйнування.
Випадок 1. При відносно малих відсотках армування руйнування починається, коли напруження в розтягнутій арматурі досягають граничних значень розрахункового опору арматури при розтязі fyd. Це приводить до надмірного розкриття та розвитку за висотою нормальних тріщин, зменшення висоти стиснутої зони бетону й надалі її руйнування при напруженнях, які досягають розрахункового опору бетону стиску fcd. Таке руйнування характерне для непереармованих залізобетонних елементів, його називають пластичним.
Випадок
2.
При значних відсотках армування
руйнування починається зі стиснутої
зони бетону, коли напруження у розтягнутій
арматурі менше від граничних
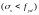 .
Воно властиве для переармованих ЗБК,
його називають крихким
і
слід уникати.
.
Воно властиве для переармованих ЗБК,
його називають крихким
і
слід уникати.
Розмежуванням для можливих випадків руйнування згідно [8] є дотримання умови
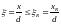 ,
(38)
,
(38)
де
відносна, а х
висота стиснутої зони бетону; R
гранична відносна;
xR
гранична висота стиснутої зони бетону;
d
робоча висота перерізу (відстань від
центру ваги розтягнутої арматури до
найбільш стиснутого бетонного волокна)
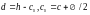 (с
захисний шар бетону, Ø
діаметр поздовжньої робочої арматури).
(с
захисний шар бетону, Ø
діаметр поздовжньої робочої арматури).
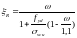 ,
(39)
,
(39)
де характеристика стиснутої зони бетону (може розглядатися як коефіцієнт повноти фактичної епюри напружень у бетоні при заміні її умовною прямокутною епюрою), котру визначають як
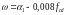 ,
,
тут 1 коефіцієнт, що залежить від виду бетону (для важкого бетону 0,85); scu граничні напруження в арматурі стиснутої зони, котрі при c2 1 дорівнюють 400 МПа, а для елементів при c 2 1 500 МПа.
За значеннями та R установлюють випадок руйнування. При R переріз є непереармованим і руйнування при відповідному навантаженні може відбуватися за випадком 1. При > R переріз переармований та руйнування відбувається за випадком 2.
Міцність елементів, що згинаються, за нормальним перерізом визначають із розгляду напруженого стану перерізів, які руйнуються за схемою 1-ого випадку. При цьому:
– роботу бетону розтягнутої зони не враховують;
– напруження
в розтягнутій арматурі досягають значень
розрахункового опору розтягу
fyd,
у
стиснутій
розрахункового опору стискові
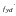 ;
;
– опір бетону стисканню приймається рівномірно розподіленим за висотою стиснутої зони (прямокутна епюра) таким, що дорівнює fcd;
– розрахункові формули виводять із умов рівноваги перерізу, в якому діє згинальний момент від зовнішнього розрахункового навантаження М та внутрішні зусилля в стиснутій зоні бетону й усій поздовжній арматурі.
10.2 Розрахунок елементів прямокутного профілю з одиничним армуванням
В елементах, що згинаються, арматуру доцільно встановлювати в розтягнутій зоні. Армування стиснутої зони проводять лише за необхідності її підсилення, котру встановлюють розрахунком. Спочатку передбачають, що арматура в стиснутій зоні не потрібна (в більшості випадків так воно і виявляється) й виконують розрахунок, виходячи з одиночного армування. Умова рівності нулю суми проекцій усіх нормальних зусиль на поздовжню вісь елемента має вигляд
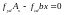 .
(40)
.
(40)
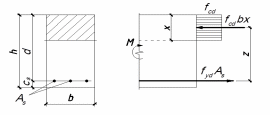
Рисунок 47 – Розрахункова схема нормального перерізу при розрахунках міцності прямокутних елементів з одиночним армуванням
Міцність елементів за нормальним перерізом забезпечена, якщо згинальний момент від зовнішніх розрахункових зусиль М не перевищує розрахункової несучої здатності того самого перерізу за згинальним моментом Мu (розрахунковий момент, який може витримати переріз при досягненні ним граничного стану), тобто
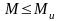 .
.
Величину згинальних моментів визначають відносно осі, що нормальна до площини згину та проходить через точку прикладання рівнодійної зусиль у розтягнутій арматурі (умовно центр ваги розтягнутої арматури)
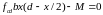 ,
(41)
,
(41)
або стиснутому бетоні (умовно центр ваги стиснутої зони бетону)
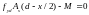 .
(42)
.
(42)
Положення
нейтральної осі (значення х)
знаходять із рівняння (39).
Для полегшення
розрахунків і можливості табулювання
величин формули
(40) – (42) можна
перетворити, використовуючи поняття
відносної висоти стиснутої зони
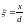 та позначивши через
та позначивши через
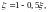
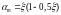
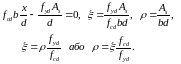 (43)
(43)
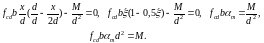 (44)
(44)
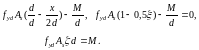 (45)
(45)
Максимальний
відсоток армування елементів, які
працюють на згинання,
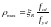 збільшується з підвищенням міцності
бетону та зменшується з підвищенням
міцності сталі. При ρ
> ρmax,
що відповідає
> R,
переріз переармований. Максимальні
відсотки армування залізобетонних
елементів, які працюють на згинання,
для бетонів класів С10/12,5 – С25/30 і сталі
А400С та В500 становлять 1,3 – 3,2 %. Максимально
допустиме насичення арматурою в
залізобетонних елементах застосовують
порівняно рідко, оскільки це збільшує
витрати сталі на конструкцію. Із умови
мінімальної вартості конструкцій
оптимальні відсотки армування та
відповідні їм значення відносної висоти
стиснутої зони приймають: для балок ρ
%
= 1 – 2 % (
=
0,3 – 0,4), для плит
0,5 – 0,7 % (
=
0,1 – 0,15).
збільшується з підвищенням міцності
бетону та зменшується з підвищенням
міцності сталі. При ρ
> ρmax,
що відповідає
> R,
переріз переармований. Максимальні
відсотки армування залізобетонних
елементів, які працюють на згинання,
для бетонів класів С10/12,5 – С25/30 і сталі
А400С та В500 становлять 1,3 – 3,2 %. Максимально
допустиме насичення арматурою в
залізобетонних елементах застосовують
порівняно рідко, оскільки це збільшує
витрати сталі на конструкцію. Із умови
мінімальної вартості конструкцій
оптимальні відсотки армування та
відповідні їм значення відносної висоти
стиснутої зони приймають: для балок ρ
%
= 1 – 2 % (
=
0,3 – 0,4), для плит
0,5 – 0,7 % (
=
0,1 – 0,15).
Згідно з вимогами [8] мінімальний відсоток армування залізобетонних елементів при згині має становити 0,05 %.
При розв'язанні задач міцності можливі різні варіанти.
До задачі першого типу належить перевірка міцності елементів за нормальними перерізами. При цьому задано розміри поперечного перерізу, армування, характеристики міцності матеріалів та згинальний момент від зовнішнього навантаження.
Дано: b, h, fcd,, As, fyd, M.
Перевірка міцності полягає у порівнянні М і Мu.
Розрахунки виконуються у такій послідовності:
– знаходять
висоту стиснутої зони бетону
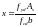 або
або
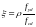 ;
;
– перевіряють
умову
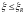 ;
;
– визначають Mu:
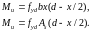
Можна визначати момент, попередньо знайшовши в таблиці [9] за , m:
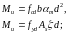
– перевіряють умову . За її виконання міцність можна вважати забезпеченою.
Задача другого типу – підбір перерізу поздовжньої робочої арматури.
Дано: b, h, fcd, fyd, M.
Знайти As.
Розрахунок виконується у такій послідовності:
– знаходять
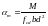 ;
;
– за m , ;
– перевіряють умову ;
– визначають
площу арматури
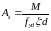 ;
;
– здійснюють конструювання перерізу.
Задача третього типу – підбір перерізів бетону й арматури одночасно.
Дано: fcd , fyd, M.
Визначити: b, h, As.
Послідовність розрахунку наступна:
– задаються оптимальним коефіцієнтом армування ρ та визначають відносну висоту стиснутої зони бетону ;
– за m;
– призначають b;
– знаходять
робочу висоту перерізу
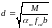 ;
;
– підраховують
загальну висоту перерізу
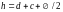 ;
;
– уточнюють ;
– за m , ;
– перевіряють
умову
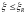 ;
;
– визначають
площу поздовжньої робочої арматури
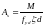 .
.
– здійснюють конструювання перерізу.
