81

3.8.1Расчёт избирательной системы тракта пч с двухконтурными полосовыми фильтрами

Аналитический метод расчёта достаточно сложен, поэтому чаще применяется более простой и наглядный метод расчёта по графикам семейства обобщённых резонансных кривых. Обобщённые резонансные кривые полосового фильтра, содержащего два связанных одинаковых контура приведены на рисунке 2 и в приложении А [3]. На вертикальной оси отложено ослабление , а на горизонтальной – значения обобщённой расстройки

,

где - эквивалентная добротность каждого из контуров фильтра;

- абсолютная расстройка;

- средняя частота полосы пропускания фильтра.

Резонансные кривые построены для различных значений фактора связи , где - коэффициент связи контуров. При значениях резонансные кривые имеют одну вершину, при >1 – две. Применение полосовых фильтров с двухвершинной резонансной кривой усложняет процедуру настройки АЧХ тракта. Поэтому целесообразно попытаться получить требуемые параметры избирательной системы с одной вершиной при факторе связи =1 (критическая связь), которому соответствует максимум коэффициента передачи полосового фильтра на частоте .

Для трактов с ЧМ оптимальное значение с точки зрения лучшей линейности фазовой характеристики составляет 0,7 – 1 [11, 12].

Порядок расчета

1. Задаёмся числом двухконтурных полосовых фильтров , беря их на один больше предполагаемого числа каскадов тракта ПЧ.

Рекомендуется начинать расчет с =3, но не более =4÷5, большее число фильтров и каскадов неоправдано для радиовещательного приёмника из конструктивных, технологических и экономических соображений.

Задаёмся также величиной фактора связи, первоначально рекомендуется принять η=1.

2. Избирательность, которую должен обеспечить один фильтр

, (65)

где – избирательность по соседнему каналу из ТЗ, дБ.

3. Допустимое ослабление на краях полосы пропускания для одного фильтра

, (66)

где – ослабление на краях сквозной полосы пропускания, принятое для тракта ПЧ в п.3.5, дБ.

4. По резонансной кривой с выбранным (рисунок 2) определяем значения обобщенных раскроек , , соответствующие ослаблениям , .

5. Необходимая добротность контуров фильтра, обеспечивающая избирательность

, (67)

где - абсолютная расстройка соседнего канала, при которой задана избирательность, кГц;

- промежуточная частота, кГц.

Для трактов с АМ , для трактов с ЧМ , в формуле (67) нужно использовать положительное значение .

6. Допустимая добротность контуров фильтра, при которой ослабление на краях полосы пропускания составляет

, (68)

где – сквозная полоса пропускания радиотракта по п.3.2, кГц.

7. Наибольшее значение эквивалентной добротности контуров полосового фильтра, которую можно реализовать с учётом шунтирующего действия входной и выходной проводимостей транзисторов УПЧ и смесителя

, (69)

где – коэффициент шунтирования контура транзистором;

- конструктивная добротность контура.

Ориентировочные значения величин и для контуров тракта ПЧ приведены в таблице 8

Таблица 8

Промежуточная частота , МГц	Значения конструктивной добротности для контуров тракта ПЧ	Коэффициент шунтирования
		БТ	ПТ
0,3 и ниже	80 – 250	0,5 – 0,8	0,9 – 1
0,3 – 3	100 – 300	0,5 – 0,8	0,9 – 1
3 – 30	100 – 200	0,5 – 0,8	0,8 – 0,9
30 – 60	50 – 150	0,5 – 0,8	0,5 – 0,8

При выборе значения коэффициента шунтирования следует иметь в виду, что он не только задаёт эквивалентную добротность контуров, но также оказывает влияние на другие параметры тракта. Так при меньшем может быть получено большее усиление в каскаде УПЧ, при большем – большая стабильность АЧХ.

8. В результате расчёта добротностей по пп.5 – 7 необходимо выполнить два условия:

1) < , (70)

2) . (71)

При невыполнении условия 1) нужно выбрать резонансную кривую с >1, у которой провал на средней частоте полосы пропускания (при =0,1) и повторить расчёт по пп.4 – 6. Если увеличивать нежелательно, например для тракта с ЧМ, то можно попытаться выполнить условие 1), увеличивая число полосовых фильтров с соответствующим пересчётом по пп.2 – 6. В крайнем случае можно использовать обе меры одновременно.

При невыполнении условия 2) нужно последовательно провести следующие действия до получения положительного эффекта:

• взять большие значения и из таблицы 8 и пересчитать в п.7;

• выбрать резонансную кривую с <1 и повторить расчёт по пп.4 – 6. Использовать резонансные кривые с <0,5 нежелательно из-за существенного уменьшения коэффициента передачи полосового фильтра;

• увеличить число полосовых фильтров и повторить расчёт по пп.2 – 6.

При выполнении условий 1) и 2) нужно выбрать эквивалентную добротность контуров фильтра , соблюдая условия

3) , . (72)

9. Для принятых значений , и определяем фактические значения:

1. обобщённых расстроек

, (73)

; (74)

2. ослабленный , по кривой с принятым (рисунок 2) для расстроек по п. а);

3. избирательности по соседнему каналу тракта ПЧ

; (75)

4. ослабления на краях сквозной полосы пропускания, вносимого трактом ПЧ

. (76)

Полученные значения и необходимо сравнить с заданными и сделать вывод о выполнении поставленных требований.

10. Если принятое для тракта ПЧ с АМ значение >1, то необходимо скорректировать распределение частотных искажений в таблице 2 (п.3.5) с учётом провала АЧХ на средней частоте полосы пропускания. При этом

, (77)

где - фактическое значение провала на средней частоте полосы пропускания одного полосового фильтра, определяется по резонансной кривой с принятым значением (рисунок 2) при =0,1.

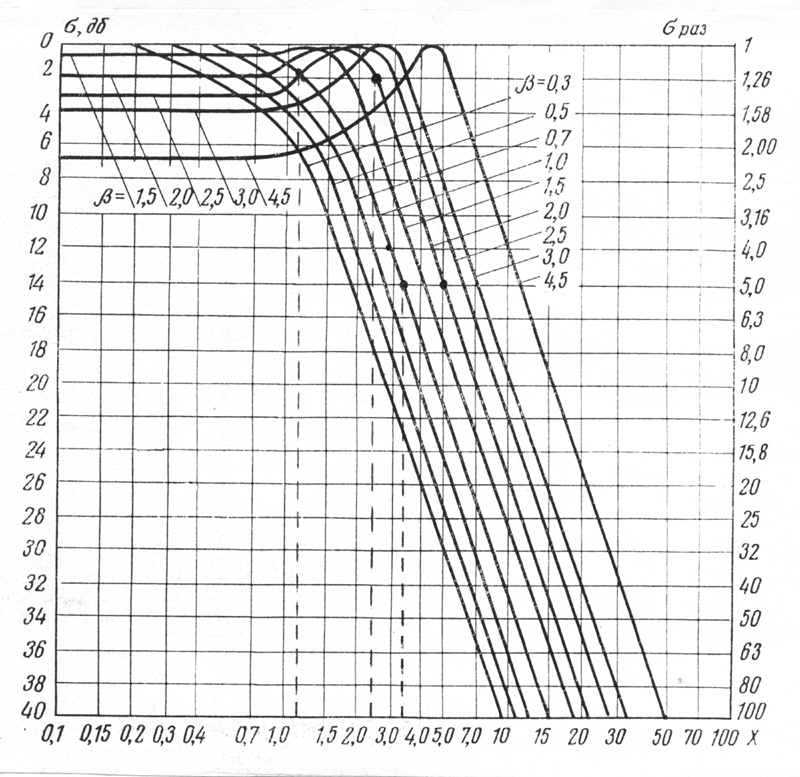
Рисунок 2 – обобщённые резонансные кривые полосового фильтра

Пример 8. Определить основные параметры избирательной системы тракта ПЧ с двухконтурными полосовыми фильтрами для приёмника АМ сигналов.

Исходные данные:

• промежуточная частота =465кГц;

• полоса пропускания радиотракта по п.3.2 =8кГц;

• избирательность по соседнему каналу из ТЗ =56дБ;

• ослабление на краях сквозной полосы пропускания, принятое для тракта ПЧ в п.3.5 =8дБ;

• абсолютная расстройка соседнего канала =±9кГц;

• в тракте ПЧ предполагается использовать БТ.

Расчёт

1. Задаёмся числом двухконтурных полосовых фильтров =4, т.к. нужно обеспечить высокую избирательность по соседнему каналу =56дБ. Принимаем первоначально фактор связи =1.

2. Избирательность, которую должен обеспечить один фильтр по формуле (65)

.

3. Допустимое ослабление на краях полосы пропускания для одного фильтра по формуле(66)

.

4. По резонансной кривой с =1 (рисунок 2) определяем значения обобщённых расстроек и , соответствующие ослаблениям и :

=14дБ =3,2,

=2дБ =1,2.

5. Необходимая добротность контуров фильтра, обеспечивающая избирательность по формуле (67)

.

6. Допустимая добротность контуров фильтра, при которой ослабление на краях полосы пропускания составляет по формуле (68)

.

7. Наибольшее значение эквивалентной добротности контуров полосового фильтра, которую можно реализовать с учётом шунтирующего действия входной и выходной проводимостей транзисторов УПЧ и смесителя по формуле (69)

,

где – коэффициент шунтирования контура транзистором, по таблице 8 для БТ выбираем =0,6;

– конструктивная добротность контура, по таблице 8 выбираем =250.

8. В результате расчёта добротностей по пп.5 – 7 необходимо выполнить два условия (70), (71)

1) < ,

2) .

Условие 1) не выполняется =82,7 > =69,8.

Выбираем другую резонансную кривую с =2>1, у которой провал на средней частоте полосы пропускания (при =0,1) = =2дБ.

Повторяем расчёт по пп.4 – 6.

Определяем значения обобщённых расстроек по резонансной кривой с =2:

=14дБ =5,0,

=2дБ =2,4.

Находим добротности контуров:

,

.

Проводим проверку выполнения условий 1) и 2):

1) =129 < =140,

2) =129 < =150.

Условия 1) и 2) выполняются, тогда выбираем эквивалентную добротность контуров фильтра соблюдая условия 3) (72)

3) , .

Принимаем =135.

9. Для принятых значений =4, =2, =135 определяем фактические значения:

1. обобщённых расстроек по формулам (73), (74)

,

;

2. ослаблений , по кривой с =2 (рисунок 2) для расстроек по п.а)

≈5,2 =15дБ,

≈2,3 =1,7дБ;

3. избирательности по соседнему каналу по формуле (75)

= · =15·4=60дБ;

4. ослабления на краях сквозной полосы пропускания по формуле (76)

= · =1,7·4=6,8дБ.

В результате расчёта получили, что тракт ПЧ должен содержать число двухконтурных полосовых фильтров =4 с фактором связи =2 и эквивалентной добротностью контуров =135.

При этом он обеспечивает:

• избирательность по соседнему каналу =60дБ, что больше заданной в ТЗ (56дБ);

• ослабление на краях сквозной полосы пропускания 6,8дБ, что меньше принятого значения для тракта ПЧ в п.3.5 (8дБ).

10. Поскольку принятое значение фактора связи =2>1, то необходимо скорректировать распределение частотных искажений в таблице 2 (п.3.5) с учётом провала АЧХ на средней частоте полосы пропускания по формуле (77)

· =2·4=8дБ,

где =2дБ – фактическое значение провала на средней частоте полосы пропускания одного полосового фильтра, для резонансной кривой с принятым значением =2 (рисунок 2) при =0,1.

Пример 9. Определить основные параметры избирательной системы тракта ПЧ с двухконтурными полосовыми фильтрами для приёмника ЧМ сигналов.

Исходные данные:

• промежуточная частота =10,7 МГц;

• полоса пропускания радиотракта по п. 3.2 =180 кГц;

• избирательность по соседнему каналу из ТЗ =36 дБ;

• ослабление на краях сквозной полосы пропускания, принятое для тракта ПЧ в п. 3.5 =6дБ;

• абсолютная расстройка соседнего канала =±300 кГц;

• в тракте ПЧ предполагается использовать БТ.

Расчёт

1. Задаёмся числом двухконтурных полосовых фильтров =3, а также величиной фактора связи =1.

2. Избирательность, которую должен обеспечить один фильтр по формуле (65)

дБ.

3. Допустимое ослабление на краях полосы пропускания для одного фильтра по фор- муле (66)

дБ.

4. По резонансной кривой с =1 (рисунок 2) определяем значения обобщённых расстроек и , соответствующие ослаблениям , :

=12дБ =2,9,

=2дБ =1,2.

5. Необходимая добротность контуров фильтра, обеспечивающая избирательность по формуле (67)

.

6. Допустимая добротность контуров фильтра, при которой ослабление на краях полосы пропускания составляет по формуле (68)

.

7. Наибольшее значение эквивалентной добротности контуров полосового фильтра, которую можно реализовать с учётом шунтирующего действия входной и выходной проводимостей транзисторов УПЧ и смесителя по формуле (69)

,

где – коэффициент шунтирования контура транзистором, по таблице 8 для БТ выбираем =0,6 ,

– конструктивная добротность контура, по таблице 8 выбираем =150.

8. Проводим проверку выполнения условий 1) и 2) (70), (71)

1) =51,7< =71,3 ,

2) =51,7< =90.

Условия 1) и 2) выполняются. Тогда выбираем эквивалентную добротность контуров фильтра, соблюдая условия 3) (72)

3) , .

Принимаем =60.

9. Для принятых значений =3, =1, =60 определяем фактические значения:

   1. обобщённых расстроек по формулам (73), (74)

,

_;

2. ослабленной , по кривой с =1 (рисунок 2) для расстроек по п.а)

=3,4 =15 дБ,

=1,0 =1,2 дБ;

3. избирательности по соседнему каналу по формуле (75)

= · =15·3=45 дБ;

4. ослабления на краях сквозной полосы пропускания по формуле (76)

= · =1,2·3=3,6 дБ;

В результате расчёта получили, что тракт ПЧ должен содержать число двухконтурных полосовых фильтров =3 с фактором связи =1 и эквивалентной добротностью контуров =60.

При этом он обеспечивает:

• избирательность по соседнему каналу =45 дБ, что больше требуемой по ТЗ (36 дБ);

• ослабление на краях сквозной полосы пропускания 3,6 дБ, что меньше принятого значения для тракта ПЧ в п. 3.5 (6 дБ).