Тербеліс пен толқындар теориясының әдістемелік сұрақтары
Әртүрлі табиғатты тербеліс пен толқындарды оқыту әдістемесі. Толқындардың дисперсиясы, квазибөлшектер. Фотон – электромагнитті әсерлесудің тасымалдаушысы.
Электрмагниттiк және механикалық құбылыстардың ұқсастығын пайдалану - әдiстеменiң тиiмдi нәтижелерiнiң бiрi. Тербелмелi контурдағы токтың энергиясымен бөлшектiң кинетикалық энергиясын, конденсатордың энергиясымен сығылған пружинаның энергиясын теңестiремiз:
.
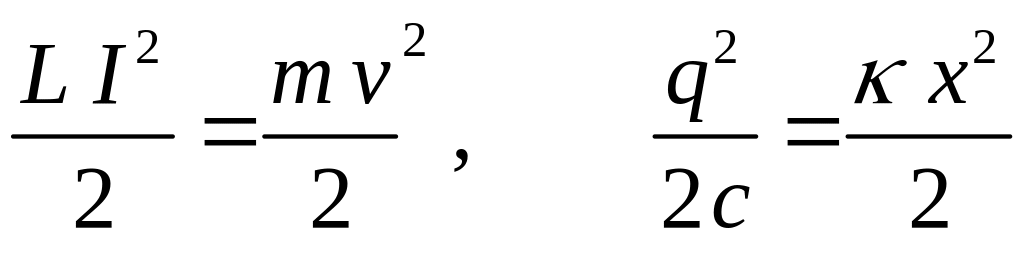(1)
Бұл қатынастардан индуктивтiлiк пен массаның, заряд пен координаттың, сиымдылыққа керi шамамен пружинаның қатаңдылығының ұқсастығы шығады:
.
(2)
Пружинаның тербелiсi мен контурдағы заряд тербелiсiнiң теңдеулерi де ұқсас болады:
.
(3)
(3) - теңдеуден зарядтың тербелiсiнiң, оған сәйкес электр өрiсiнiң кернеулiгiнiң тербелiсiнiң формуласы шығады:
.
(4)
Бұл формуланы электрмагниттiк толқын үшiн жалпылаймыз.
Толқындық
процесте белгiлi қашықтықтан (
- толқын ұзындығы) кейiн физикалық
шамалардың мәнi қайталанады. Егер бiр
нүктеде бақылау жүргiзсек, толқын
(с
- тoлқын
жылдамдығы) уақыттан кейiн қайталанады.
Демек,
=const
шартқа сай уақыт моменттерiнде
толқындық шаманың қасиеттерi бiрдей
болады. Егер
орнына
r жазсақ,
кез келген
r қашықтықпен
кезкелген
t уақытты
байланыстыратын шарт аламыз. (4) - формулада
tt-r/c
алмастыру
жүргiзсек тербелiстiң таралуы- толқындық
процестiң теңдеуiн аламыз:
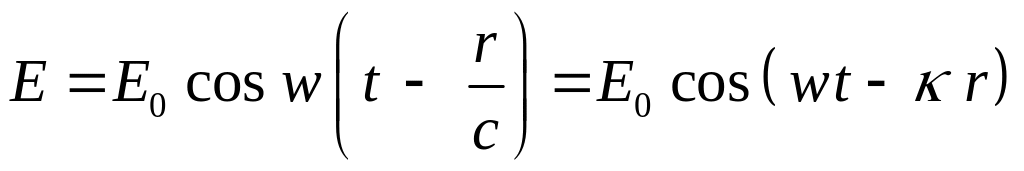(5)
,
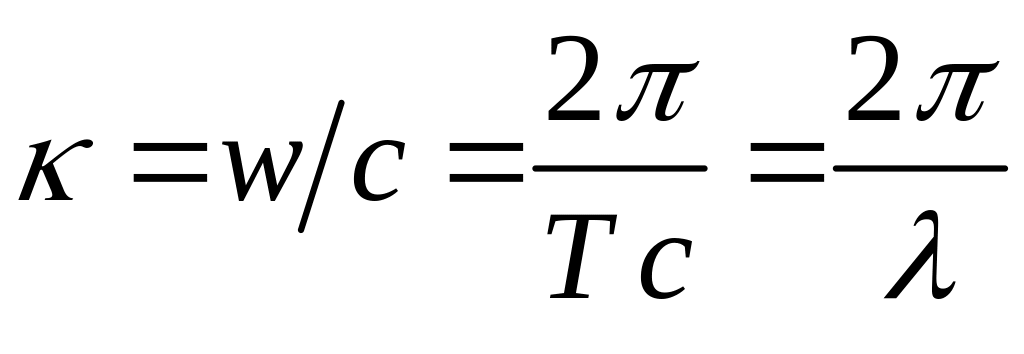мұндағы
к толқындық
сан деп
аталады, Т
- тербелiс
периоды. Толқындық сан - толқындық
вектордың
сан мәнi,
к r
шамасын
скалярлық көбейтiндiнiң
нәтижесi
деп түсiну
керек. Жалпы жағдайда (векторлық түрде)
(6)
.
векторы
толқынның таралу бағытын көрсетедi,
оның құраушылары
x,
y,
z
бағыттарда
толқынның таралуын сипаттайды.
Электрмагниттiк толқын материялық ортада таралғанда дисперсия құбылысы болады. Дисперсия, әдетте, тек жарық толқындарына қатысты айтылады және ол жарықтың сыну көрсеткiшiнiң (n) толқын ұзындығына ( ) байланысын бiлдiредi. Қазiргi физикада толқын ұзындығы кезкелген электрмагниттiк толқын дисперсиясы қарастырылады және дисперсия деп w = w (к) байланысын айтады.
Бұл жағдай оқулықтарда түсiндiрiлмеген, арнайы талқылауды қажет етедi. Кәдiмгi дисперсия үшiн тәжрибелiк формула белгiлi:
,
(7)
мұндағы А, В - тұрақты шамалар. Жиiлiктiң толқындық санға байланысын бейсызық түрде жазайық:
(8)
мұнда
тербелмелi
процестердiң
аргументi
тек тақ дәрежелi
айнымалылар болу керек екендiгi
ескерiлдi.
Егер
екендiгiн
ескерсек (7), (8) формулалардағы
айнымалылардың сәйкес екендiгiн
байқаймыз. Сыну көрсеткiшi
, ал диэлектрик өтiмдiлiк
жиiлiкке
байланысты функция
,
демек
және
байланыстарының физикалық
мәнi
бiр.
Дисперсиялық қатынастардың бейсызық формасы арқылы толқындардың таралуының жаңа заңдылықтары табылды. Мысалы, (8) - формула арқылы судың бетiнде таралатын амплитудасы үлкен, оқшауланған толқынның - солитонның формуласы табылды. Теориялық және тәжрибелiк түрде көптеген бейсызық ортада (сұйық, плазма, қатты дене т.б.) пайда болатын солитондар табылады. Солитонның мысалдары: алып құйындар (циклондар, антициклондар), нерв талшықтарымен өтетiн импульстер - аксондар, өте аз уақыт өмiр сүретiн ядролық резонанстық бөлшектер т.с.с.
Солитон түсiнiгi қазiргi физикада кеңiнен қолданылатын квазибөлшек түсiнiгiмен тығыз байланысты, оның бейсызық ортадағы арнаулы түрi болып табылады. Квазибөлшек - материялық ортадағы элементар қозулар, ұйтқулар , бөлшек тәрiздес шоғырланған толқындар. Басқаша айтқанда, квазибөлшектiң пайда болуы табиғаты әртүрлi (механикалық, электрмагниттiк, т.с.с.) әсердiң, импульстiң ортада жоғалмай таралуы. Анықтамасы бойынша квазибөлшек ылғи да қозғалыста болады. Квазибөлшектердiң мысалдары: сұйықта - турбон, плазмада-плазмон, қатты денеде-фонон, магниттiк ортада-магнон, шала өткiзгiште-экситон, асқын аққыш ортада - ротон т.с.с.
Квазибөлшектiң
физикалық сипаттамаларын оны фотонға
ұқсастырып
анықтаймыз. Фотонның энергиясы
,
импульсi
,
қозғалыс массасы
белгiлi:
.
(9)
Квазибөлшек
үшiн
(8) - формула тәрiздес
дисперсиялық қатынастар, яғни
байланысы, ескерiледi:
.
(10)
Бөлшек
үшiн
импульстiң
сақталу заңы орындалады, ал квазибөлшектiң
импульсi
(квазиимпульс
)
үшiн
сақталу заңы жоқ, өйткенi
соқтығысу нәтижесiнде
толқындар бөлiнуi
мүмкiн,
ал шын бөлшектер (электрондар) бөлiнбейдi.
Квазибөлшек ұғымын ғылымға алғаш
Л.Ландау енгiздi,
сөйтiп
асқын аққыштық, асқын өткiзгiштiк
сияқты күрделi
құбылыстарды түсiндiрдi.
(10) - формулалар ендi фотонның өзiнiң табиғатын тереңiрек түсiнуге мүмкiндiк бердi. Оқулықтарда жазылғандай фотон әрi бөлшек, әрi толқын (электрмагниттiк өрiстiң кванты) деп түсiнудiң көптеген қиындықтары бар. Фотон үшiн “бөлшек” деген сөздiң кәдiмгi мағынасы жоқ: оның тыныштық массасы жоқ, заряды жоқ, оның зат iшiндегi өмiр сүру уақыты белгiсiз, т.с.с.
Егер фотонды физикалық вакуумде тұрақты с жылдамдықпен қозғалатын квазибөлшек деп қабылдасақ, айтылған әдiстемелiк қиындықтың бәрi шешiледi. Фотон үшiн физикалық вакуум дегенiмiз электрон-позитрондық құрылымы бар әлемдiк кеңiстiк. Бұл тұжырым кванттық электрдинамика ғылымының негiзi. Сонымен, фотон - ерекше ортаның квазибөлшегi. Осыдан кейiн физика оқулықтарындағы белгiлi “энергияның және импульстiң сақталу заңдарын пайдаланып фотонның электрон-позитрон жұбына айналуын неге сипаттауға болмайды” деген сұраққа жауап бiрден берiледi, квазиимпульс сақталмайды.
Лекция 13