5. Предел числовой последовательности.

Числовой последовательностью называется бесконечное множество чисел

    (1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого   задается как функция целочисленного аргумента,   т.е.   .

Число А называется пределом последовательности (1), если для любого    существует число   , такое, что при   выполняется неравенство   . Если число А есть предел последовательности (1), то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

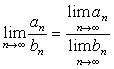
 если   .

6. Предел функции в точке. Предел функции на бесконечности.

Число   называется пределом функции   на бесконечности или при  , если для любого   существует число   такое, что для всех   из того, что  , выполняется неравенство  .

Определение предела функции в точке по Коши.

Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа  существует такое положительное число , что при всех х ≠ а, таких, что |x – a | < , выполняется неравенство | f(x) – a | <  .

Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {x_n}, стремящейся к а( имеющей пределом число а), причем ни при каком значении n х_n ≠ а, последовательность {y_n = f(x_n)} сходится к b.

Данные определения предполагают, что функция у = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а.

7. Основные теоремы о пределах.

 

Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

   .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

   .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с,    докажем, что     .

Возьмем  произвольное >0. В качестве  можно взять любое

положительное число. Тогда при 

.

Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

  и   .

По теореме о связи предела и бесконечно малой функции:

f(x)-A=  - б.м. при  ,

f(x)-B=  - б.м. при  .

Вычитая эти равенства, получим:

 B-A= - .

Переходя к пределам в обеих частях равенства при  , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при  , то и алгебраическая сумма имеет предел при  , причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть  ,   ,    .

Тогда, по теореме о связи предела и б.м. функции:

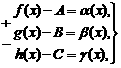 где   - б.м. при .

Сложим алгебраически эти  равенства:

f(x)+g(x)-h(x)-(А+В-С)= ,

где  б.м. при   .

По теореме о связи предела и б.м. функции:

А+В-С= .

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при  , то и произведение имеет предел при , причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при  ,

причем  , то и их частное имеет предел при  , причем предел частного равен частному пределов.

,   .
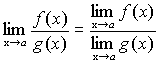