Симметрия элементарной ячейки.

Симметрия элементарной ячейки определяется следующими факторами:

1. метрикой элементарной ячейки (осевые отрезки и углы)

2. расположением центров тяжести точек (частиц) в элементарной ячейке.

3. Собственной симметрией точек.

4. Ориентировкой точек по отношению к осям элементарных ячеек.

3. Кристаллохимия.

Кристаллография – наука о кристаллах. Кристаллография изучает законы образования и структуру и физические свойства кристаллов, влияние на них внешних факторов. Кристаллография является разделом физики твердого тела. Основные экспериментальные методы кристаллографии: нейтронография, рентгенография, электронография.

Кристаллохимия – наука, исследующая зависимость физико-химических свойств кристаллических веществ и кристаллических материалов от их кристаллической структуры и химического состава, рассматриваемых в совокупности. Кристаллохимия изучает законы расположения атомов (ионов, молекул) в кристаллах соединений и сплавов и влияние этих законов на свойства последних. В задачи этой науки входит объяснение причин образования химическими соединениями данных конкретных типов структуры. Кристаллохимия – в определенном смысле синтез стереохимии и кристаллографии.

Кристаллические аспекты строения кристалла. Основные типы пространственных решеток. Плотные упаковки.

Если условно рассматривать атомы в кристалле как касающиеся друг друга шары, то возникает вопрос, каким образом можно их наиболее плотно уложить, т.е. создать структуру с наиболее плотной упаковкой (с минимально незанятым атомами объемом). Анализ приводит к выводу о том, что возможны только две исходные плотнейшие упаковки: кубическая и гексагональная.

Существует только одно решение задачи плотнейшей упаковки шаров одинакового диаметра в одной плоскости; вокруг центрального шара должно быть расположено 6 шаров в вершинах правильного шестиугольника как показано на рис 1.62а.

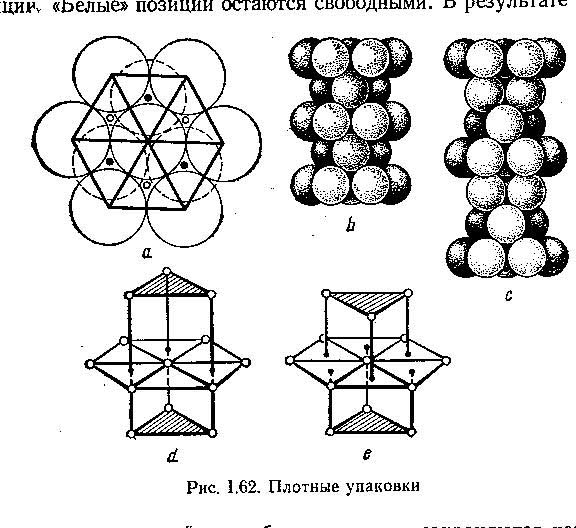
Если следующий ряд укладывать на первый так, чтобы центры тяжести шаров приходились друг над другом, плотная упаковка не получится: надо укладывать шары второго рода в промежутки между шарами первого ряда (рис.1.62 - пунктир). Центры тяжести шаров второго ряда показаны черными кружками. До сих пор упаковка по кубическому и гексагональному закону совпадает.

Если теперь шары третьего ряда уложить так, что их центры тяжести придутся над центрами тяжести шаров первого ряда (рис. 1.62б) получится плотнейшая гексагональная упаковка. Если шары третьего ряда уложить так, что их центры придутся над позициями отмеченными белыми кружками, на рис.1.62а, а шары четвертого ряда над шарами первого ряда, то получим плотнейшую кубическую упаковку (рис. 1.62с). На рис. 1.62 d,e показано расположение атомов первой координационной сферы в плотнейшей гексагональной и плотнейшей кубической упаковке. В гексагональной упаковке треугольники нижнего и верхнего оснований повернуты в одну и ту же сторону, а в кубической в разные.

В ГПУ шары первого и третьего ряда кладутся друг над другом, занимая “черные” позиции. “Белые” позиции остаются свободными. В результате по всей вертикали, проходящей через “белые” позиции сохраняются незанятые места, похожие на шахты. По этим шахтам может происходить диффузия примесей.

Напротив, в кубической упаковке шары второго и третьего, пятого и шестого и т.д. рядов поочередно занимают то “белые”, то ”черные“ позиции, уничтожая сквозные шахты.

Тогда как ГПУ отвечает элементарной ячейке, плотнейшая кубическая упаковка не сразу ассоциируется с кубической гранецентрированной элементарной ячейкой. Эта упаковка видна на рис.1.63 а, где представлены две смежные элементарные ячейки.

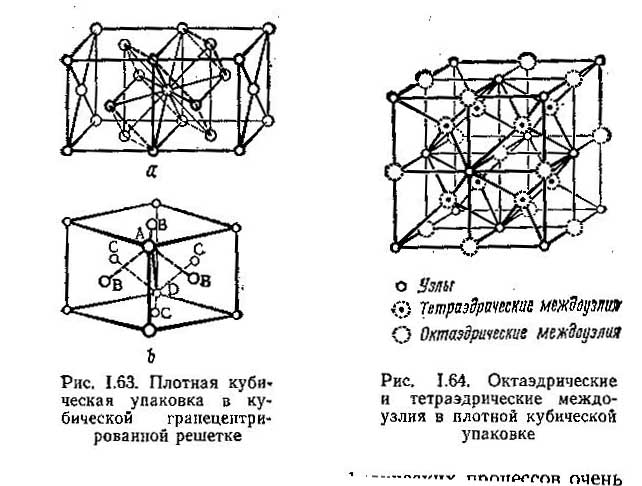
Центральный атом шестиугольника лежит на середине смежной грани двух ячеек и имеет 12 соседей.

Чтобы показать для этой структуры расположение атомов в вершинах правильного шестиугольника, он выделен пунктиром, так и два треугольника, отвечающие рис. 1.62е.

Междоузлия (промежуточные позиции между узлами в кристаллической ячейке) плотных упаковок бывают двух типов: октаэдрические и тетраэдрические. На рис. 1.64 показаны междоузлия элементарной ячейки плотной кубической упаковки. Октаэдрические междоузлия располагаются в центрах 12 ребер и в центре элементарной ячейки: всего их (12/4) + (1/1) (т.е. столько же сколько позиций атомов). Тетраэдрические междоузлия располагаются в центре 8 октантов (кубов с ребром а/2, т.е. объемом равным 1/8 объема ячейки), всего их имеется в элементарной ячейке 8/1=0, т.е. вдвое больше, чем позиций атомов. В кубической ячейке диаметр октаэдрической пустоты 0,41D, тетраэдрической – 0,22D, где D – размер атома.

Роль междоузлий в протекании физических процессов очень велика. Атомы могут смещаться в междоузлия, диффундировать, передвигаться по ним. Позиции в междоузлиях могут целиком или частично быть заняты атомами других элементов, что приводит к изменению свойств и к образованию других структур.

В теории структур часто пользуются методом укладки тетраэдров, а не шаров для интерпретации процессов образования тех же (и других) упаковок (рис. 1.65)

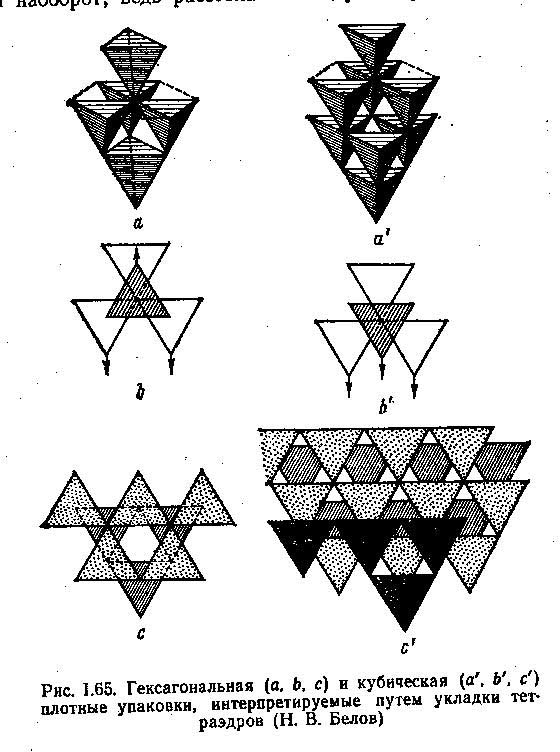
Можно мысленно объединить линиями центры шести шаров первого ряда, образовав верхние грани трех тетраэдров. Затем проведя ребра этих тетраэдров к трем шарам, лежащим в нижнем ряду, получим средние три тетраэдра (рис. 1.65 а) на котором показано расположение тетраэдров двух рядов, примыкающих снизу и сверху к тетаэдрам среднего ряда.

В гексагональной упаковке, тетраэдры двух соседних рядов повернуты вершинами в разные стороны, как показано стрелками на рис. 1.65b. так как тетраэдры первого и третьего рядов лежат точно друг под другом, то образуются сквозные люки, хорошо видимые на рис. 1.65с.

На рис.1.65 а’ показана “четырехэтажная” постройка кубической упаковки из тетраэдров, в которой тетраэдры соседних рядов повернуты вершинами в одну и ту же сторону (рис.1.65 b’), так что шахты перекрываются (рис. 1.65с’).

Структуры чередования. Понятие фазы.

Некоторые металлы образуют структуру только с плотной кубической упаковкой (Cu, Ag, Au), другие только с плотной гексагональной (Mg, Zn, Cd), но некоторые образуют обе структуры (Ca, Ni, Co). Для последних характерен фазовый переход I рода (ниже некоторой температуры одна, выше – вторая модификация). Именно в этих случаях особенно реально «застревание» в решетке одного типа слоев (очагов) решетки второго типа.

Фаза – химически и термодинамически однородные части гетерогенной системы, отделяющиеся друг от друга видимыми границами раздела.

Основные типы кристалических структур.

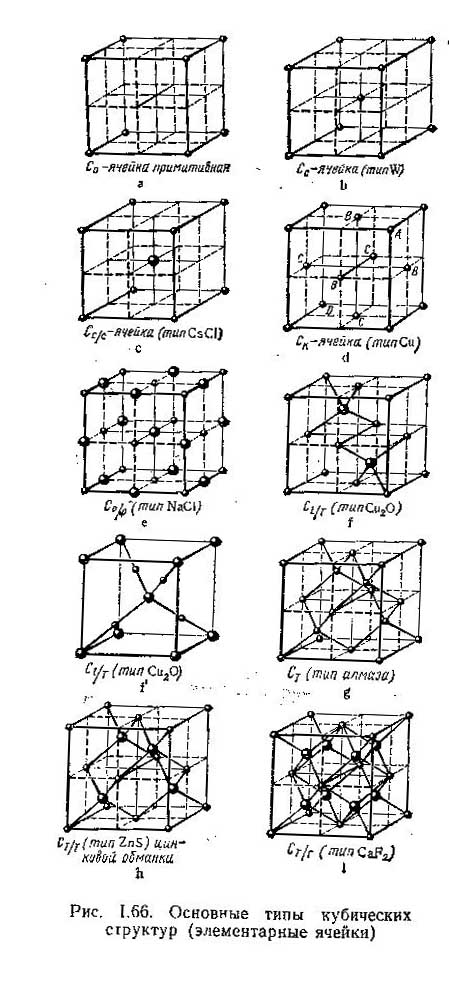
На рис. 1.66 показаны следующие типы структур кубических видов симметрии

Рис.	Тип решетки	Вид симметрии	КЧ	Представители
A	P-прим.	Oh-m3m	6/6	-Po
B	I – ОЦ, двукратно прим.	Oh-m3m	8/8	W, ЩМ, V, Nb, Ta
C	ОЦ двукратно прим типа CsCl	Oh-m3m	8/8	CsBr, CsI, RbCl
D	Кубическая ГЦ, четырехкратно прим., типа Cu	Oh-m3m	12/12	Cu
E	Тип NaCl, восьмикратно прим.	Oh-m3m	6/6	Полупроводники PbS, PbSe, PbTe
F	Тип Cu2O шестикратно прим.	Oh-m3m	4/2	Cu2O
F’	ОЦ I – ячейка	Oh-m3m	4/2	Cu2O
G	Восьмикратно прим. Решетка типа алмаза	Oh-m3m	4/4	Полупроводники Si, Ge, серое олово
H	Восьмикратно прим. ячейка типа сфалерита типа цинковой обманки ZnS	Td-43m	4/4	AlP, AlAs, AlSb
I	Двенадцатикратн. Прим. ячейка типа флюарита CaF2	Oh-m3m	8/4	Полупроводники Mg2Si, Mg2Ge

Рассматривая структурный тип Cu на рис. 1.64, можно видеть, что в нем две группы междоузлий: октаэдрические и тетраэдрические.

Если ввести в кубическую гранецентрированную решетку вторую такую же, так чтобы точка (1/2 ½ 1/2) второй совпадала с точкой (000) первой, то возникает решетка типа NaCl (рис.1.66 е)с восьмикратно примитивной ячейкой кч 6/6, в которой и будут заняты все четыре октаэдрические междоузлия.

В кубической гранецентрированной ячейке типа Cu можно заменять атомами и различные тетраэдрические междоузлия в центрах октантов. Так можно заменять атомами кислорода два октанта по диагонали. При этом возникает шестикратно примитивная решетка куприта Cu₂O (графа F и рис. 1.66 f). В литературе обычно дается другая структура куприта (рис 1.66 f’): в объемно центрированную I – ячейку из атомов O вставлены четыре атома Cu в центах четырех октантов посередине расстояний O-O в тетраэдрическом координационном многограннике.

Если в решетку типа меди ввести вторую такую же, но так, чтобы (000) атом второй занял (1/4 ¼ 1/4) позицию первой, получим восьмикратно примитивную решетку алмаза, кч 4/4 (рис. 1.66 g и в табл. g).

Если же вторая решетка будет состоять из атомов иного элемента, чем первая получается восьмикратно примитивная элементарная ячейка типа сфалерита, цинковой обманки ZnS рис. 1.66 h и в табл. H)

Если в решетку типа меди ввести две такие же, но образованные атомами иного элемента и притом так, что нулевой атом второй займет (1/4 1/4 1/4) позицию первой, а нулевой атом третьей (3/4 ¼ 1/4) позицию первой, то получится решетка типа флюорита CaF₂.

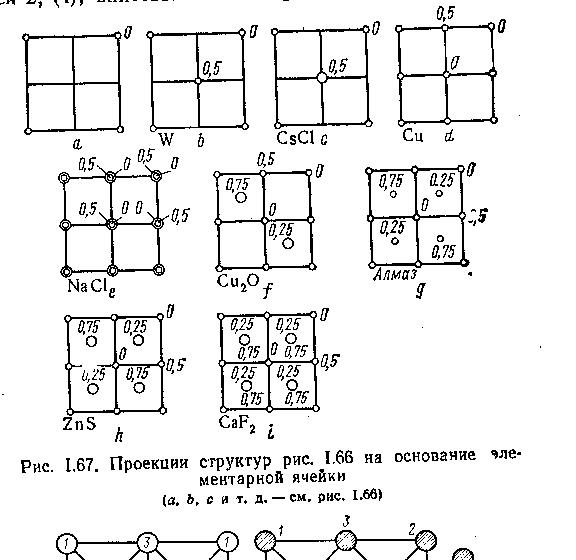
На рис. 1.67 показаны проекции этих структур. Цифры около кружков, представляющих собой проекции центров тяжести атомов на площадь основания ячейки, указывают высоту данной позиции в ячейках в долях a. Ноль обозначает, что позиция лежит в основании ячейки.

Решетка алмаза и цинковой обманки весьма близки, в то же время структура алмаза относится к виду симметрии O_h, тогда как структура цинковой обманки – к гораздо более низкосимметричному виду T_d.