Построение зон Бриллюэна в простой кубической решетке с параметром а

Обратная решетка также будет простой кубической, с параметром . Ячейка Вигнера-Зейтца в –пространстве, т.е. первая зона Бриллюэна, представляет собой в этом случае куб с объемом 8³/a³. Куб, построенный на трех взаимно перпендикулярных векторах длиной содержит все неэквивалентные точки, поскольку они не могут быть получены одна из другой, с помощью какого-либо вектора . Все точки лежащие вне этого куба можно получить из точек, расположенных внутри куба. Для построения превой зоны Бриллюэна, необходимо сместить все точки на вектор . При этом центр куба совмещается с началом отсчета . все неэквивалентные значения компонентов вектора лежат в интервалах

Несколько зон Бриллюэна построены на рисунке.

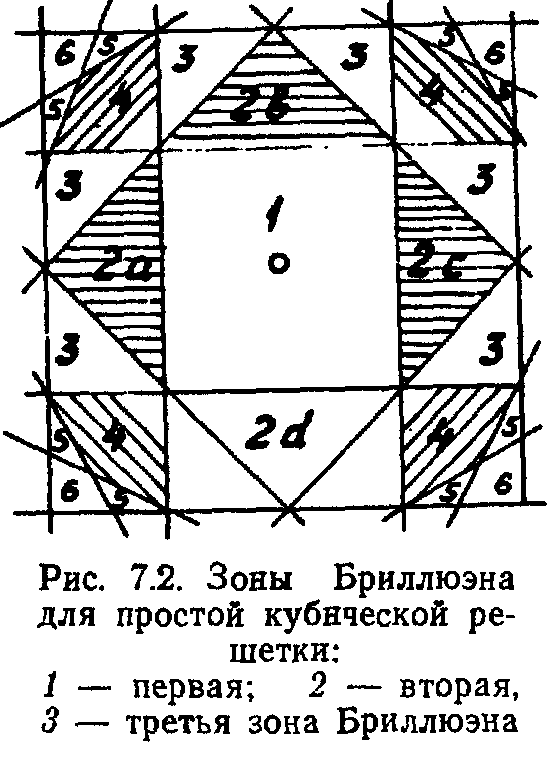
Эквивалентность физических состояний, принадлежащих различным зонам Бриллюэна, позволяет при движении электрона в -пространстве рассматривать его траекторию только в пределах первой зоны Бриллюэна.

Реальный кристалл является ограниченным. Это приводит к тому, что волновой вектор электрона в кристалле может принимать только дискретный ряд значений. Для того, чтобы подсчитать число допустимых значений в зоне Бриллюэна, необходимо учесть граничные условия. Если кристалл имеет форму паралеллепипедас размерами по осям x, y, z соответственно L_x, L_y, L_z, решетка простая кубическая с параметром а, тогда

-число атомов, располагающихся на ребрах соответственно. Необходимо удовлетворение функции условию Борна-Кармана

т.е. волновая функция электрона в кристалле имеет вид функции Блоха, приведенное условие может быть приведено к виду

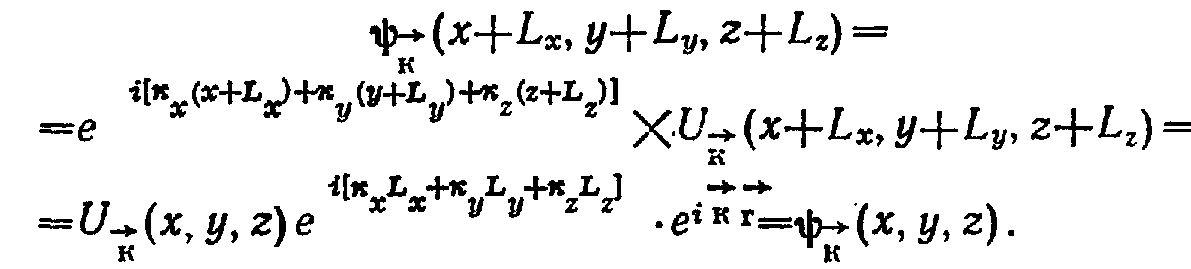
Здесь учтено, что условие выполняется вследствие периодичности функции. содержит целое число периодов решетки. Для выполнения вышеуказанного условия необходимо принять

Или

Равенство выполняется если

Отсюда получаем разрешенные значения компонентов волнового вектора

В силу связи между и энергией , последняя оказывается квантованой.

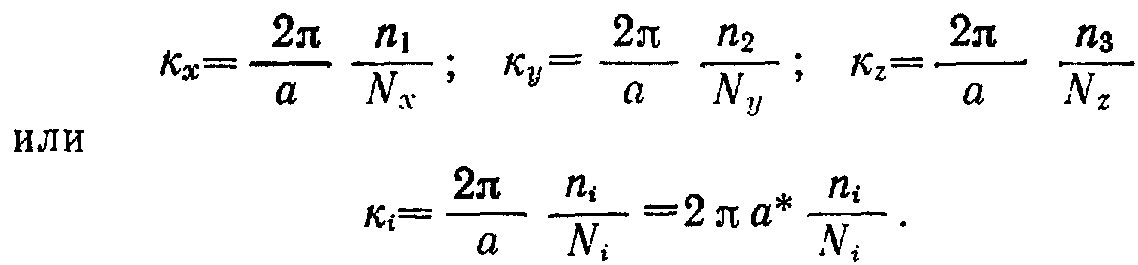
т.к. состояния с волновыми векторами эквивалентны, можно рассматривать не бесконечный ряд значений n_i, а ограничить его условием

нижнее значение n_i = 0.

Число разрешенных значений компонентов вектора заключенных в интервалах

составляет для . Всего в зоне Бриллюэна имеется

разрешенных состяний

N равно числу элементарных ячеек в кристалле.

Для полного описания всей совокупности состояния электрона в кристалле, достаточно рассматривать только область значений ограниченную первой зоной Бриллюэна. Волновой вектор может изменяться по всему –пространству, поскольку для любых двух значений , отличающихся на вектор все волновые функции и уровни энергии одинаковы.

При заданном n собственные функции и собственные значения уравнения Шредингера были периодическими функциями вектора в обратной решетке.

Совокупность всех энергетических уровней электрона описывается функцией при фиксированном значении n, называют энергетической зоной

Т.к. каждая функция периодична и квазинепрерывна, у нее существует верхний и нижний пределы. Все уровни энергий данной энергетической зоны заключены в интервале между двумя пределами.

При ширине зоны  1 эВ среднее расстояние между энергетическими уровнями составляет 10^-22 эВ т.е. много меньше k_BT. Именно этот факт в ряде случаев не учитывает дискретность в пределах зоны.

Поскольку каждому значению соответствует разрешенный уровень энергии и на каждом уровне в силу принципа Паули может размещаться два электорна с противоположно направленными спинами, число электронов не может быть больше чем 2N.