Одноэлекторонное приближение

Многоэлектронная задача может быть сведена к одноэлектронной методом Хартри – Фока, где потенциальная энергия взаимодействия электронов

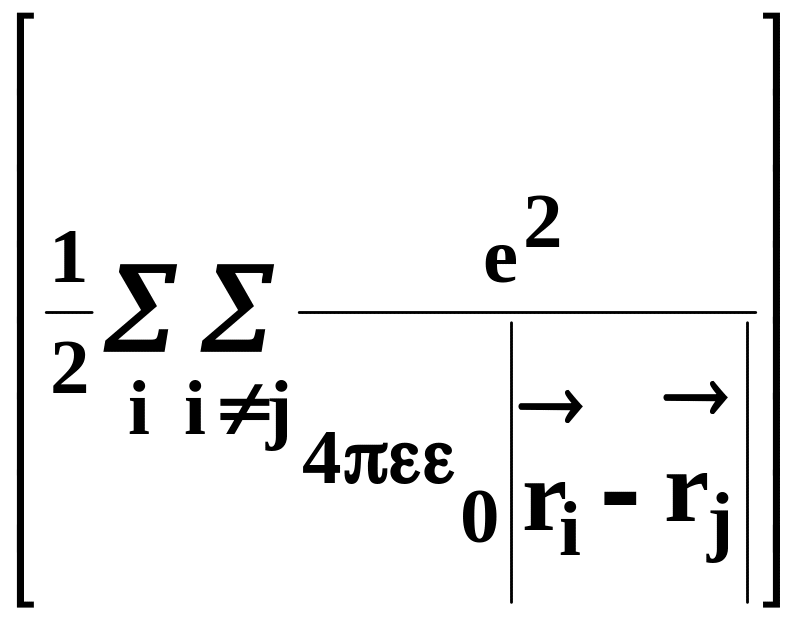
заменяется потенциальной энергией вида , представляющей собой энергию взаимодействия i –го электрона с некоторым эффективным полем, в котором каждый электрон движется независимо. Это эффективное поле характеризует действие всех остальных электронов на i – й электрон, т.к. он оказывает воздействие на движение всех остальных электронов.

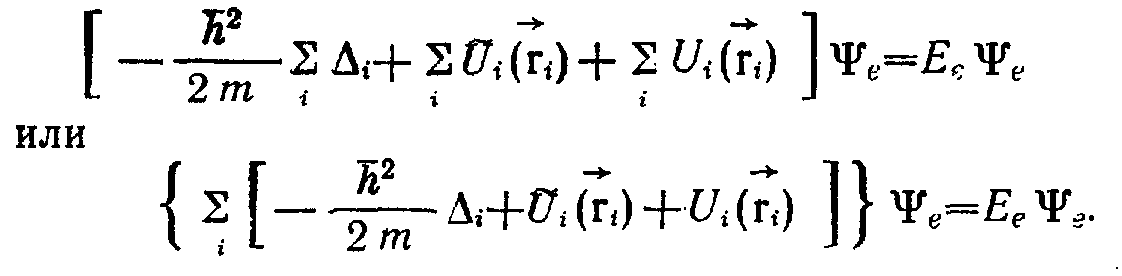
Под знаком суммы стоит гамильтониан i – го электрона

Уравнение Шредингера принимает вид

Т.к. гамильтониан не содержит энергии взаимодействия электронов и представляет собой сумму гамильтонианов отдельных электронов, решением уравнения является произведение одноэлектронных функций

Каждая функция удовлетворяет одноэлектронному уравнению Шредингера.

В котором взаимодействие i – го электрона с остальными описывается потенциалом

Таким образом введение эффективного поля позволяет свести многоэлектронное уравнение к системе одноэлектронных. При этом энергия системы

Волновая функция

является решением уравнения Шредингера, но не удовлетворяет принципу Паули, по причине неудовлетворения функции

Антисимметричную функцию записывают в виде определителя Слэттера

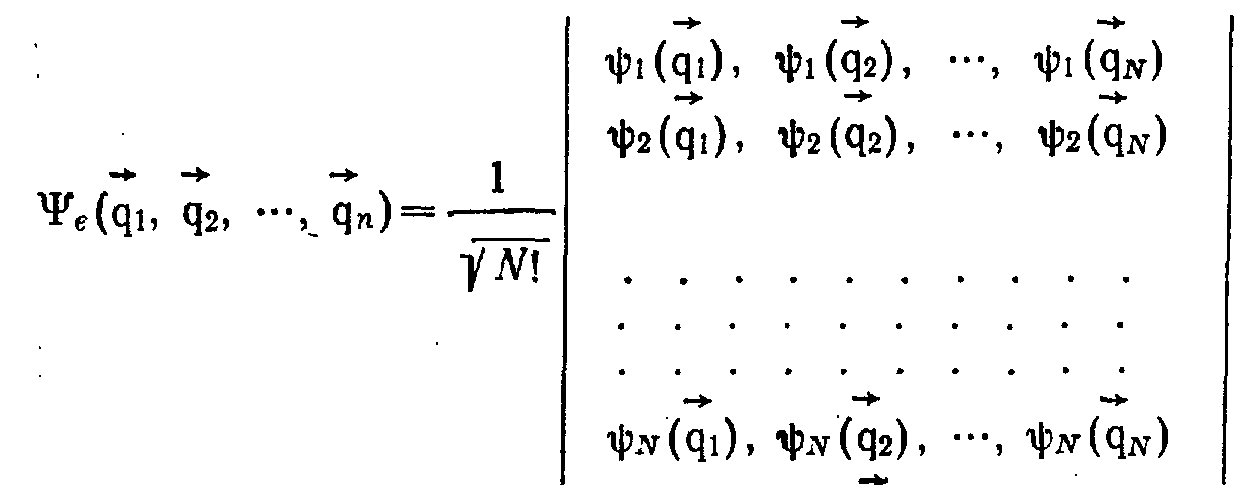
Если обозначить потенциальную энергию через

уравнение Шредингера имеет вид

является периодической функцией и ее период совпадает с периодом кристаллической решетки.

Функции Блоха

Ф. Блохом доказано, что волновые функции являются решением уравнения Шредингера с периодическим потенциалом, имеющим период решетки, представляют собой плоские волны, модулированные некоторой функцией с периодичностью решетки.

- некоторая периодическая функция с периодом решетки, зависящая от длины волнового вектора k.

Условия периодичности потенциальной энергии электрона в кристалле

При смещении кристалла на вектор

, они совмещаются сами с собой. Из условия трансляционной симметрии следует, что волновая функция электрона отличается от волновой функции некоторым постоянным множителем

Из условия нормировки следует, что

Этому можно удовлетворить, если предположить, что

К - волновой вектор, характеризующий квантовое состояние электрона в кристале. Показатель степени экспоненты – безразмерная величина. Если - размерность длины, то к – размерность обратная длине, т.е. см^-1. модуль вектора к является волновым числом. Физический смысл – число длин волн, укладывающихся на отрезке 2.

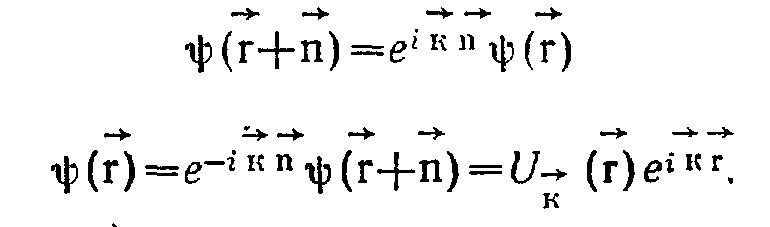
Здесь через

обозначена функция

Являющаяся периодической с периодом решетки

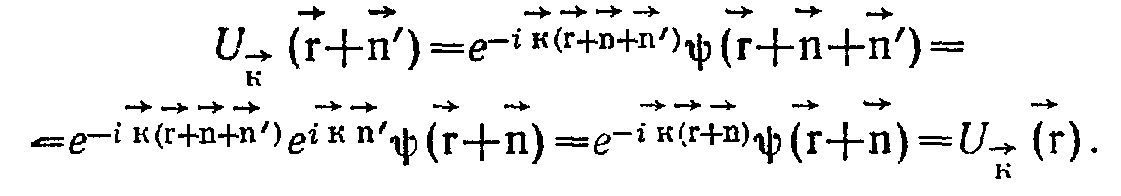
Волновая функция электрона в кристалле представляет собой бегущую волну , модулированную периодической функцией , имеющей период решетки и зависящей от волнового вектора к.

Функция называется функцией Блоха.

Свойства волнового вектора электрона в кристалле. Зоны Бриллюэна.

Волновой вектор играет в задаче о движении электрона в периодическом поле кристалла такую же роль, какую играет волновой вектор в задаче о движении электрона. Состояние свободно движущегося электрона характеризуется энергией E и импульсом , при этом

Этому электрону соответствует волна де Бройля с длиной

 - скорость электрона, учитывая, что

волновой вектор пропорционален импульсу электрона. Энергия свободного электрона связана с соотношением

Если на электрон не действует никакая сила, то . Это означает, что не изменяется и остается постоянным импульс . По существу это закон сохранения энергии.

На электрон, движущийся в кристалле, действует периодическое поле кристаллической решетки. Энергия этого взаимодействия является периодической функцией координат. Следовательно, энергия и импульс электрона в кристалле изменяются со временем под действием этого поля, т.е. не сохраняются.

Пользуясь понятием волнового ветора , входящего в функцию Блоха, можно ввести характеристику, аналогичную импульсу, но сохраняющуюся во времени

Величина называется квазиимпульсом электрона

Если какая-либо величина сохраняется, то оператор этой величины коммутирует с оператором Гамильтона. Таким образом, квазиимпульсу должен соответствовать некоторый оператор , коммутирующий с гамильтонианом кристаллической решетки.

Следовательно, можно утверждать, что при движении электрона в периодическом поле решетки, собственные функции операторов должны быть одинаковы, а между значениями определенная функциональная связь.

Энергия электрона должна быть функцией квазиимпульса. Оператор не может иметь вид обычного оператора импульса , поскольку он не коммутирует с гамильтонианом решетки

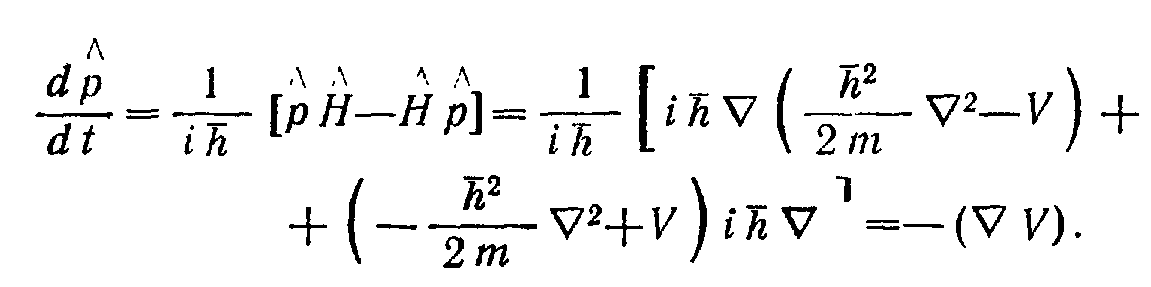
С другой стороны, между гамильтонианом квазиимпульса и оператором импульса должна быть связь.

Если потенциальная энергия решетки постоянна т.е. , то в этом случае квазиимпульс переходит в импульс.

Оператор квазиимпульса

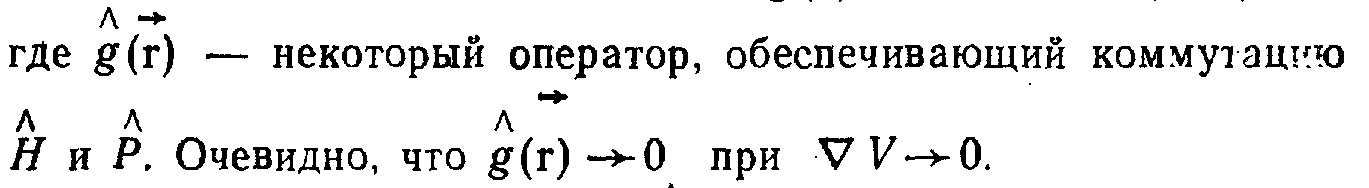
Для определения оператора

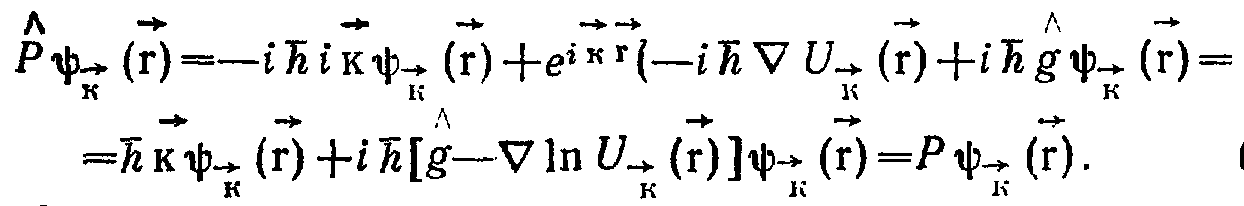
Тогда

Отсюда

Если

,

то в функции Блоха будет стремиться к некоторой константе. При этом и квазиимпульс превращается в импульс.

Волновой вектор электрона в кристалле, в отличие от волнового вектора свободного электрона неоднозначен. Рассмотри трансляционное уравнение, накладываемое на волновую функцию электрона, движущегося в периодическом поле решетки.

Условие не нарушается, если волновой вектор заменить на вектор

-вектор обратоной решетки.

Состояния характеризуемые векторами физически эквивалентны. Энергия электронов, находящихся в этих состояниях, одинакова.

Волновая функция и энергия электрона в кристалле являются периодическими функциями волнового вектора с периодом (или квазиимпульса ).

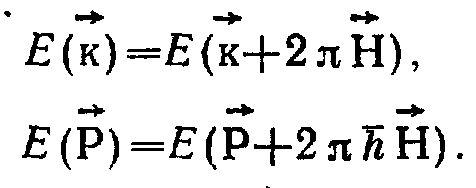
Если в -пространстве (или -пространстве) построить обратную решетку, растянутую в 2 раз, т.е. решетку с векторами , то все -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна. Многогранник минимального объема, построенный вокруг начала координат в -пространстве, содержащий все возможные различные состояния, называется первой или основной зоной Бриллюэна. С помощью обратной решетки, любую точку -пространства можно обратить в первую зону Бриллюэна. Первая зона Бриллюэна представляет собой элементарную ячейку Вигнера – Зейтца для обратной решетки, растянутой в 2 раз. Вторая зона строится аналогичным образом. В обратной решетке, параметры которой растянуты в 2 раз, выбранный при построении первой зоны Бриллюэна за начало отсчета узел, соединяют прямыми линиями с ближайшими эквивалентными узлами, но уже лежащими на поверхности второй координационной сферы. Затем строят плоскости, перпендикулярные этим прямым и проходящим через их середину. В результате получают вторую зону Бриллюэна в виде замкнутого многогранника.