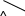Анализ полученных выражений показывает, что выделенные кинематические цепи являются структурными группами.
1.14. Классификация структурных групп по Артоболевскому
№ п/п |
Структурная схема |
Номер звеньев образующих группу |
Класс, порядок, вид |
1 |
1 А |
0-1 |
1 класс |
2 |
2
3
|
2-3
|
II класс 2 порядок 5 вид |
3 |
4 5 |
4-5 |
II класс 2 порядок 1 вид |
2.Кинематический анализ
2. Кинематический анализ рычажного механизма строгального станка.
2.1 Определение крайних (мертвых) положений механизма.
Для шарнирного кривошипно-коромыслового четырехзвенника крайними будут такие положения, когда кривошип и ползун то вытягиваются, то складываются в одну линию (рис 2.1).
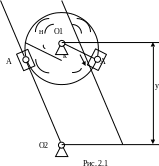
Крайние положения механизма.
Тогда определятся начальный и конечный углы φн = 187.98˚, φк = 352.02˚.
2.2. Определение положений звеньев механизма.
2.2.1. Построение планов положений исследуемого механизма станка.
Выбираем
масштабный коэффициент длин
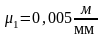и рассчитываем чертежные размеры звеньев
(табл. 2.2).
Т а б л и ц а 2.2.
Чертежные размеры звеньев
О1А, мм |
О1О2,мм |
О2В,мм |
ВС,мм |
У, мм |
Уд, мм |
20 |
144 |
254 |
88 |
110 |
22 |
Строим планы механизма (рис.2.2).
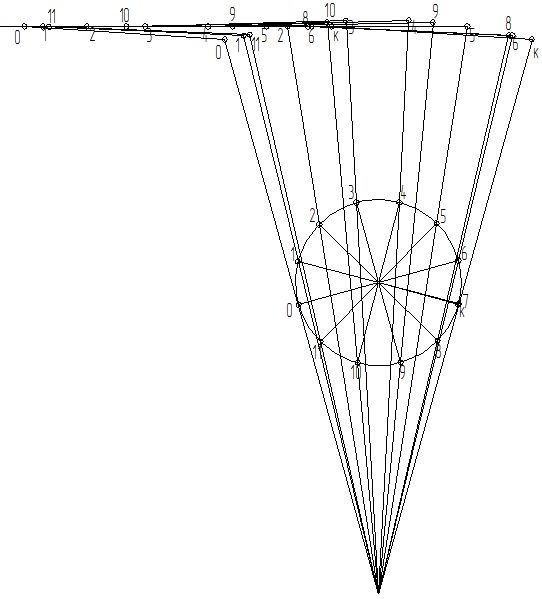
Рис. 2.2. Планы механизма.
2.3 Кинематическое исследование машин и механизмов
аналитическим методом.
2.3.1. Кинематическое исследование механизма аналитическим методом.
Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.
1. Рисуем во втором промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
4. Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: О1-А-О2-О1, О2-F-С-В-О2 (рис2.2)
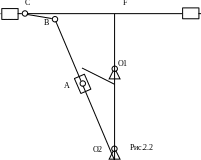
2.3.2. Построение замкнутых векторных контуров.
Для исследования механизма применим метод замкнутых векторных контуров. Механизм разбиваем на два контура : О1-А-О2-О1, О2-F-С-В-О2 (рис2.2).
2.3.3.Определение положений звеньев механизма и центров их тяжести.
Рассмотрим контур О1-А-О2-О1
Записываем уравнение замкнутости первого контура в векторной форме:
L1+L31+Ly1 = 0
Проецируем эти вектора на оси координат и получаем систему уравнений
L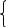
1cos(1)
+ L31cos(3)
+ y1cos(y1)=0
L1sin(1) + L31sin(3) + y1sin(y1)=0
или
L 1cos(1) + L31cos(3) =0 (2.1)
L1sin(1) + L31sin(3) + y1=0
Из этой системы находим неизвестные.
3 = arctg[((y1+L1sin(1)/-L1cos(1)]
Подставив, найденный угол 3 в одно из уравнений найдём L31.
L31= [-L1cos(1)/cos(3)]
Рассмотрим второй контур (рис. 2.2).
Записываем уравнение замкнутости второго контура в векторной форме:
а+в+L4+L3 = 0
Проецируем эти векторы на оси координат и получаем систему уравнений
L 3cos(3) + L4cos(4) + bcos(b)+a cos(a) =0
L3sin(3) + L3sin(4) + bsin(b)+asin(a) =0
или
L 3cos(3) + L4cos(4) - b =0 (2.2)
L3sin(3) + L3sin(4) + a =0
Из этой системы находим неизвестные.
4 = arcsin [(-L3sin(3)-a)/L4]
Подставив, найденный угол 4 в первое уравнение найдём b.
b= L4cos(4)+L3cos(3)
2.3.4 Определяем начало и конец рабочего хода.
Для этого определяем разницу между крайними положениями точки С и отнимаем
2Н/10, это будет длина рабочего хода. Длина вектора b, характеризующего начало
р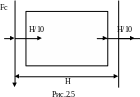
абочего
хода будет bн-H/10,
конец bк
+H/10.
Подставив полученные b в систему уравнений
2.2, и вычислим неизвестные углы 3
и
4.
Найденный угол 3
подставим
в систему уравнений 2.1 и найдём недостающие
данные , т.е. 1,
L31.
Подробный расчет с результатами приведен
в приложении.
Для определения координат центров масс звена 4 запишем замкнутый контур:
О2-В-S4-О2 в проекциях на оси координат.
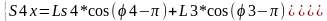
Координаты центра масс звена 3:
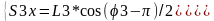
Для определения координат центров масс звена 4 запишем замкнутый контур:
О2-В-S4-О2 в проекциях на оси координат.
Координаты центра масс звена 3:
2.3.5. Находим скорости звеньев.
Для нахождения скоростей звеньев надо взять производную от системы
уравнений 2.1 и в результате получим:
- L1sin(1)+L’31cos(3)-L31sin(3)* ’3=0 2.4
L1cos(1)+L’31sin(3)+L31cos(3)* ’3=0
Вычтем, из каждого угла 3 и получим:
- L1sin(1-3)+L’31=0
L1cos(1-3)-L31 ’3=0
Из этой системы уравнений находим скорость камня вдоль кулисы L’31 , и
угловую скорость кулисы т.к. считаем, что угловая скорость первого звена
равна 1.
L’31=L1sin(1-3)
’3=L1cos(1-3)/L31
Находим скорости звеньев второго контура. Для нахождения скоростей звеньев
второго контура надо взять производную от системы уравнений 2.2 и в
результате получим:
- L4sin(4)* ’4-L3 sin(3)* ’3-b’=0 2.5
L4cos(4)* ’4+L3cos(3)* ’3=0
Если мы из каждого угла вычтем угол 4, то получим:
- L3 sin(3-4)* ’3-b’=0
L4’4+L3cos(3-4)* ’3=0
Из этой системы уравнений находим скорость ползуна b’ и угловую скорость
шатуна ’4.
b’=-L3 sin(3-4)* ’3
’4= (L3cos(3-4)* ’3)/ L4
Скорости центров масс, так же находим дифференцированием соответствующих
систем .
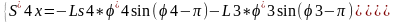
Скорость S5x совпадает со скоростью т. b.
Находим ускорения звеньев первого контура.
Для нахождения ускорения звеньев первого контура надо взять производную
от системы уравнений 2.4 и в результате получим:
-
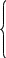L1cos(1)+L’’31cos(3)-L’31sin(3)*
’3-
L’31sin(3)*
’3-
L31cos(3)*
(’3)2-
-L31sin(3)* ’’3=0 2.4
-L1sin(1)+L’’31sin(3)+L’31cos(3)* ’3+ L’31cos(3)* ’3- L31sin(3)*(’3)2+
+L31cos(3)* ’’3=0
Если мы из каждого угла вычтем угол 3 ,то получим:
- L1cos(1-3)+L’’31cos(3-3)-L’31sin(3-3)* ’3- L’31sin(3-3)* ’3-
-L31cos(3-3)* (’3)2-L31sin(3-3)* ’’3=0
-L1sin(1-3)+L’’31sin(3-3)+L’31cos(3-3)* ’3+ L’31cos(3-3)* ’3-
-L31sin(3-3)*(’3)2+L31cos(3-3)* ’’3=0
-
L1cos(1-3)+L’’31-L31*
(’3)2=0
-L1sin(1-3)+L’31 ’3+ L’31 ’3-L31 ’’3=0
Из этой системы уравнений находим ускорение камня вдоль кулисы L’’31 и
угловое ускорение кулисы ’’3 т.к. считаем ,что первое звено движется
равномерно с постоянным по модулю угловым ускорением.
L’’31=L1cos(1-3)+ L31* (’3)2
’’3=(L1sin(1-3)-2L’31 ’3)/L31
Находим ускорения звеньев второго контура.
Для нахождения ускорения звеньев второго контура надо взять производную
от системы уравнений 2.5 и в результате получим:
- L4cos(4)* (’4)2-L4 sin(4)* ’’4- L3cos(3)* (’3)2- L3 sin(3)* ’’3-b’’=0 2.5
-L4sin(4)* (’4)2+L4cos(4)* ’’4- L3sin(3)* (’3)2+ L3 cos(3)* ’’3=0
Если мы из каждого угла вычтем угол 4 , то получим:
- L4cos(4-4)* (’4)2-L4 sin(4-4)* ’’4- L3cos(3-4)* (’3)2- L3 sin(3-4)* ’’3-b’’=0
-L4sin(4-4)* (’4)2+L4cos(4-4)* ’’4- L3sin(3-4)* (’3)2+ L3 cos(3-4)* ’’3=0
и она принимает вид:
- L4 (’4)2- L3cos(3-4)* (’3)2- L3 sin(3-4)* ’’3-b’’=0
L4 ’’4- L3sin(3-4)* (’3)2+ L3 cos(3-4)* ’’3=0
Из этой системы уравнений находим ускорение ползуна b’’ и угловое ускорение
шатуна ’’4.
b’’=-L4 (’4)2- L3cos(3-4)* (’3)2- L3 sin(3-4)* ’’3
’’4= (L3sin(3-4)* (’3)2- L3 cos(3-4)* ’’3)/ L4=0
Подробные расчёты приведены в приложении.
Находим ускорения центра масс звеньев механизма.
Для нахождения ускорения центра масс звеньев надо взять производную от
систем уравнений, скоростей центра масс звеньев и в результате получим:
Ускорение центра масс звена 3:
S’’3x= -’’3L3sin(3-)/2 – (’3)2L3 cos(3-)/2
S’’3y= ’’3L3 cos(3-)/2-+ (’3)2L3sin(3-)/2
S ’’4x=[ Ls4(-’’4sin(4-) – (’4)2 cos(4-)) – L3(’’3sin(3-) + (’3)2 cos(3- ))]
S’4y=[ Ls4(-’’4cos(4-) – (’4)2 sin(4-)) – L3(’’3cos(3-) + (’3)2 sin(3-))]