4.5. Другие теоремы.

Теорема 5. О непротиворечивости.

Любое выполнимое множество формул является непротиворечивым.

Ф – выполнимо Ф – непротиворечиво

Доказательство:

( от противного)

Пусть Ф – выполнимо, но противоречиво 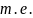найдется формула ψ, для которой можно вывести противоречие.

Ф ⊢ (ψ & ¬ψ) существует некая конечная последовательность формул 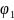, , 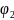…, ψ & ¬ψ Ф¹=Ф 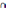{ ,…, 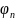} ⊢ ψ & ¬ψ //по теореме о дедукции// ⊢ (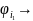 …( (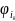ψ & ¬ψ)…)

Но т.к. любая доказуемая формула является общезначимой //по теореме о полноте//

( …( (ψ & ¬ψ)…) //по теореме импликации и следовании// … 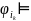ψ & ¬ψ

(связаны отношением следования)

Т.к. (ψ & ¬ψ)^I=Л => (Ф¹) =Л – невыполнимо Ф – невыполнимо. Противоречие! Ф – выполнимо и непротиворечиво.

Теорема 6. Теорема Мальцева (теорема компактности).

Если множество выполнимо, то выполнимо любое его конечное подмножество.

Ф – выполнимо S – выполнимо, S Ф и S – конечно.

Необходимость: Доказательство тривиально.

Достаточность:

Предположим, что все S- выполнимы, а Ф – невыполнимы Ф – противоречиво ( по теореме о выполнимости) найдется такая формула ψ, для которой Ф ⊢ ψ & ¬ψ (вывод всегда конечен) S Ф , S – конечно, S ⊢ ψ & ¬ψ S является противоречивым, S не выполнимо. Противоречие! Ф – выполнимо.

Теорема 7. Об адекватности.

Если формула ϕ следует из множества формул Ф, то формула ϕ выводится из Ф.

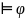Ф Ф ⊢

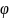
Необходимость:

Ф 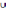{¬ } – невыполнимо противоречиво найдется такая формула ψ, что можно вывести и ψ и ¬ψ т.е. Ф, ¬ψ ⊢ ψ и Ф, ¬ψ ⊢ ¬ψ Ф ⊢ .

Достаточность:

Уже доказывали (теорема 1) Ф ⊢ Ф

Семантический и синтаксический подходы эквивалентны как в исчислении предикатов, так и в исчислении высказываний.

5. Алгоритмические модели.

5.1. Понятие алгоритма.

Алгоритм – конечная последовательность шагов, приводящая к получению результата из исходных данных.

Такое определение алгоритма является интуитивно ясным, но не определяемым понятием.

Проблемы, которые подвели к проблематике алгоритмов:

1. Алгоритмическая разрешимость. Имеет ли данная задача алгоритм решения?

2. Наибыстрейший алгоритм решения. Определение нижней границы сложности решения.

В рамках интуитивного определения алгоритма нельзя разрешить данные алгоритмические проблемы, поэтому рассмотрим, что именно в интуитивном понятии алгоритма нуждается в уточнении.

1. Что такое данные (алгоритмический объект)

2. Память. Способ хранения и представления данных

3. Элементарное действие, команда

4. Последовательность порождения операций, шагов

5. Что есть результат

6. Способ реализации

В теории алгоритмов принят подход, основанный на конкретной алгоритмической модели. Алгоритмическая модель – подкласс алгоритмов, в которых строго определены понятия алгоритма. При этом используемые алгоритмические модели универсальны (это недоказуемое утверждение) т.е. алгоритм в любой разумной алгоритмической модели имеет аналог в рамках данной.

Различают 3 класса алгоритмических моделей:

1. Класс как описание некоторого технического устройства: машина Тьюринга, машина прямого доступа, машина Поста.

2. Описание алгоритма как некоторого класса функций с определенными способами их образования: частично рекурсивные функции (исторически первая формализация понятия алгоритма).

3. Набор правил по преобразованию слов: алгорифм Маркова.