3.Определение периодичности диагностирования аналитическим методом

Периодичность l' диагностирования определяют аналити­чески. Условие этой технико-экономической задачи сформули­руем так: периодичность Г оптимальна в том случае, если ко­эффициент технической готовности максимален или затраты минимальны.

Чтобы определить оптимальную периодичность диагности­рования, необходимо решить задачу минимизации удельных затрат. Запишем выражение для удельных затрат и приравня­ем производную этого выражения к нулю.

Оптимальный режим диагностирования при установленной периодичности : l' получим из условия

{ }=M[V(l´)]dM[U(l´) - M[U(l´)]dM[V(l´)]=0,

где М [U (/')] — математическое ожидание затрат на обслужива­ние и ремонт; M[V(l')] — математическое ожидание длительности работы системы между профилактическими или ремонтными воз­действиями.

Запишем в общем виде уравнение для определения оптимальной периодичности диагностирования по наработке [9]:

(14)

Здесь λ(/') — интенсивность отказов; F (/') — функция распреде­ления пробега между отказами; С_пр— затраты при выполнении плановой диагностики и обслуживания (профилактики); С_т._р — затраты на выполнение внеплановых текущих ремонтов; l' — искомая оптимальная периодичность диагностирования.

Полученное уравнение имеет решение при любых законах распределения F(l). Для экспоненциального закона распределения F(l). для экспонинцеального закона распределения F(l)=1- последнее уравнение приобретает вид

При законе Вейбулла F(l)= 1- уравнение выражается следующим образом:

(16)

(𝜷, 𝜶— параметры закона Вейбулла).

Лекция№16 Графические методы определения оптимальной периодичности диагностирования

1.Применение графического метода для нормального закона распределения и закона распределения по Вейбуллу.

2. Применение графического метода для экспоненциального закона распределения.

3. Определение оптимальной периодичности диагностирования с учетом категории транспорта

Полученные уравнения для определения оптимальных режи­мов диагностирования справедливы для всех агрегатов, ме­ханизмов и узлов, кроме обеспечивающих безопасность дви­жения. Для этих систем нельзя устанавливать оптимальные режимы обслуживания только по минимуму удельных потерь.

Там, где речь идет о безопасности, экономической стороне проблемы принадлежит второстепенная роль, и задача должна решаться с учетом обеспечения заданного уровня вероятности безотказной работы.

П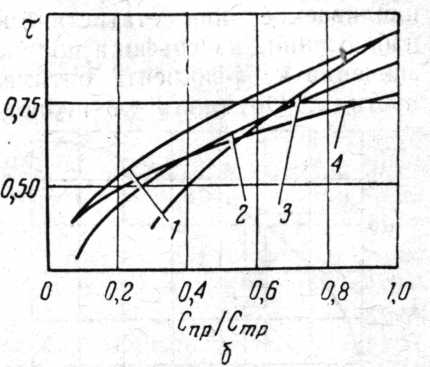 рактически бесконечно близко к вероятности безотказной работы, равной единице, можно приблизиться, если ежедневно производить принудительное обслуживание и замену отдель­ных элементов, влияющих на безопасность и склонных к отказам. Это практически неосуществимо. Следовательно, необходимо искать иные пути к достижению высокой вероятности безотказной работы.

Применение высокопроизводительных и эффективных контрольно-диагностических средств позволяет предложить метод обслуживания систем, обеспечивающих безопасность, который позволяет получить высокую вероятность безотказной работы при минимальных затратах средств на осуществление данной стратегии. Этот метод обслуживания состоит в принудитель­ном диагностировании технического состояния систем и их эле­ментов, обслуживании и ремонте в объеме, выявленном при диагностировании, и принудительной замене элементов в слу­чае достижения предельных значений выходных или структур­ных параметров.

Таким образом, применение экспресс-диагностирования с по­следующим обслуживанием и принудительной заменой через определенный пробег отдельных элементов системы позволит предупредить возникновение как износовых, так и внезапных отказов. Периодичность экспресс-диагностирования с достаточ­ной точностью определяется из кривой надежности, если задаться определенным уровнем безотказной работы при условии, что всякий раз после диагностирования полностью восстанавливает­ся техническое состояние системы и надежность становится близкой к единице.