Интенсивность отказов

λ(l) = f(l)/Р(l) = λе ^-λl/е ^–λl = λ = const.

Средняя наработка до отказа

l_ср = 1/λ.

Интенсивность отказов λ для различных механических элементов изменяется в широких пределах: (0,01—10)·10^-6 1/ч[35]. Например, для редукторов зубчатых λ = (0,01—0,20)·10^-6, для роликовых подшипников λ = (0,02—1,0) ·10^-6, для шарико­вых подшипников λ = (0,02—2,20)·10^-6, для муфт электромаг­нитных λ = (0,25 — 0,90) ·10^-6 1/ч.

3. Плотность двухпараметрического распределения Вейбулла

,

где α, β – параметры распределения.

Интегральная функция распределения отказов

.

Функция безотказной работы

.

Интенсивность отказов

.

Распределение Вейбулла занимает особое место при оценке вероятности безотказной работы многих деталей и узлов автомобилей.

С помощью распределения Вейбулла можно описать самые разнообразные случаи отказов. Если β < 1, распределение имеет вид убывающей функции. При β = 1 распределение Вейбулла совпадает с экспоненциальным. В случае β = 3,3 распределение Вейбулла близко к нормальному закону распределения.

Между статистическими и теоретическими распределениями возможны некоторые расхождения. Поэтому для проверки их согласованности используются специальные критерии оценки ( а) χ² или Пирсона и б) Колмогорова).

а)При определении согласия по критерию χ ² определяют вероятность согласия теоретического и статистического распределений. Если вероятность более 0,05, статистическое распределение согласуется с теоретическим, если меньше 0,05, выбранный теоретический закон распределения отвергается.

б)Критерий Колмогорова проще критерия χ ², но дает завышенное значение вероятности согласия.

в) Можно закон распределения выбирать и по коэффициентам вариации (ГОСТ 37.001.043 —72).

Для нормального распределения коэффициент вариации

υ = σ/l_ср

может изменяться в пределах 0,08—0,40,

для распределения Вейбулла и логарифмически нормального

– от 0,35 до 0,85 и

для экспоненциального распределения он равен 1.

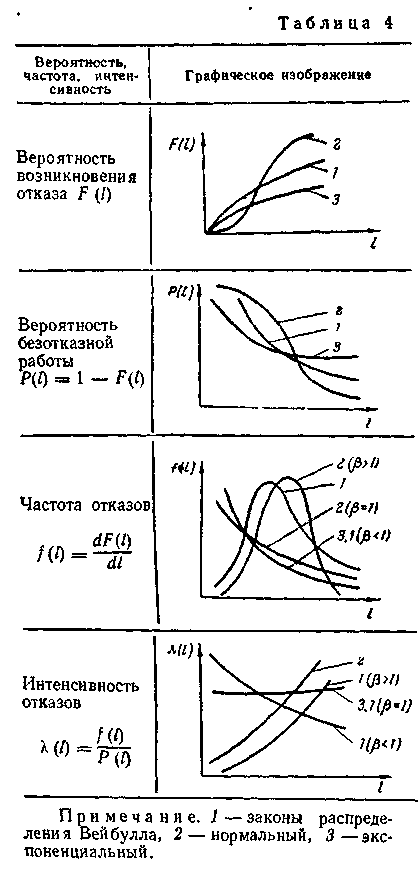
Из приведенных графиков основных законов распределения отказов (табл. 4) видно, что при нормальном законе распределения интенсивность отказов с возрастанием пробега монотонно и неограниченно возрастает. Интенсивность отказов неограниченно растет и при распределении Вейбулла.

Для β = 1 интенсивность отказов λ (l) = α, т. е. является постоянной величиной и совпадает с интенсивностью экспоненциального распределения.

В случае β > 1 интенсивность отказов неограниченно возрастает до бесконечности.

При β < 1 она с возрастанием пробега убывает до нуля. Распределение Вейбулла при значении параметра β < 1 приемлемо для описания явлений приработки.

Из механизма возникновения отказов следует, что накопление внешней энергии объектом и соответственно процесс снижения его прочности происходят непрерывно с самого начала эксплуатации. Нагружение объекта внешними случайными нагрузками происходит также непрерывно и одновременно с накоплением общей энергии объектом, т. е. механизм возникновения постепенных и внезапных отказов действует одновременно и непрерывно.

В связи с этим при оценке надежности объекта необходимо в общем случае учитывать одновременное действие внезапных и постепенных отказов.

Тогда надежность в условиях совместного действия внезапных и постепенных отказов выразится произведением вероятности безотказной работы при внезапных отказах и вероятности безотказной работы при износовых отказах:

Если пренебречь периодом приработки и принять надежность в начальный момент равной единице, тогда с учетом того, что действие износных отказов сдвинуто вправо по сравнению с внезапными (т. е. износные отказы проявляются позднее), кривая надежности будет иметь вид, представленный на рис. 4. До некоторого момента общая кривая надежности совпадает с кривой надежности экспоненциального закона. До этого момента можно считать распределение отказов подчиняющимся экспоненциальному закону, а этап эксплуатации — нормальным. После некоторого момента вступают в силу износные отказы и кривая надежности резко падает. Этот этап можно считать этапом износных отказов. Такое разделение этапов возникновения отказов справедливо не только для элементов, но и для систем, так как любая система состоит из некоторой совокупности элементов.

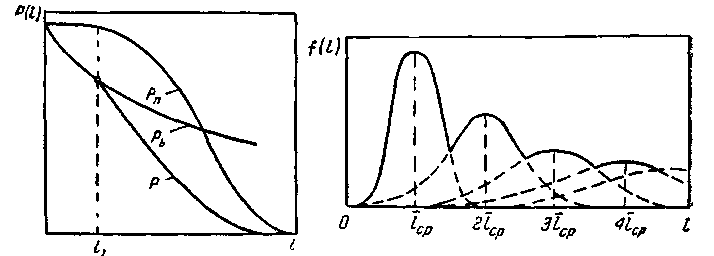
Рис. 4. Кривые надежности с учетом внезапных и постепенных отказов

Рис. 5. Схема стабилизации потока отказов

Лекция10 Изменение показателей безотказности в процессе эксплуатации восстанавливаемых объектов