3.Показатели основных характеристик надежности.

П од безотказностью понимают свойство изделия сохранять непрерывную работоспособность.

В дальнейшем будем делить изделия на невосстанавливаемые восстанавливаемые.

Показателями безотказности невосстанавливаемых изделий (например, зубчатых колес) являются вероятность безотказной работы, средняя наработка до отказа и интенсивность отказа.

Показатели восстанавливаемых изделий несколько другие: вероятность безотказной работы, наработка на отказ, характеристика и параметр потока отказа. При возникновении отказов детали восстанавливаются и продолжают работать.

Рассмотрим показатели безотказности невосстанавливаемых деталей.

Показатели безотказности невосстанавливаемых деталей можно определить, если будут известны: плотность (вероятностно-дифферен-циальная форма записи) распределения времени работы изделия до отказа f(l), интегральная форма закона распределения времени работы изделия до отказа F(l) и вероятность безотказной работы Р(/) (рис. 2). Эти функции распределения связаны между собой зависимостями f (1) = dF (1)/ dl,

P(l)=1 — F (l). Можно также записать, что f (х) = - dP (1)/ dl.

Продолжительность работы изделия (километры, часы, число циклов)

оценивается наработкой. Средняя наработка до отказа определяется из выражения

.

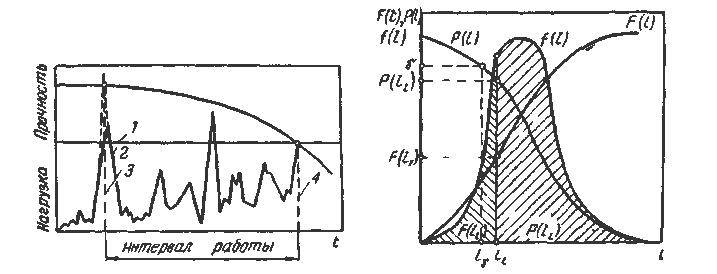
Рисунок 1. Схема возникновения отказа:

1 — постоянная нагрузка;

2 — случайный характер нагружения;

3 — внезапный отказ;

4 — нзносовый отказ

Рисунок 2. Кривые распределения отказов, вероятности безотказной работы и плотности вероятности

Среднее квадратическое отклонение

Интенсивность отказа

λ(l) = f(1)/Р(l) (8).

При малой наработке интенсивность отказов приближенно равна

ΔN/ΔlN,

где ΔN — число отказавших изделий за наработку Δl,

N — число работоспособных изделий к началу рассматриваемой наработки.

Один из основных показателей безотказности восстанавливаемых изделий — параметр потока отказов ω(/). Его размерность определяется размерностью наработки (км^-1, ч^-1).

При стационарном ординарном потоке без последействия интенсивность отказов λ(l) для невосстанавливаемых изделий и параметр потока отказов ω(1) для восстанавливаемых изделий совпадают. Наработку на отказ (среднее время безотказной работы) находим из простого выражения:

l = 1/ω

Показатели долговечности

К показателям долговечности («прочности, развернутой во времени») относятся следующие:

ресурс (срок службы) или наработка -(продолжительность эксплуатации) от определенного момента време­ни до выхода изделия в предельное состояние или до списания;

гамма-процентный ресурс, т. е. срок службы, который имеет обу­словленное число (γ) процентов данных изделий и превышает его (γ % — вероятность долговечности, а l_γ — соответствующая ей наработка, например l_γ = l₉₀ = 150 тыс. км);

средний ресурс — среднее значение срока службы, определяемое по совокупности изделий; ресурс до первого капитального ремонта.

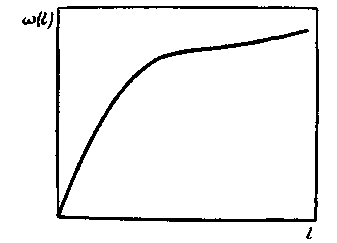Рис. 3. Изменение параметра

потока отказов

Показатели ремонтнопригодности

К показателям ремонтопригодности относятся:

Вероятность восстановления и среднее время ремонта.

Вероятность восстановления работоспособности в заданное время t определяется по формуле:

,

где — плотность распределения времени восстановления.

Если через п (t) обозначить число восстанавливаемых изделий и через N— число работоспособных изделий, при статистической оценке

Показателисохраняемости

К показателям сохраняемости (при хранении или транспортировке изделий) относятся безотказности при хранении и средний срок сохраняемости за промежуток времени от t₁ до t₂:

,

где f_o(t)—плотность распределения работоспособности при хранении.

Комплексные показатели готовности изделий

Существуют комплексные показатели готовности изделий.

К ним относятся коэффициент готовности и коэффициент технического использования.

Коэффициент готовности характеризует вероятность работоспособности изделия в произвольный момент времени

K_Г = T₀/(T₀ + Tc),

где T₀ — наработка на отказ, Т_с — среднее время восстановления.

Коэффициент технического использования

Т_Т.И = t_сум/(t_сум + t_p + t_об).

Здесь t_сум — суммарная наработка; t_p — суммарный простой в плановых и неплановых ремонтах, t_об — суммарное время простоя в техническом обслуживании.

Показатели, используемые в автомобильном транспорте

На автомобильном транспорте применяются такие коэффициенты: технической готовности, выпуска подвижного состава и использования парка.

Коэффициент технической готовности

,

где АД_Т — автомобиле – дни нахождения автомобилей в технически исправном состоянии; АД_И – автомобиле – дни инвентарные; АД_р – автомобиле – дни нахождения в ремонте (обязательные работы, диаг­ностирование, устранение неисправностей).

Коэффициент выпуска подвижного состава

,

где АД_Э – автомобиле-дни нахождения в эксплуатации; АД_Н – автомобиле-дни нормированных простоев (число выходных и праздничных дней, в которые парк не работает). Коэффициент использования парка

Лекция 9 Основные виды законов распределения случайных величин для сервиса и технической эксплуатации автомобилей.

1. Законы распределения случайных величин.

2. Закон распределения Вейбулла (ЗРВ)

3. Нормальный закон распределения Гаусса (ЗНР)

4. Экспоненциальный закон распределения (ЭЗР)

1.Законы распределения случайных величин.

При исследовании надежности и определении сроков службы машин применяются различные статистические модели (законы распределения) случайных величин. Исследованиями установлено [35], что применительно к автомобилям можно принять следующую распространенность разных законов распределения случайных величин: Вейбулла – 55 – 60%, нормальное (Гаусса) – 35 – 40%, экспоненциальное и логнормальное – 4 – 6%.

Имея эмпирическую плотность распределения (гистограмму), с помощью математических методов находим статистическую модель (закон распределения) случайных величин. Можно также решить обратную задачу: по статистической модели определить характеристики надежности изделия, вероятность появления отказов и другие показатели. При выборе закона распределения недостаточно одного формального сходства гистограммы с законом распределения. Необходимо также учитывать физику явления, т. е. стремиться к рассмотрению полной модели отказов.

1. Распространенной статистической моделью является нормальное (гауссово) распределение.

При большом числе наблюдений законы распределения приближаются к нормальному. По нормальному закону изменяются износы и другие постепенные отказы, периодичности ТО-1 и ТО-2, периодичности отказов автомобилей, двигателей и других узлов.

Плотность нормального распределения определяем по формуле

,

где l – любое значение ряда распределения;

lср – математическое ожидание (среднее значение, центр распределения);

σ – среднее квадратическое отклонение случайной величины l.

Интегральную функцию нормального распределения отказов и функцию безотказной работы запишем в виде

.

Здесь Ф(z) – нормированная функция нормального распределения, в которой принимается новая случайная величина (нормированное отклонение) . В формуле , при l = l_ср, z = 0.

Таким образом, при нормировании начало координат переносится в точку l = l_ср и абсцисса выражается в долях среднего квадратического отклонения σ.

В целях облегчения расчетов для нормированных функций распределения в дифференциальной и интегральной формах составлены специальные таблицы.

Например, если необходимо определить вероятность замены данного узла в случае пробега автомобиля с начала эксплуатации 100 тыс. км при средней наработке до отказа l_ср = 124 тыс. км и среднеквадратическом отклонении σ = 30 тыс. км, то рассчитав нормированное отклонение , из таблицы получим Ф(-0,80) 0,29. Это значит, что 21 % автомобилей потребуют замены данного узла при пробеге до 100 тыс. км.

Одна из важных характеристик нормального распределения — «правило трех σ», из которого следует, что практически все случайные величины (99,9 %) лежат в интервале ±3σ.

2. Для описания событий, которые возникают с постоянной интенсивностью и независимо друг от друга, служит однопараметрическое экспоненциальное распределение.

Этим законом описываются внезапные отказы, наработки между отказами, трудоемкости текущего ремонта и т. д.

Плотность распределения отказов определяется по формуле

f(l) = λe^-λl.

Интегральная функция распределения отказов

F(l) = 1 - e^-λl,

а функция безотказной работы

Р(l)= - e^-λl.