30. Прохождение синусоидального тока через конденсатор
И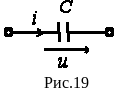
деальный
емкостный элемент не обладает ни активным
сопротивлением (проводимостью), ни
индуктивностью.
Если
к нему приложить синусоидальное
напряжение
(рис.19), то ток i
через
него будет равен
Полученный
результат показывает, что напряжение
на конденсаторе отстает по фазе от тока
на
:
.
Таким образом, если на входы двухлучевого
осциллографа подать сигналы u
и i,
то на его экране будет иметь место
картинка, соответствующая рис.20.
Из
полученной формулы вытекает закон Ома
для амплитудных и действующих значений
напряжения и тока:
;
.
Введенный
параметр
называют
реактивным
емкостным сопротивлением конденсатора.
Как и резистивное сопротивление, ХС имеет
размерность Ом.
Однако данный параметр является функцией
частоты, что иллюстрирует рис. 73. Из рис.
73 видно, что при f=0
конденсатор
представляет разрыв для тока, а при f
ХС=0.
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
,
разделим первый из них на второй:
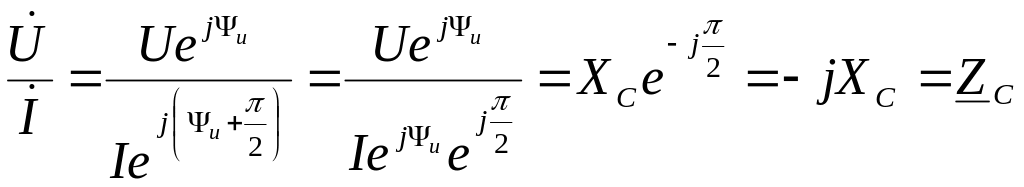
или (закон Ома в комплексном виде)
(*).
В
последнем соотношении
–
комплексное сопротивление конденсатора.
Умножение на
соответствует
повороту вектора на угол /2 по
часовой стрелке. Следовательно, уравнению
(*) соответствует векторная диаграмма,
представленная на рис. 74.
Здесь
сдвиг фаз между напряжением и током
.
Поэтому для мгновенного значения
мощности можно записать
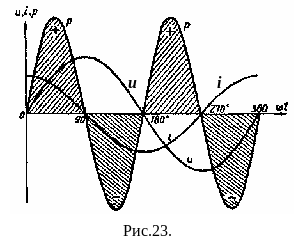
Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
31. Последовательные соединения r и l элементов .
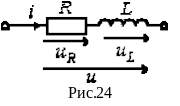
1) Как указывалось в параграфе 25, катушка любого электротехнического устройства обладает определенным активным сопротивлением R и индуктивностью L. Участок с индуктивностью L будем рассматривать как участок, обладающий индуктивным сопротивлением ХL.
Пусть
ток в ветви на рис.24 
.
Тогда
.
Здесь
,
,
.
– сдвиг фаз между током и напряжением. Пределы изменения : 0< < /2, т.е. в этом случае напряжение всегда опережает ток.
Полученному уравнению можно поставить в соответствие соотношение:
.
где
– полное сопротивление.
Полученным выражениям соответствует векторная диаграмма на рис. 77 (треугольник напряжений) и треугольник сопротивлений (рис. 78). Треугольники подобны.
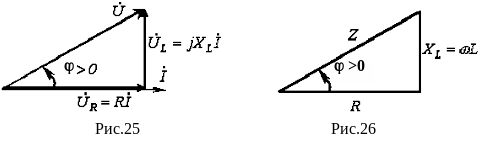
Угол сдвига по фазе между напряжением и вызванным им током можно определить из соотношения:
.
График
p(t)
(где
)
показывает, что активная мощность
непрерывно поступает из сети и выделяется
в активном сопротивлении в виде теплоты.
Она равна
.
Мгновенная мощность, обусловленная энергией магнитного поля индуктивности, циркулирует между сетью и катушкой. Ее среднее значение за период равно нулю:
