Построение эпюр поперечных сил и изгибающих моментов

Для расчета балки на прочность при изгибе, необходимо знать наибольшие значения поперечной силы и изгибающе­го момента и положение сечений, в которых они действуют. В связи с этим возникает необходимость определения законов изменения и по длине балки. Для этой цели обычно стро­ят эпюры поперечных сил и изгибающих моментов, которые пред­ставляют собой графическое изображение функций и .

Примем положительное направление оси Оу вниз. При этом на эпюре положительные ординаты будем откладывать вниз, а отрицательные — вверх. Ординаты эпюры будем отклады­вать со стороны растянутых волокон балки. Согласно этому правилу для балок положительные значения изгибающих мо­ментов откладываются вниз, так как эти моменты вызывают ра­стяжение нижних волокон.

Рассмотрим пример построения эпюр и

Пример 1. Построим эпюры и для шарнирно опертой балки, показанной на рис. 6.14.

Из уравнений статики найдем опорные реакции:

.

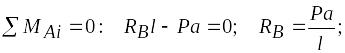
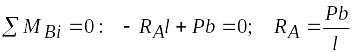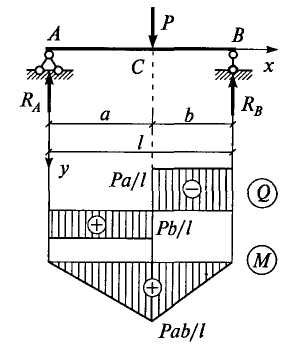
Рис. 6.14

Установим законы изменения и на участках АС и СВ балки.

На участке АС ( )

.

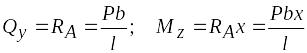На участке СВ ( )

.

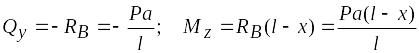Из полученных выражений видно, что поперечная сила на участках АС и СВ имеет постоянное значение, а в точке С име­ет скачок, равный Р.

Изгибающие моменты изменяются по линейным законам, при этом в точках А и В = 0, а в точке С = Pab/l. Эпюры и показаны на рис. 6.14.

3. Нормальные напряжения при чистом изгибе

Рассмотрим участки балки, в пределах которых изгибающий момент имеет постоянное значение ( = const), а поперечная сила отсутствует ( = 0). Такой изгиб принято называть чис­тым изгибом. Для балки, показанной на рис. 6.15, это имеет ме­сто в пределах участка CD.

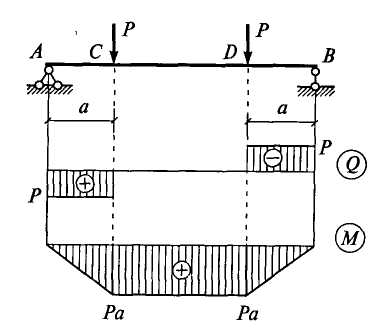
Рис. 6.15

Установим закон распределения напряжений в поперечном се­чении балки при чистом изгибе. Характер деформации балки мож­но исследовать с помощью опыта на резиновой модели прямоу­гольного сечения с нанесенной на боковых гранях ортогональной сеткой в виде продольных и поперечных прямых линий (рис. 6.16, а). После деформирования на участке чистого изгиба продольные прямые принимают криволинейное очертание, а по­перечные — остаются прямыми (рис. 6.16, б). При этом сетка оста­ется ортогональной. Отсюда можно сделать вывод, что угловые де­формации в плоскости изгиба отсутствуют и поперечные сечения балки при деформации не искривляются, а остаются плоскими.

Рис. 6.16

Из рис. 6.16, б видно, что продольные волокна балки, распо­ложенные ниже некоторого слоя, испытывают растяжение, а выше этого слоя — сжатие. Такой слой называется нейтральным слоем. Волокна этого слоя не удлиняются и не укорачиваются. Следовательно, ниже нейтрального слоя в поперечных сечени­ях действуют растягивающие нормальные напряжения, а выше этого слоя — сжимающие напряжения. Линия пересечения ней­трального слоя с плоскостью поперечного сечения называется нейтральной осью (нулевой линией) сечения.

Экспериментальные и теоретические исследования чистого изгиба балок дают основание принять следующие гипотезы.

1. Поперечные сечения балки, плоские до деформации, остают­ся плоскими и ортогональными к нейтральному слою после дефор­мации (гипотеза Я. Бернулли). Эта гипотеза равносильна пред­положению о том, что при изгибе происходит поворот попереч­ных сечений на некоторый угол относительно нейтральной оси и что угловые деформации в продольных сечениях балки отсут­ствуют.

2. Взаимное давление между продольными слоями отсутству­ет. Из этого следует, что продольные волокна находятся в усло­виях одноосного растяжения или сжатия.

Рассмотрим чистый изгиб стержня произвольного попереч­ного сечения. Поместим начало координат в произвольной точ­ке О поперечного сечения (рис. 6.17), направив ось Ох парал­лельно оси стержня, а ось Оу — вертикально вниз.

Предположим, что силовая плоскость, в которой действует изгибающий момент М, не совпадает с координатными плоско­стями Оху и Oxz.

Из гипотезы плоских сечений (гипотеза 1) следует, что пере­мещение и произвольной точки К поперечного сечения вдоль оси Ох является линейной функцией координат y и z точек по­перечного сечения и может быть представлено в виде

, (6.6)

где и — углы поворота сечения относительно взаимно перпендикулярных осей Оу и Oz (рис. 6.18, б, в). Эти величины яв­ляются функциями переменной х. Поступательное перемещение плоскости поперечного сечения в направлении оси Ох отсут­ствует.

Рис. 6.17

Продольные волокна стержня испытывают одноосное растя­жение или сжатие (гипотеза 2). Используя формулу

,

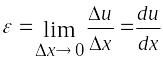определим относительное удлинение продольного волокна, проходящего через произвольную точку К поперечного сечения.

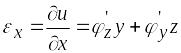. (6.7)

Рис. 6.18

Здесь линейная деформация определяется как частная произ­водная перемещения и, так как оно является функцией трех пе­ременных х, у и z.

Из закона Гука при одноосном растяжении или сжатии полу­чим

. (6.8)

Изгибающий момент М, действующий в силовой плоскости, можно разложить на два момента и , действующие в плоскостях Оху и Oxz (рис. 6.18, а).

Внутренние усилия в сечении стержня связаны с напряжени­ями соотношениями.

. (6.9)

Подставляя в эти соотношения выражение ох из (6.8) и учи­тывая, что при изгибе продольная сила N = 0, получим следу­ющую систему уравнений относительно неизвестных и :

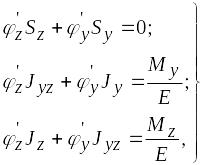(6.10)

где — статические моменты площади относительно осей Оу и Oz:

.

— осевые и центробежный моменты инерции:

.

Если оси Оу и Oz являются главными центральными осями поперечного сечения, то , и из (6.10) находим

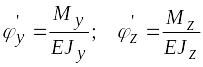. (6.11)

Подставив эти величины в (8), получим

. (6.12)

Если силовая плоскость совпадает с главной плоскостью Оху (прямой изгиб), то = 0, и формула (6.12) принимает вид

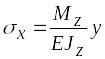. (6.13)

Таким образом, при чистом изгибе стержня в плоскости Оху нормальные напряжения в поперечном сечении стержня изменя­ются по линейному закону. Переменная у отсчитывается от главной оси Oz, которая является нейтральной осью (нулевой линией).

Из формулы (6.13) видно, что в точках нейтральной оси на­пряжения равны нулю, а наибольшие и наименьшие значе­ния они принимают в нижних ( ) и в верхних ( ) во­локнах, наиболее удаленных от нейтральной оси

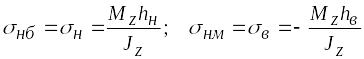. (6.14)

Эти формулы удобнее представить в виде

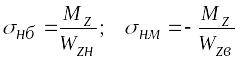. (6.15)

где

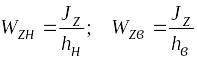. (6.16)

Величины и называются моментами сопротивления сечения для нижних и верхних волокон.

Характер эпюры нормальных напряжений для сечения, не симметричного относительно нейтральной оси, например, для таврового сечения при > 0, изображен на рис. 6.19.

Из приведенной на рис. 6.19 эпюры видно, что в балке с не­симметричным относительно нейтральной оси сечением наи­большие по абсолютной величине напряжения возникают в волокнах, наиболее удаленных от нейтральной оси.

Они могут быть определены по формуле

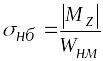, (6.17)

где — меньший из моментов сопротивления или .

Рис. 6.19

Для сечений, симметричных относительно нейтральной оси,

,

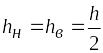и момент сопротивления определяется по формуле

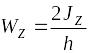. (6.18)

Напряжения в крайних волокнах в этом случае равны по ве­личине и определяются по формуле

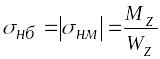. (6.19)

На рис. 6.20 изображен характер эпюры ох для прямоугольного, круглого и двутаврового сечений при M>0.

Моменты инерции и моменты сопротивления прямоугольно­го, круглого сплошного и кольцевого сечений определяются по следующим формулам:

для прямоугольного сечения:

; (6.20)

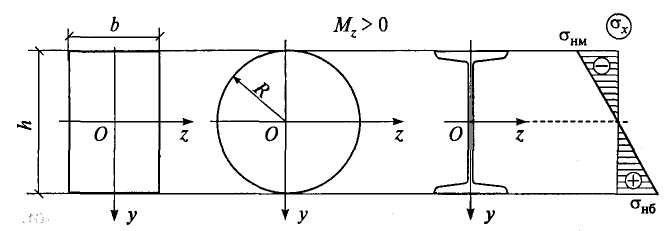
Рис. 6.20

для круглого сечения

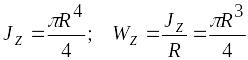; (6.21)

для кольцевого сечения с внутренним и внешним радиусами и

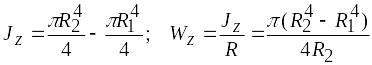; (6.22)

Для прокатных двутавров и швеллеров величины моментов инерции и моментов сопротивления приведены в сортаменте.