1. Намечаем характерные сечения.
2. Определяем поперечную силу в каждом характерном сечении.
По вычисленным значениям строим эпюру .
3. Определяем изгибающий момент в каждом характерном сечении.
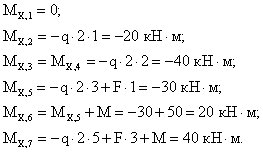
По вычисленным значениям строим эпюру , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
Пример 3.
Построить эпюры , (рис.6.19).
В данном случае для правильного построения эпюры необходимо использовать приведенные выше дифференциальные зависимости.
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечные силы в характерных сечениях.
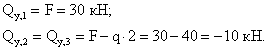
3. Строим эпюру .
Характер
эпюры, то есть тот факт, что эпюра
пересекает ось, говорит о том, что в этом
сечении момент
будет иметь экстремальное значение.
Действительно, пересечение эпюры с осью
z означает,
что в этом сечении
,
а из курса математики известно, что если
производная функции равна нулю, то сама
функция в данной точке имеет экстремальное
значение.
Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки :
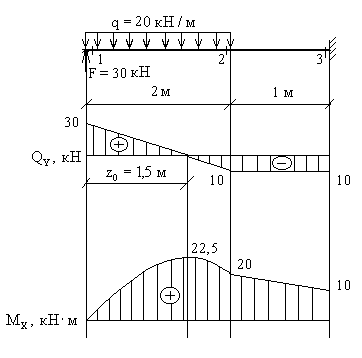
Рис. 6.19
Определяем изгибающие моменты в характерных сечениях.
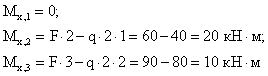
4. Вычисляем экстремальное значение изгибающего момента в сечении, где :
Строим
эпюру
.
Примеры построения эпюр внутренних силовых факторов для балок на двух опорах
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.
Для
плоской системы число уравнений статики
в общем случае равно трем. Если балка
загружена только вертикальными
нагрузками, то горизонтальная реакция
шарнирно-неподвижной опоры равна нулю,
и одно из уравнений равновесия
обращается в тождество. Таким образом,
для определения реакций в опорах
шарнирной балки используются два
уравнения статики:
Условие
используется для проверки вычисленных
значений опорных реакций.
Рассмотрим примеры построения эпюр Qy и Mx.
Пример 4.
z1
Для балки, изображенной на рис.6.20 построить эпюры поперечной силы Qy и изгибающего момента Mx и определить опасное сечение. Пусть величины P = 10 кН, a = 2 м, b = 3 м.
Решение.
Определим реакции опор. Запишем уравнения равновесия статики. Из этих уравнений получим:
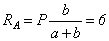кН.
кН.
Для проверки правильности определения реакции опор используем уравнение:
;
.
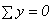6 – 10 + 4 = 0,
0 º 0.
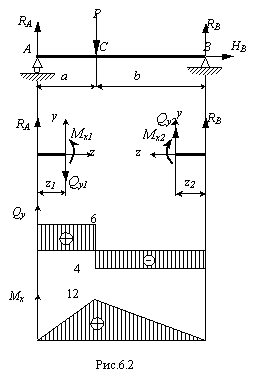
Рис.6.20
Значит, реакции определены правильно.
Определим внутренние усилия, возникающие в материале балки. Следует рассмотреть два участка, границами участков являются точки приложения сосредоточенной силы Р и опорных реакций RA и RB. Обозначим границы участков буквами А, С и В.
Рассечем первый участок АС.
Отбросим правую часть, т.к. она сложнее.
Заменим отброшенную часть внутренними усилиями Qy и Mx.
Уравновесим отсеченную часть, запишем уравнения равновесия:
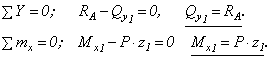
Вычислим Qy и Mx в граничных точках участка:
при z1 = 0, Qy1 = RA = 6 кН, Mx1 = 0;
при z1 = а = 2 м, Qy1 = RA = 6 кН, Mx1 = 12 кНм.
Рассмотрим второй участок СВ. Рассечем его и отбросим левую часть, заменим её внутренними силами. Из уравнений равновесия получим
Вычислим Qy и Mx в граничных точках участка:
при z2 = 0, Qy2 = - RВ = - 4 кН, Mx2 = 0;
при z2 = а = 3 м, Qy2 = - RВ = - 4 кН, Mx2 = 12 кНм.
Построим эпюры Qy и Mx.
По полученным эпюрам определим опасное сечение, оно проходит через точку приложения силы P, так как Mx достигает там наибольшего значения.
Пример 5.
Для представленной на рис.6.21 балки построить эпюры внутренних сил, найти опасные сечения.
Рис.6.21
Решение.
Определим реакции опор. Заменим распределенную нагрузку q её равнодействующей G=2qa, приложим G в середине участка АС (рис.6.22).
Запишем уравнение равновесия.
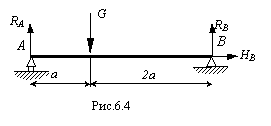
Рис.6.22
;
;
.
Отсюда находим:
;
.
Выполним проверку правильности определения реакций опор.
;
;
0 º 0.
Используя метод сечений, рассмотрим сечения участков балки (рис.6.23).
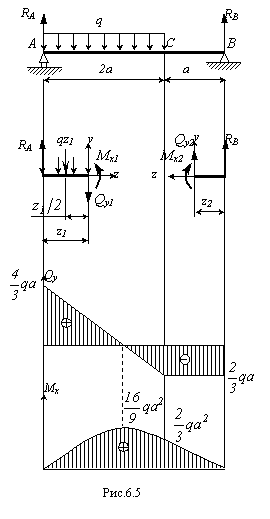
1 участок:
;
.
.
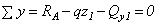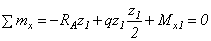
Вычислим Qy1 и Mx2 на границах участка.
,
,
;
,
,
;
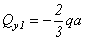2 участок:
;
.
;
.
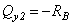На границах участка получим
,
,
;
,
,
;
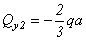Построим эпюры Qy и Mx на участках. Из выражений для внутренних усилий следует, что Qy, эпюра является прямолинейной как на первом, так и на втором участках, в то время как эпюра Мх на первом участке квадратичная парабола, а на втором прямая линия. Для построения эпюры Мх на первом участке следует либо вычислить её значения в нескольких точках, либо исследовать функцию на экстремум и определить его.
Как известно из курса математического анализа, для определения экстремума функции следует определить ее первую производную, приравняв ее нулю найти аргумент, затем его значение подставить в функцию и вычислить экстремум функции.
,
,
,
.
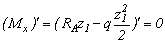Отложим
значение Мх
max
и построим эпюру изгибающего момента
на первом участке по трем точкам
(рис.6.23). По эпюре находим опасное сечение.
Им является сечение, где
.
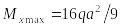Пример 6.
Построить эпюры , для балки с шарнирным опиранием (рис.6.24).
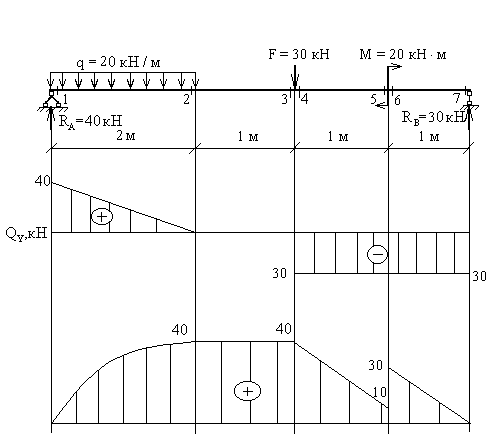
Рис. 6.24
Порядок расчета.
1. Вычисляем реакции опор.
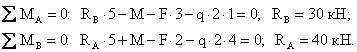
Проверка:
2. Намечаем характерные сечения.
В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.
3. Определяем поперечные силы в характерных сечениях.
Строим эпюру .
4. Определяем изгибающие моменты в характерных сечениях.
Строим эпюру
Пример 7.
Построить эпюры и для балки на двух опорах с консолью (рис.6.25,а)
Порядок расчета.
1. Вычисляем опорные реакции.
Во
втором уравнении равновесия (впрочем,
как и в первом) момент от распределенной
нагрузки
вычислен без разбиения ее на две части
- слева и справа от опоры В,
то есть определена равнодействующая
нагрузки
,
ее положение (в середине участка с
распределенной нагрузкой), что позволяет
определить плечо равнодействующей
относительно опоры В
и направление создаваемого ею момента.
В то же время можно было в уравнении
равновесия учитывать отдельно части
нагрузки
,
приложенные слева и справа от опоры В;
при этом второе уравнение равновесия
имеет вид:
Рис.6.25
Вычисленное
из этого уравнения значение реакции
,
разумеется, совпадает с полученным
ранее.
Проверка:
2. Намечаем характерные сечения.
3. Вычисляем поперечную силу и изгибающий момент в характерных сечениях.
Из рассмотрения левой отсеченной части:
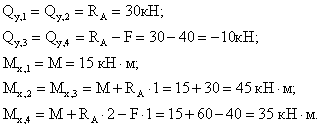
Для сечений 5-7 удобнее рассматривать правую отсеченную часть:
По
вычисленным значениям строим эпюры
и
(рис.6.25,б,в).