Задание 2

Доказать для произвольных множеств X,Y,W,Z справедливость (или несправедливость) следующих высказываний:

2.1)

2.2) ;

Теоретическая часть:

Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.

- пустое множество, множество, не содержащее ни одного элемента.

Множества равны, если они состоят из одних и тех же элементов.

Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.

X подмножество Y, если ;

X и Y равны

Множество, которое содержит все элементы, из которых состоит множество X, называется универсумом.

; ; ; ;

;

При доказательствах были использованы законы алгебры логики для простых и составных высказываний:

- логические утверждения, тогда:

; - идемпотентность

;

;

- закон противоречия

- закон исключения третьего

- закон двойного отрицания

; - законы де Моргана

; - коммутативность

; - ассоциативность

; - дистрибутивность

Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.

Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.

;

Операция декартовое произведение не коммутативна.

Практическая часть:

Доказательство 2.1:

2.1) Доказательство с помощью метода от противного:

Предположим, что:

Следовательно, наше предположение неверно. Т. о. равенство 2.1 выполняется.

Доказательство 2.2:

2.2)Доказательство взаимным включением:

1) Докажем, что: ; (*)

Дальнейшие рассуждения не возможны. Следовательно, (*) неверно.

2) Докажем, что:

ч.т.д.

Т. о. равенство 1.2 не выполняется, но примет вид .

Задание 3

Доказать или опровергнуть, что для множеств А,В,С, где причем справедливы высказывания:

3.1)

3.2) ;

Теоретическая часть:

Множество – совокупность некоторых вполне различимых элементов, объединенных каким либо свойством и мыслимых как единое целое.

- пустое множество, множество, не содержащее ни одного элемента.

Множества равны, если они состоят из одних и тех же элементов.

Два множества не равны, если в одном из множеств есть элемент, не принадлежащий другому множеству.

X подмножество Y, если ;

X и Y равны

Множество, которое содержит все элементы, из которых состоит множество X, называется универсумом.

; ; ; ;

;

Множество всех подмножеств I и операции и образуют алгебру подмножеств множества I.

выполняется:

Идемпотентность: ;

Коммутативность: ;

Ассоциативность: ;

Дистрибутивность: ;

Поглощение:

При доказательствах были использованы законы алгебры логики для простых и составных высказываний:

- логические утверждения, тогда:

; - идемпотентность

;

;

- закон противоречия

- закон исключения третьего

- закон двойного отрицания

; - законы де Моргана

; - коммутативность

; - ассоциативность

; - дистрибутивность

Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.

Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.

;

Операция декартовое произведение не коммутативна.

;

Операция проектирования справедлива для множеств, элементами которых являются кортежи одинаковой длины.

Операция проектирования множества, состоящего из кортежей - операция выделения первых, вторых и т. д. компонент кортежей и образование из них нового множества.

;

Композиция применима к упорядоченным множествам, состоящим из двоек.

y – компонирующий элемент.

Пусть ; .

Инверсией кортежа называется и через обозначается кортеж , где , а .

Инверсия произвольного множества состоит из его пар и обозначается . Следовательно, для любого произвольного кортежа справедливы высказывания:

;

;

.

Практическая часть:

Доказательство 3.1:

3.1)Доказательство взаимным включением:

1. Докажем, что:

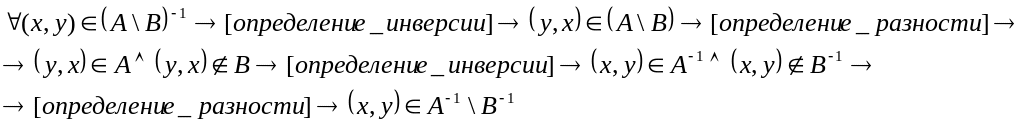ч.т.д.

2. Докажем, что:

ч.т.д.

Т. о. равенство 3.1 выполняется.

Доказательство 3.2:

3.2)Доказательство взаимным включением:

1. Докажем, что:

Т.к. пересечение включено в объединение , то выполняется.

2. Докажем, что:

Дальнейшие рассуждения не имеют смысла, так как в выражении 2 разных компонирующих элемента, следовательно данное выражение не возможно представить в ином виде. Обратное включение не выполняется.

Т. о. утверждение 3.2 верно.