- •Глава 1. Состояние вопроса и задачи исследования
- •1.2. Физические свойства семян овса и овсюга и их анализ
- •1.3. Способы очистки семян овса от овсюга
- •1.3.1. Механические способы очистки
- •1.3.2. Электрические способы очистки
- •1.4. Анализ теоретических положений поведения вытянутых частиц на плоскости в электростатическом поле
- •1.5. Задачи исследования
- •1. Лента-решето. 2. Потенциальный электрод. 3. Слой диэлектрика.
- •4. Загрузочный бункер. 5. Овсюг и легкие семена овса. 6. Бункер отходов.
- •7. Очищенная фракция семян. 8. Самотек чистых семян.
- •3.4. Лабораторная экспериментальная установка и методика исследования выделения овсюга из семян овса
- •1. Диэлектрическая кассета. 2. Решето с круглыми отверстиями. 3. Стойка ограничивающая.4. Крышка.5. Лабораторная экспериментальная установка.
- •6. Кронштейн. 7. Основание. 8. Уравновешивающий груз
- •3.5. Методика поиска оптимальных режимов выделения овсюга из овса
1. Диэлектрическая кассета. 2. Решето с круглыми отверстиями. 3. Стойка ограничивающая.4. Крышка.5. Лабораторная экспериментальная установка.
6. Кронштейн. 7. Основание. 8. Уравновешивающий груз
3.5. Методика поиска оптимальных режимов выделения овсюга из овса
Математические методы планирования эксперимента позволяют значительно повысить производительность труда при исследовании за счет значительного сокращения числа опытов, а стало быть, времени и средств на их проведение [3]. Кроме этого исследователь имеет возможность получить математическую модель процесса и оптимальный режим. Поэтому для нахождения оптимального режима работы лабораторной экспериментальной установки и опытной полупроизводственной установки решена многофакторная экспериментальная задача.
Качество работы электросемяочистительных машин в зависимости от материала, подлежащего сепарации, оценивается рядом критериев [3]: производственной эффективностью, экономической эффективностью, технологической эффективностью.
При очистке семян от трудноотделимых сорняков более целесообразно брать за критерий, принятую в работе, технологическую эффективность [48]
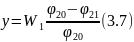
где
 - содержание сорняков в первой фракции,
шт/кг;
- содержание сорняков в первой фракции,
шт/кг;
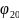 -
содержание сорняков в исходном материале,
шт/кг;
-
содержание сорняков в исходном материале,
шт/кг;
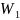 -
выход основного продукта в первую
фракцию в долях единицы.
-
выход основного продукта в первую
фракцию в долях единицы.
Для предсказания направления, в котором величина параметра оптимизации y увеличивается быстрее, чем в любом другом направлении и для описания исследуемой области поверхности отклика требуется математическая модель, под которой подразумевается уравнение, связывающее параметры оптимизации y с входящими факторами Xi.
По результатам предварительных опытов были выбраны шесть факторов, оказывающих основное влияние на процесс очистки на лабораторной экспериментальной установке:
Напряжение, подводимое к решету (U) – X1
Амплитуда колебаний решета (r) – X2
Частота колебаний решета (n) – X3
Продолжительность цикла (tц) – X4
Коэффициент заполнения решета зерном (КЗП) – X5
Относительная длительность подачи напряжения (εн) – X6
Продолжительность цикла определяется выражением

где
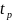 - длительность подачи напряжения, с;
- длительность подачи напряжения, с;
 -
длительность паузы, с.
-
длительность паузы, с.
Относительная длительность подачи напряжения определяется выражением
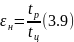
Уровни и интервалы варьирования факторов представлены в таблице 3.1.
Таблица 3.1 – Основные уровни и интервалы варьирования факторов при очистке овса от овсюга на лабораторной установке
Исследуемые факторы |
|
|
|
|
|
|
уровни |
||||||
Верхний (+1) |
26,6 |
2,66 |
430,0 |
3,66 |
0,63 |
0,916 |
Нулевой (0) |
20,0 |
2,00 |
410,0 |
3,00 |
0,50 |
0,750 |
Нижний (-1) |
13,4 |
1,34 |
390,0 |
2,34 |
0,37 |
0,584 |
Интервал варьирования |
6,6 |
0,66 |
19,9 |
0,66 |
0,13 |
0,166 |
Звездные точки |
10,0 |
1,00 |
30,0 |
1,00 |
0,20 |
0,240 |
Нижний уровень факторов , , был взят на основании теоретических исследований.
В лабораторной установке был взят малый диапазон варьирования факторов , , , кроме этого трудно было учесть как фактор скорость движения ленты – решета и количество подаваемого материала.
В опытной полупроизводственной установке все это было учтено и выбраны 6 факторов, оказывающих основное влияние на процесс сепарации:
Напряжение, подводимое к ленте-решету (U) – X1
Амплитуда колебаний ленты-решета (r) – X2
Частота колебаний ленты-решета (n) – X3
Продолжительность цикла (tц) – X4
при εн = 0,5
Скорость движения ленты-решета (VЛ) – X5
Количество подаваемого материала (ПЗ) – X6
Уровни и интервалы варьирования факторов представлены в таблице 3.2.
Таблица 3.2 – Основные уровни и интервалы варьирования факторов при очистке овса от овсюга технологическим блоком опытной полупроиз-водственной установки
Исследуемые факторы |
, кВ |
, мм |
, кол/мин |
, с |
, м/с |
,
кг/с |
уровни |
||||||
Верхний (+1) |
35 |
6 |
430 |
5 |
0,615 |
9,70 |
Нулевой (0) |
25 |
4 |
410 |
4 |
0,504 |
6,95 |
Нижний (-1) |
15 |
2 |
390 |
3 |
0,393 |
4,20 |
Интервал варьирования |
10 |
2 |
20 |
1 |
0,111 |
2,75 |
Звездные точки |
15 |
3 |
30 |
2 |
0,168 |
4,20 |
Функция
отклика y
= f(
,
…
 )
представляется в виде полинома второй
степени [96]
)
представляется в виде полинома второй
степени [96]
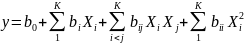 (3.10)
(3.10)
где
 - коэффициенты регрессии, по величине
которых можно судить о степени влияния
соответствующих факторов;
- коэффициенты регрессии, по величине
которых можно судить о степени влияния
соответствующих факторов;
K – число независимых переменных (факторов).
Чтобы оценить все коэффициенты квадратичной модели надо иметь план, в котором каждая переменная варьирует хотя бы на трех разных уровнях. Кроме того, план должен удовлетворять определенному критерию оптимальности. Исходя из практических соображений, следует использовать такие планы, которые требуют наименьших затрат на реализацию эксперимента. Поскольку затраты не эксперимент пропорциональны числу опытов N, естественно выбрать планы, в которых N не сильно превышает число определяемых констант.
Наиболее часто используются центральные композиционные ортогональные и рототабельные планы, разработанные Боксом [24, 25]. Однако, рассчитанные на последовательную стратегию экспериментирования, эти планы требуют все-таки большого количества опытов N, которое значительно превышает число определяемых констант.
В работе использованы планы Хартли, требующие меньшего числа опытов, чем планы Бокса [89]. По Лисенкову А.Н. [67] для планирования шестифакторного эксперимента (число констант равно 28) наименьшее число опытов необходимое по планам Хартли равно 29.
Метод
построения этих планов сводится к
использованию наименьшей возможной
регулярной реплики от полного факторного
эксперимента типа
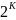 в качестве «ядра» композиционной схемы.
При этом единственное требование,
предъявляемое к этим планам, состоит в
том, чтобы в такой реплике не коррелировали
между собой только двухфакторные
взаимодействия.
в качестве «ядра» композиционной схемы.
При этом единственное требование,
предъявляемое к этим планам, состоит в
том, чтобы в такой реплике не коррелировали
между собой только двухфакторные
взаимодействия.
Другая особенность планов Хартли состоит в том, что повторные опыты ставятся только в дополнительных (звездных) точках. При этом повторные опыты рассматриваются как самостоятельные. В ядре плана тоже могут ставиться повторные опыты, но они не считаются самостоятельными.
Для того, чтобы компенсировать влияние систематических ошибок, причиной которых могли быть случайные колебания напряжения в электросети, температуры и влажности воздуха в помещении, изменение состава сортируемой смеси-опыты рандомизировали по времени, из-за чего порядок опытов в эксперименте принимали случайным (с использованием таблицы случайных чисел).
Постановка
параллельных опытов не дает полностью
совпадающих результатов, так как
существует ошибка опыта. Для этого опыты
повторяли несколько раз и затем брали
среднее арифметическое
 всех n отдельных результатов.
всех n отдельных результатов.
Наличие
отклонения результатов любого опыта
от среднего арифметического свидетельствует
об изменчивости, которую измеряли
дисперсией
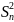 .
.
Для определении грубых ошибок использовали критерии Стьюдента:
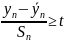 (3.11)
(3.11)
где
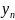 - результат отдельного опыта;
- результат отдельного опыта;
 – среднее
квадратическое отклонение.
– среднее
квадратическое отклонение.
Значение t брали из таблицы t – распределений для принятого уровня значимости (0,05). Опыт считали бракованным, если экспериментальное значение t по модулю было больше табличного. Для вычисления и использовали данные наблюдений без резко отличающихся величин.
Для нахождения дисперсии параметра оптимизации необходимо проверить однородность дисперсии всех отдельных опытов. Однородность дисперсии проверяли с помощью критерия Кохрена [25], представляющего собой отношение максимальной дисперсии к сумме всех дисперсий
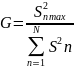 (3.12)
(3.12)
Дисперсии считали однородными, если экспериментальное значение критерия Корхена не превышало табличного.
После получения результатов опыта и расчета дисперсии параметра оптимизации вычисляли коэффициенты регрессии модели.
Для планов Хартли вычисление коррелированных коэффициентов регрессии производили по формулам [24,89]
 (3.13)
(3.13)
 (3.14)
(3.14)
где
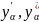 - значения выхода в соответствующих
звездных точках.
- значения выхода в соответствующих
звездных точках.
Звездное плечо α определяли по формуле
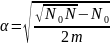 (3.15)
(3.15)
где N – общее число опытов;
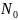 -
число опытов в ядре плана;
-
число опытов в ядре плана;
m – число повторностей.
Некоррелированные коэффициенты определяли соответственно
 (3.16)
(3.16)
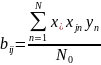 (3.17)
(3.17)
Коэффициенты у квадратичных членов уравнения регрессии определяли по формуле
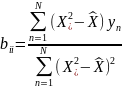 (3.18)
(3.18)
где
 (3.19)
(3.19)
Свободный член уравнения регрессии вычисляется по формуле
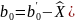 (3.20)
(3.20)
где
 (3.21)
(3.21)
Получив уравнение регрессии проверяли зависимость коэффициентов с помощью построения доверительного интервала.
Выражения для дисперсии коэффициентов регрессии имеют вид
а) для линейных членов
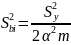 ,
(3.22)
,
(3.22)
где
 (3.23)
(3.23)
б) для парных взаимодействий
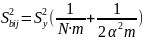 (3.24)
(3.24)
в) для квадратичных членов
 (3.25)
(3.25)
Доверительный интервал
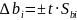 ,
(3.26)
,
(3.26)
где
t – табличное значение критерия Стьюдента
при числе степеней свободы, с которым
определялось
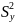 и выбранном уровне значимости;
и выбранном уровне значимости;
 – квадратическая
ошибка коэффициента регрессии.
– квадратическая
ошибка коэффициента регрессии.
Коэффициент считается значимым, если его абсолютная величина превышает значение доверительного интервала.
Исключив из полученного уравнения регрессии незначимые коэффициенты, проверяли адекватности уравнения, то есть способность модели предсказывать результаты эксперимента в некоторой области с требуемой точностью, по формуле [70]
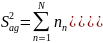 (3.27)
(3.27)
где
 – предсказанное по уравнению значение
параметра оптимизации в n- м опыте;
– предсказанное по уравнению значение
параметра оптимизации в n- м опыте;
f – число степеней свободы для дисперсии адекватности, которое равно числу различных опытов (N), результаты которых используются при подсчете коэффициентов регрессии минус число определяемых коэффициентов, (т.е. f = N-C).
Затем находили F – критерий (критерий Фишера), пользуясь выражением [61]
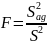 ,
(3.28)
,
(3.28)
который сравнивали с табличными значениями.
Если расчетное значение не превышало табличного, то с соответствующей доверительной вероятностью модель считали адекватной.
С целью поиска максимального значения параметра оптимизации y в исследованной области проводили предварительный анализ уравнения регрессии. После анализа коэффициентов при параметрах, некоторые параметры фиксировали на краю исследуемой области и искали значения остальных, подставляя принятые значения зафиксированных параметров. Затем, приравняв к нулю частные производные по остальным параметрам, получали системы уравнений, решение которых позволило найти параметры, обеспечивающие наибольший y в исследованной области.
Используя действительные значения полученных параметров, проводили проверочный технологический эксперимент с двадцатикратной повторностью.

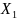 ,
кВ
,
кВ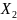 ,
мм
,
мм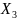 ,
кол/мин
,
кол/мин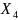 ,
с
,
с ,
,
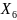 ,
,