1.4. Анализ теоретических положений поведения вытянутых частиц на плоскости в электростатическом поле

Из анализа вышеприведенных методов очистки овса от овсюга с использованием электрического поля наибольший интерес представляет применение электростатического поля с использованием плоских поверхностей (решет, лент), колеблющихся или движущихся продольно.

Поведение вытянутых частиц в электростатическом поле на плоскости впервые было подробно рассмотрено Шмигелем В.Н. [93]. Энергия электростатического поля играет ту же роль в электростатике, что и потенциальная энергия в механике. При помещении в это поле частиц с относительной диэлектрической проницаемостью ε>1 энергия поля уменьшается. Если же частица имеет вытянутую форму, то уменьшение энергии будет зависеть от ориентации частицы. Наибольшим оно будет при ориентации частицы длинной осью вдоль силовых линий поля. Так как поле постоянно стремится уменьшить свою энергию, оно создает вращающий момент поля М_З, ориентирующий частицу.

Автор [93] рассмотрел действующие на частицу силы и моменты сил и получил аналитические зависимости. Была дана графическая интерпретация полученных зависимостей, пропорциональных действующим моментам в зависимости от угла γ наклона большей оси частицы к плоскости электродов, образовавших поле.

Впервые было рассмотрено условие ориентировки вытянутых частиц на плоскости электрода в электростатическом поле, введено понятие моментов, содействующего и противодействующего ориентировке частицы.

Зерно принималось за диэлектрическую эллипсоидальную частицу, форма которой определялась коэффициентом сферичности [40] (отношение меньшей оси эллипсоида вращения «b» к большей «α»). Ее ориентировка на наклонной под углом β к горизонту плоскости осуществляется в основном вращающим моментом электростатического поля [94].

, (1.1)

где Е - потребная для ориентировки напряженность внешнего электроста-тического поля;

ε_о - электрическая постоянная;

- объем эллипсоидальной частицы;

- функция, характеризующая влияние формы и относительной диэлектрической проницаемости на вращающий момент поля.

Содействует ориентировке частицы и содействующий момент , составляющей силы тяжести F_Т = mg вдоль плоскости электрода.

(1.2.)

Противодействующий момент составляющей силы тяжести, нормальной к электроду, препятствует ориентировке частиц

(1.3.)

В этих выражениях:

(1.4.)

(1.5.)

- коэффициент симметрии центра тяжести [93,94]

где λ – кратчайшее расстояние от конца зерновки до центра тяжести частиц.

На рис. 1.8. представлена схема действующих на эллипсоидальную частицу сил и моментов при расположении частицы на наклонном электроде в электростатическом поле.

Расстояние от геометрического центра до точки R касания частицы с плоскостью имеет определенное выражение:

. (1.6.)

Рисунок 1.8 – Схема сил и моментов, действующих на эллипсоидальную частицу при расположении в электростатическом поле на наклонном электроде.

Так как диэлектрическая частица, находящаяся на электроде в электростатическом поле способна получить заряд [10], то появляется электрическая сила и момент её, дополнительно содействующий ориентировке частицы при меньших напряженностях поля.

Басов А.М. и Шмигель В.Н. [10] рассматривали задачу из условия, что заряд находится в центре тяжести зерна и сила зеркального отображения направлена к плоскости верхнего электрода системы электродов образовавших поле (рисунок 1.8).

Условие ориентировки заряженной эллипсоидальной частицы со смещенным центром тяжести на наклонной под углом β неподвижной плоскости записывалось выражением [93]

, (1.7.)

где - сумма содействующего и противодействующего ориентировке частицы моментов;

– коэффициент влияния заряда.

В исследованиях Шмигеля В.Н. [93] впервые упоминается о начальном угле наклона γ_о большей оси частицы к плоскости электродов. Автор указывает, что этот угол может быть обусловлен начальной ориентировкой частицы в электростатическом поле, когда М_Э=М_FТ или подпиранием поверхности частицы другими лежащими на плоскости частицами. Исследования [93], проведенные с использованием киносъемки показали наличие этого угла, имеющего величину 25^о.

В последующих исследованиях других авторов [19] дается зависимость изменения угла γ поворота семян от времени их подъема в электростатическом поле с учетом того, что частицы имеют при помещении их в поле начальный угол γ ^о. К сожалению, не ясно относится ли эти значения к среднему результату по массе семян или к одному зерну.

Однако, как показали экспериментальные исследования Завяцкаса В.К. [37], и без наличия поля длинная ось частицы, ввиду смещения центра тяжести относительно геометрического центра и некоторого отличия формы семян от эллипсоида вращения, составляет определенный угол с плоскостью, на которой она расположена. Этот угол исследователь называл углом поворота и, основываясь на своих теоретических исследованиях, указал, что угол имеет важное значение для ориентировки частиц.

Теоретических же исследований по определению начального угла наклона частицы при отсутствии поля ни один из исследователей не проводил.

В работе Шмигеля В.Н. [98] приведены обоснования на базе известных положений получения повышенной напряженности перераспределенного с помощью диэлектрического слоя электростатического поля при очистке семенных смесей с вытянутыми частицами [98,18]

. (1.8.)

Здесь напряженность в воздушном промежутке;

U – напряжение на электрода;

h_В, h_СЛ – соответственно высота воздушного промежутка и диэлектрического слоя;

γ_В, γ_СЛ – проводимость воздушного промежутка и диэлектрического слоя.

Здесь же автор [98] приводит выражение максимальной относительной скорости движения частицы, необходимой для прохода частицы с размерами «а» и «b» в отверстие диаметра D наклоненного к горизонту под углом β продольно колеблющегося решета.

(1.9.)

Однако задача решалась без учета смещения центра тяжести частицы и влияния электрических сил поля [94].

Шмигель В.Н. [98] не рассматривал относительного перемещения вытянутой частицы по решету и влияния его на кинематику колеблющейся системы.

В 1972 г. были опубликованы исследования Будзко А.И., Бородина И.Ф. и Тарушкина В.И. [20] и создан электростатический классификатор семян [17] с боковым наклоном электрода.

При рассмотрении поведения частиц и их ориентировки на плоскости в электростатическом поле предполагали, что вращающему моменту поля М_Э противодействует только момент силы тяжести. Такой вывод справедлив только в случае, если на частице отсутствует свободный заряд [37]. Однако из прежних исследований известно [10], что в результате контакта с электродом диэлектрическая частица приобретает свободный заряд.

Впервые время ориентировки вытянутых частиц, находящихся в электростатическом поле на плоскости и отрывающихся от неё, было определено аналитически и проверено экспериментально Шмигелем В.Н. [96], а затем более глубоко аналитически исследовано Агрономовой В.А[1].

Позднее в исследованиях Будзко И.А., Бородина И.Ф., Тарушкина В.И. [19] были приведены экспериментальные результаты времени ориентации частиц, также отрывающихся от плоскости в электростатическом поле. По данным расшифровки кинограмм авторы записали время ориентировки частиц t_о как

t_о= t_З + t_П (1.10.)

где t_З - время, в течение которого частица приобретает заряд на плоскости, необходимый для ее подъема;

t_П= время подъема частицы.

Таким образом, никто из упомянутых исследователей не определил время ориентации частицы без отрыва от плоскости в зависимости от различных параметров частиц и поля.

Завяцкас В.К. [37] развил теоретические обоснования условий ориентировки диэлектрических и проводящих частиц, получивших контактный заряд в электростатическом поле на горизонтальной плоскости.

Опираясь на работы ряда исследователей [77,117], Завяцкас В.К. указывает, что при контактной зарядке свободные электроны стекают с электрода на частицу, если она лежит на электроде отрицательной полярности. При этом нижняя сторона частицы, на которой имеются связанные положительные заряды, как бы нейтрализуются.

На частице остается только отрицательный заряд, который сконцентрирован в верхней ее половине. Поэтому центр заряда не совпадает с геометрическим центром частицы.

Считая, что все наведенные и свободные заряды сосредоточены непосредственно у поверхности эллипсоидальной частицы, принимают [45], что смещение заряда вверх от геометрического центра будет на , где b – малая ось частицы. Таким образом, в точке К (рисунок 1.9) на частицу по нормали к электроду действуют [37] сила взаимодействия поля с заряженной частицей

F₁ = Q · Е (1.11.)

и сила зеркального отображения

. (1.12.)

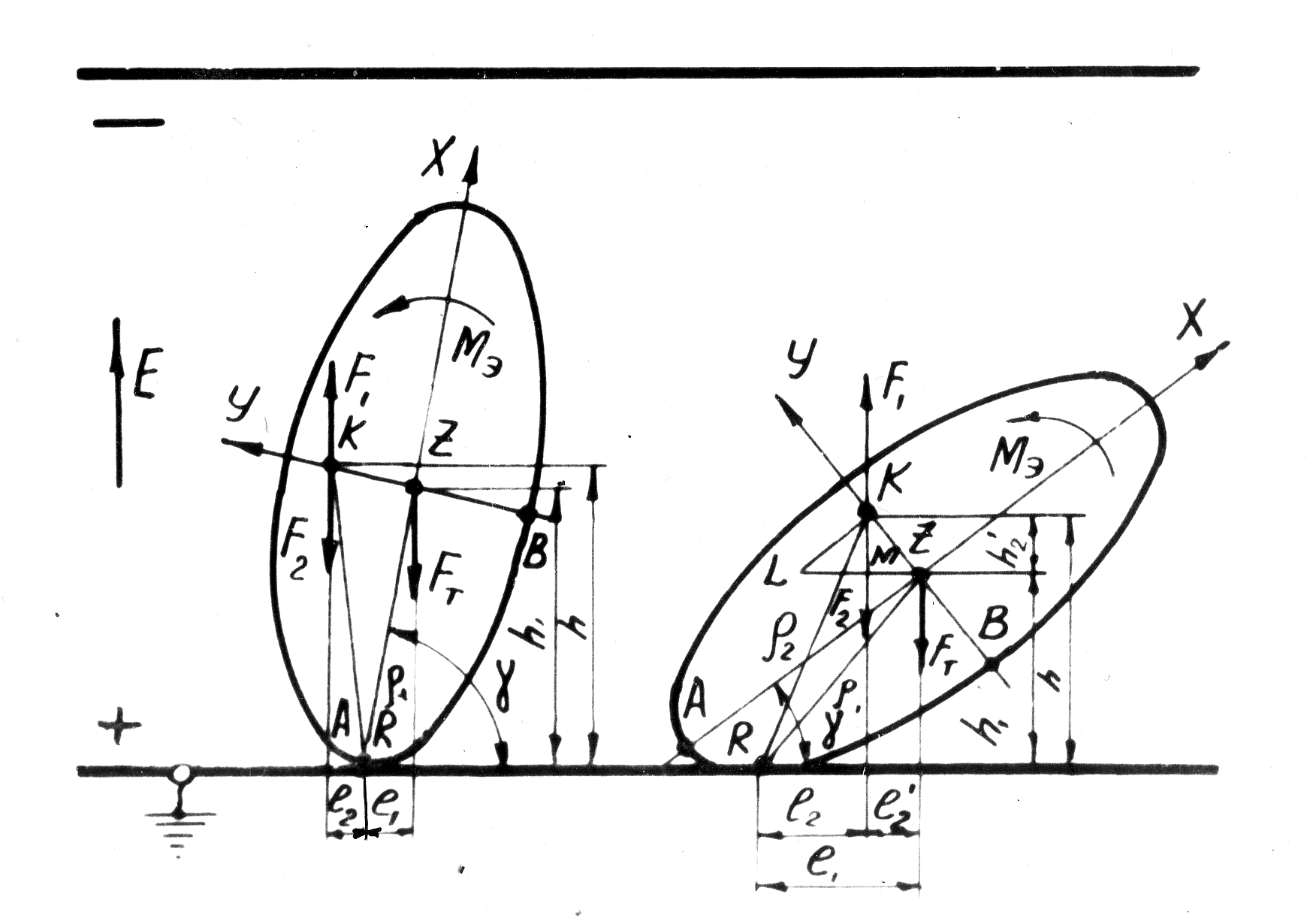
Рисунок 1.9 – Схема сил и моментов, действующих на заряженную диэлектрическую эллипсоидальную частицу при расположении ее в электростатическом поле горизонтальном электроде

где ε_С – диэлектрическая проницаемость среды (для воздуха ε_С = 1);

h – расстояние от центра заряда до плоскости.

Соответственно силам на частицу действуют содействующий М_F1 и противодействующий М_F2 ориентировке частицы моменты сил

М_F1 = F₁ · l₂ (1.13)

и

М_F2 = F₂ · l₂ , (1.14)

причем

l₂ = l₁ – l₂^' = αК^'м - , (1.15)

h = h₁ – l₂^' = αК^"м+ , (1.16)

где и взяты из уравнений (1.5) и (1.4).

После ряда преобразований полученных выражений (1.13) и (1.14) Завяцкас В.К. приводит зависимости для моментов сил М_F1 и М_F2 в следующей записи:

М_F1 = Q·Е·α·К₁, (1.17)

где (1.18)

и

, (1.19)

где

(1.20)

Условие ориентировки частицы Завяцкасом В.К. было представлено следующим выражением [37]

М_Э + М_F1 М_FТ + М_F2 + М_С (1.21)

Причем величина предельного свободного заряда, определяющего силы F₁ и F₂, при размещении эллипсоидальной частицы длинной осью поперек поля (начало ориентирования), согласно [64,68] имеет вид:

, (1.22)

Решение уравнения (1.21.) после подстановок всех величин позволило Завяцкасу В.К. [37] определить напряженность начала ориентировки, которая принята им за признак разделения

. (1.23)

Здесь диэлектрический коэффициент формы Завяцкасом В.К. представлен в качестве безразмерной величины.

В развернутом виде дает зависимость между различными безразмерными физическими параметрами ориентируемой заряженной частицы

, (1.24)

где – коэффициент, характеризующий изменение момента силы тяжести в зависимости от формы частицы и угла γ с учетом асимметрии центра тяжести частицы;

– коэффициент осевой деполяризации при ориентации частицы длинной осью поперек силовых линий поля.

Анализ изменения К_дф в функции р при различных К показал, что с увеличением коэффициента симметрии и уменьшением коэффициента сферичности К_дф возрастает. Изменение К_дф в функции γ при разных р и ε частицы имеет более сложную зависимость, представленную на рисунке 1.10 (для постоянного К = 0,2). В действительности К_дф по Завяцкасу В.К. [37,38] должен зависеть от .

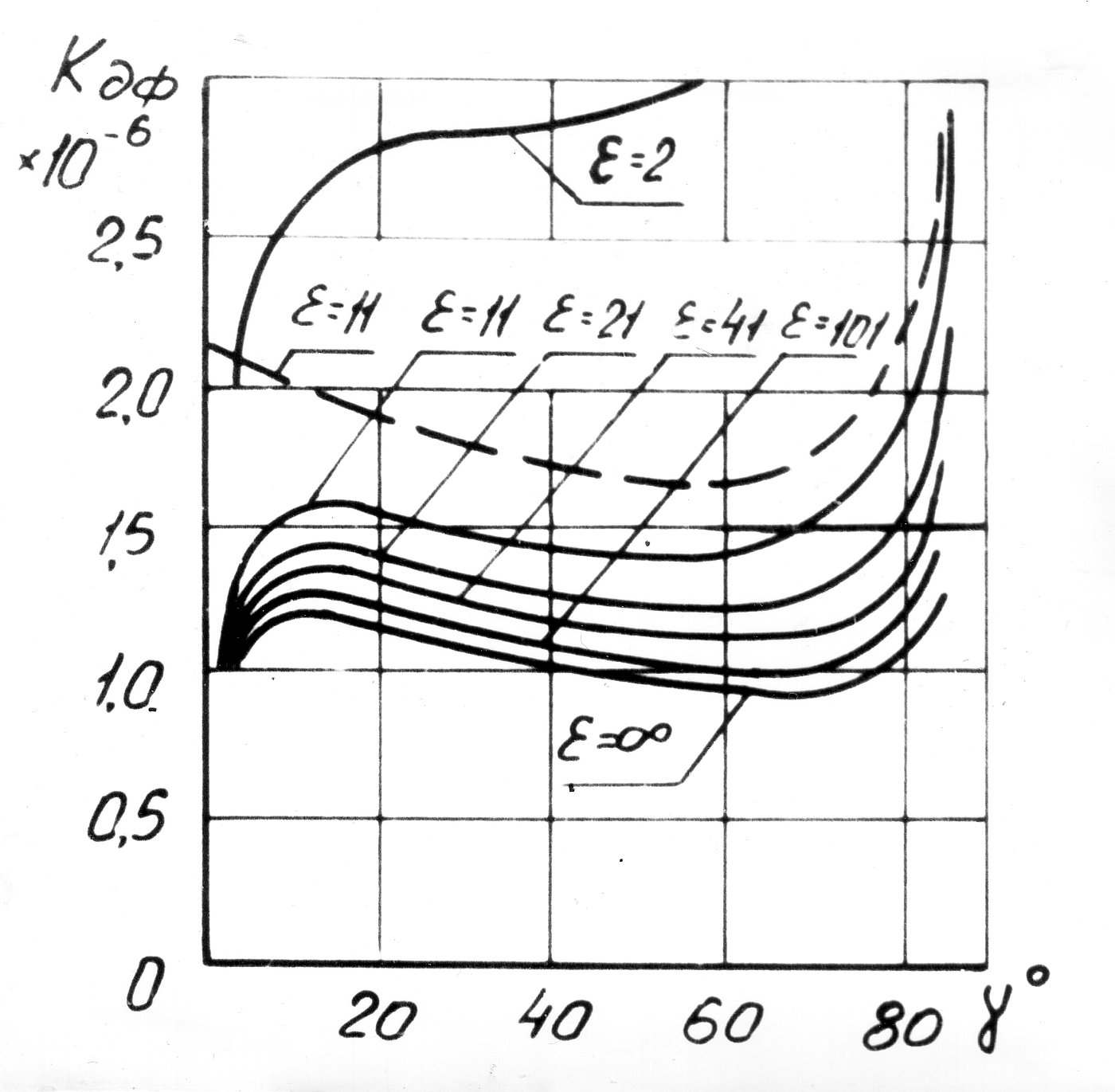
Рисунок 1.10 – Изменение К_ДФ в функции γ при различных р и Е

(для постоянного К = 0,2)

Динамику процесса ориентировки при совокупном воздействии на частицу вращающего момента поля М_Э, момента силы взаимодействия поля и заряженной частицы М_F1, момента силы тяжести М_FТ и момента силы взаимодействия заряженной частицы с плоскостью М_F2 можно расписать уравнением

М_Э + М_F1 - М_FТ - М_F2 = J^'τ , (1.25)

где J^' – момент инерции частицы относительно оси, проходящей через точку R касания частицы и плоскости электрода;

τ – угловое ускорение в процессе поворота частицы.

Однако исследователь [64] принял механический момент инерции по формуле, использованной Агрономовой В.А. [1] при свободном полете частицы и повороте ее относительно центра тяжести.

J^' = 0,05m (α² + в²) (1.26)

Поэтому в записанном им дифференциальном уравнении [37]

(1.27)

необходимо уточнить правую часть, так как:

– во-первых, частица поворачивается не относительно центра тяжести, а относительно точки касания частицы с плоскостью;

– во-вторых, механический момент инерции будет изменяться в процессе ориентировки.

В связи с этим требуют исправления и результаты решения управления (1.26) полученные на ЭЦВМ. Графики иллюстрирующие это решение [37] показывают (рисунок 1.11), что частица, находящаяся на электроде длительное время (0,5 секунд и более), совершает в сориентированном состоянии колебания в пределах углов 45^о γ 135^о в начале с постепенным снижением амплитуды колебаний через некоторое время. Однако, как показала проведенная нами скоростная фотосъемка, такое решение не отражает действительного процесса.

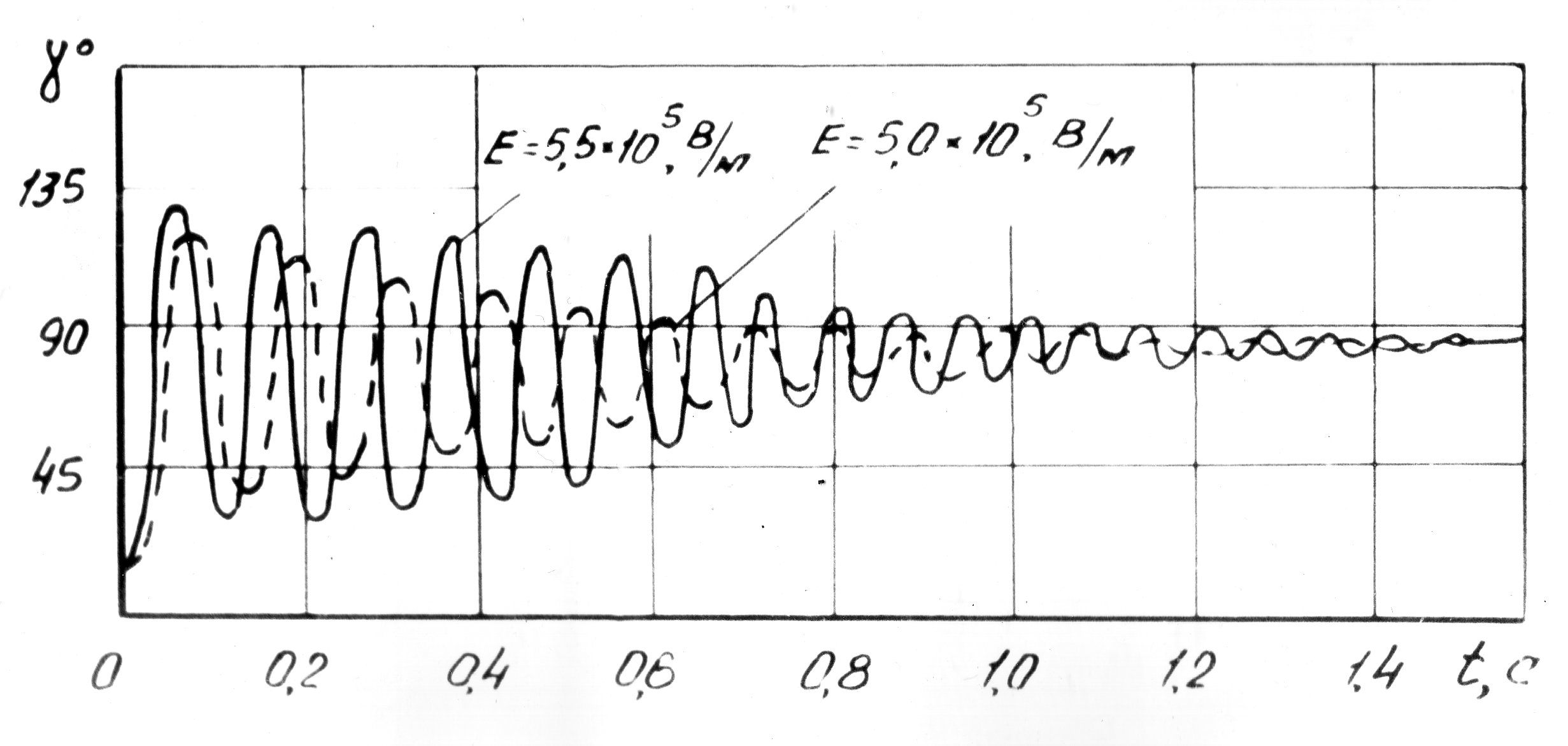
Рисунок 1.11 – Изменение угла γ наклона частиц малой проводимости в функции времени t при ориентировке их в электростатическом поле на горизонтальном электроде (α = 14·10^-3 м, К = 0,3, m = 30·10^-6 кг., ε = 41, р = 0,8, γ_о = 10^о)

Надо отметить, что при решении дифференциального уравнения автор работы [37] учитывал, что частицы имеют начальный угол наклона γ_о, однако он не придал значения тому факту, что начальные углы γ_о для различных частиц различны. Им было принято, что γ_о величина постоянная для всех семян.

Кроме того, значение γ_о исследователь [37] принял необоснованно завышенным (≈10^о).

Все отмеченные выше недостатки известных исследований говорят о том, что процесс ориентировки вытянутых частиц на неподвижной и подвижной горизонтальных плоскостях необходимо дальше и более детально исследовать с учетом действующих на частицы сил и моментов.

С другой стороны, необходимо вести дальнейшую разработку способов и устройств, которые могли бы обеспечить более качественную очистку семян овса от овсюга.