2.2 Проверка на нагрев методом средних потерь.

Температура нагрева двигателя не превышает допустимую величину при условии:

, (9)

где ΔР_НОМ = Р_2НОМ (1-η_НОМ)/ η_НОМ, ΔР_СР – номинальные и средние потери

электродвигателя, Вт.

Коэффициент тепловой перегрузки К_Т определяется по формуле:

, (10)

где Т_н – постоянная времени нагрева проверяемого двигателя, мин;

, (11)

где m – масса двигателя, кг; τ_доп – предельно–допустимое превышение температуры нагрева обмоток двигателя, ^◦С. Для двигателей с высотой оси вращения 50…132 мм применяется класс В (τ_доп=80^◦С), 160…355 мм – класс F (τ_доп=100^◦С). Высота оси вращения указывается в типоразмере двигателя. Например, 4А100S4У3 имеет высоту оси 100 мм.

Определим потери мощности двигателя на каждом периоде нагрузки:

(12)

Значение Р_i берутся из нагрузочной диаграммы (Р₁ – Р₄). Коэффициент полезного действия η_i при любой нагрузке определяется:

(13)

где х_i показатель загрузки двигателя на i-ом интервале нагрузочной диаграммы.

(14)

Расчёт упрощается, если воспользоваться данными (приложение 2) и построить график изменения КПД и cos φ двигателя от нагрузки на валу (рис. 2). В этом случае по оси ординат откладывается показатель х_i.

Рис. 2. – График изменения КПД и cos φ двигателей серии 4А

от нагрузки на валу

Величина средних потерь в двигателе за время работы:

, (15)

Если выполняется условие (9), то при заданной нагрузке температура двигателя не превысит допустимую величину. Если же это условие не выполняется нужно выбрать двигатель на одну ступень выше и повторить проверку на нагрев.

2.3 Проверка на нагрев методом расчета температуры

В расчётах температуры нагрева двигателя τ определяют не действительное её значение, а превышение над температурой окружающей среды.

Значение температуры превышения τ в любой момент времени определяется по выражению:

, (16)

где τ_устi – установившееся значение температуры превышения на участке диаграммы, град.

Установившееся значение температуры превышения на каждом интервале нагрузки:

. (17)

Теплоотдача А, Вт/град:

, (18)

Начальное значение температуры превышения принимается равным 0, а далее конечное значение температуры превышения на первом интервале равное начальному на втором и т.д.

Расчет температуры превышения на первом участке (0…t₁) через t₁/2 и t₁ минут:

, (19)

, (20)

На втором участке: τ_2нач= τ_1кон

, (21)

, (22)

На третьем и четвёртом участке расчёт производится аналогично.

Кривая охлаждения двигателя:

, (23)

где Т₀ – постоянная времени охлаждения двигателя, мин;

τ_нач – начальная температура охлаждения двигателя после его отключения, принимается равной τ_4кон, ^◦С. Т₀=2∙ Т_н.

Принимаем t= Т₀, 2Т₀, 3Т₀, 4Т₀, 5Т₀.

Результаты расчетов сводим в таблицу № 2 и 3.

Таблица №2 – Данные расчетов нагрева двигателя

Нагрев	Р1			Р2		Р3		Р4
Расчетная точка	0	0,5t1	t1	0,5t2	t2	0,5t3	t3	0,5t4	t4
Время, мин	0
Темп-ра, ◦С	0

Таблица №3 – Данные расчетов охлаждения двигателя

Расчетная точка	0	Т0	2Т0	3Т0	4Т0	5Т0
Время, мин
Темп-ра, ◦С

По результатам расчета нагрева и охлаждения двигателя строим график рис. 3.

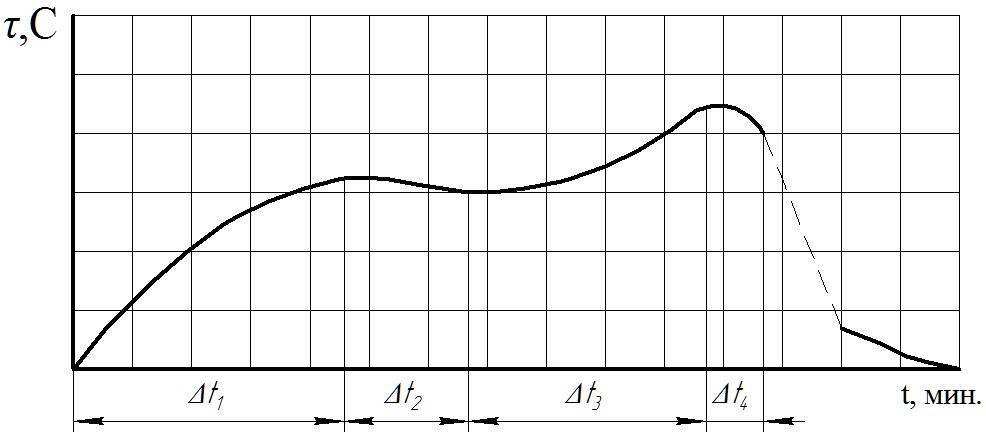
Рис. 3 – График изменения температуры электродвигателя

Анализирую график рис. 3, делаем вывод о превышении или не превышении электродвигателем допустимой величины температуры в процессе работы и, как правило, о прохождении двигателя по нагреву или нет.

2.4 Проверка выбранного двигателя на нагрев методом эквивалентных величин.

2.4.1 По паспортным данным двигателя строим нагрузочную диаграмму при пуске.

По заданию пуск осуществляют с постоянным моментом сопротивления, равным 0,3М_Н. Момент инерции рабочей машины равен 2J_д.

Каждая точка механической характеристики имеет две координаты: угловая скорость ω и момент, развиваемый электродвигателем, М.

Точка 1: координаты - ω_о, М₀=0.

, (24)

где ω_о – угловая синхронная скорость, рад/с;

n₀ – синхронная скорость, об/мин (таблица №1).

Точка 2: координаты – ω_Н, М_Н.

, (25)

, (26)

где ω_Н – угловая номинальная скорость, рад/с;

S_Н = (n₀ – n)/n₀ – номинальное скольжение;

М_Н – номинальный момент, Н∙м;

Р_Н – номинальная мощность двигателя, Вт (таблица №1).

Точка 3: координаты – ω_К, М_К.

, (27)

, (28)

где ω_К – угловая скорость, соответствующая критическому моменту, рад/с;

– критическое скольжение;

М_К – критический момент, Н∙м;

m_К – кратность критического момента (таблица №1).

Точка 4: координаты – ω_М, М_М.

, (29)

, (30)

где ω_М - угловая скорость, соответствующая минимальному моменту, рад/с;

S_М – минимальное скольжение, S_М =0,85…0,87;

М_М – минимальный момент, Н∙м;

m_М – кратность минимального момента (таблица №1).

Точка 5: координаты – ω_П=0, М_П.

, (31)

где М_П – пусковой момент, Н∙м;

m_П – кратность пускового момента (таблица №1).

Электромеханическая характеристика.

Точка 1: имеет координаты – ω₀, I₀.

, (32)

, (33)

, (34)

где I_о – ток на холостом ходу, А;

I_Н – номинальный ток, А;

U_Н = 380 – номинальное напряжение, В;

η_Н – КПД при номинальной скорости (таблица №1);

cosφ_Н – коэффициент мощности при номинальной скорости (таблица №1).

Значение скоростей ω₀, ω_Н, ω_К берём из предыдущих расчётов механической характеристики электродвигателя по пяти точкам.

Точка 2: имеет координаты – ω_Н, I_Н (формула 33).

Точка 3: имеет координаты – ω_К, I_К.

, (35)

, (36)

где I_П – пусковой ток, А;

I_К –ток при критическом моменте, А;

i_П – кратность пускового тока (таблица №1).

Точка 4: имеет координаты – ω_П=0, I_П (формула 36).

По этим данным во втором квадранте системы координат, необходимо построить механическую М(ω), электромеханическую I(ω) характеристики электродвигателя и механическую характеристику рабочей машины М_C(ω) и определить установившуюся скорость ω_у (точку пересечения механических характеристик электродвигателя и рабочей машины) (рис. 4).

Отрезок оси от 0 до ω_у, необходимо разделить на 6 отрезков 0-1; 1-2; 2-3 и т.д. Через точки 1, 2, 3 и т.д. проводим прямые, параллельные оси моментов и времени. Для каждой скорости ω₁, ω₂, ω₃ … по графикам М_Д(ω) определить значения моментов двигателя М_П, M₁₁, М₁₂... и внести их в таблицу 4.

Рассчитать динамический момент системы М_ДИНi = М_Дi - М_С для каждого i значения скорости. Допустим для ω₂: М₄₂ = М₁₂ - М_С = М₁₂ – 0,3М_Н. По данным расчетов построить график М_ДИНi(ω). Операция определения М_ДИН часто выполняется графическим способом. Так, на рисунке для каждого значения скорости, допустим ω₃ замеряется отрезок 3-13, равный моменту двигателя М₁₃ из него вычитается отрезок 3-23 момента М_C. Динамический момент на скорости ω₃ равен М₄₃. Отрезки 3-23 и 43-13 равны.

Таблица №4 – Результаты расчетов нагрузочных диаграмм при пуске двигателя и рабочей машины

Точка i			0	1	2	3	4	5	6
1	скорость ωi	рад/с	0	ω1	ω2	ω3	ω4	ω5	ω6
2	∆ ωi	рад/с	0	∆ ω1	∆ ω2	∆ ω3	∆ ω4	∆ ω5	∆ ω6
3	МДi	Нм	MП п	М11	М12	М13	М14	М15	М16
4	МCi	Нм	0,3МН	0,3МН	0,3МН	0,3МН	0,3МН	0,3МН	0,3МН
5	МДИН.i	Нм	МНО но	М41	М42	М43	М44	М45	М46
6	МДИН.СР	Нм	0	М90	М91	М92	М93	М94	М95
7	∆ti	с	0	∆ t1	∆ t2	∆ t3	∆ t4	∆ t5	∆ t6
8	Ii I	А	IП п	I31	I32	I33	I34	I35	I36
9	ti	с	0	t1	t2	t3	t4	t5	t6

Рис. 4 – Графоаналитический метод построения нагрузочных диаграмм

Обратите внимание. При определении динамического момента очень часто в расчеты могут не попасть M_М и М_K, поэтому необходимо специально проверить и достроить динамические моменты при ω_K и ω_М графическим способом.

Меняющийся динамический момент системы на каждом участке скорости заменяем постоянным - средним. Например, на участке 4-5 переменный динамически момент между точками 44 и 45 заменяем постоянным М_ДИН.СР4. Правило замены - косоугольная трапеция, образованная точками 4-44-45-5 заменяется равной ей по площади прямоугольной. Обычно площади этих четырехугольников не определяют, а сравнивают между собой площади отсекаемых треугольников или других сложных фигур (заштрихованных в данном случае). Если рассматриваемый участок близок к прямой линии, как например 42-43, то М_ДИН.СР = 0,5(М₄₃+ М₄₂). Результаты расчетов заносим в таблицу.

Некоторые пояснения к этой таблице. Значения приращения скорости во второй строке определяется как разность между двумя соседними участками скорости ω_i и ω_i-1. Например, если i = 2, то ∆ ω₂ =ω₂ - ω₁.

Время изменения скорости двигателя на Δω:

(37)

Суммарный момент инерции J_Σ = J_ДВ + J_РМ = J_ДВ + 2 J_ДВ = 3 J_ДВ.

Суммарное время разгона электродвигателя определяем по формуле:

(38)

2.4.2 Эквивалентный ток за время пуска:

(39)

I_СР – среднее значение тока двигателя на интервалах времени Δt₁…Δt₆.

2.4.3 Нагрузочная диаграмма двигателя за время работы.

Ток двигателя по интервалам:

, (40)

Величины η и cosφ определяем из пункта 2.2.

С учетом полученных результатов строим нагрузочную диаграмму (рис. 5).

Эквивалентный ток двигателя за время работы:

, (41)

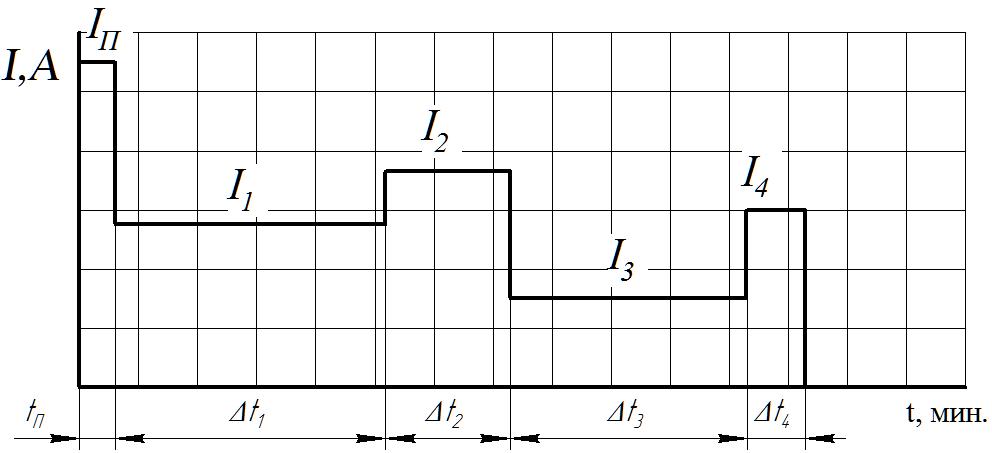
Рис. 5 – Нагрузочная диаграмма электродвигателя

Коэффициент механической перегрузки:

, (42)

Проверяем на нагрев:

, (43)

Если условие (43) выполняется, то расчёт выполнен верно. В противном случае мощность двигателя увеличивается на ступень и расчёт повторяется.