Вопросы для самопроверки к теме 3.1

1. В чём проявляется основное различие между жидкостями и газами?

2. Пригодно ли уравнение Менделеева – Клапейрона для газов любого химического состава?

3. Чем отличается ламинарное течение от турбулентного?

4. Какой критерий предопределяет характер течения при данных условиях?

5. Как определяется гидравлический диаметр канала, по которому движутся газ или жидкость?

0. Тема 3.2. Основные явления

1. В потоках жидкостей и газов

3. Законы сохранения применительно к потокам газов и жидкостей. Фундаментальные законы механики твердого тела сохраняют свое действие и в механике газов и жидкостей. Пусть поток жидкости или газа движется по некоторому каналу (рис. 3.3) в направлении, показанном стрелкой.

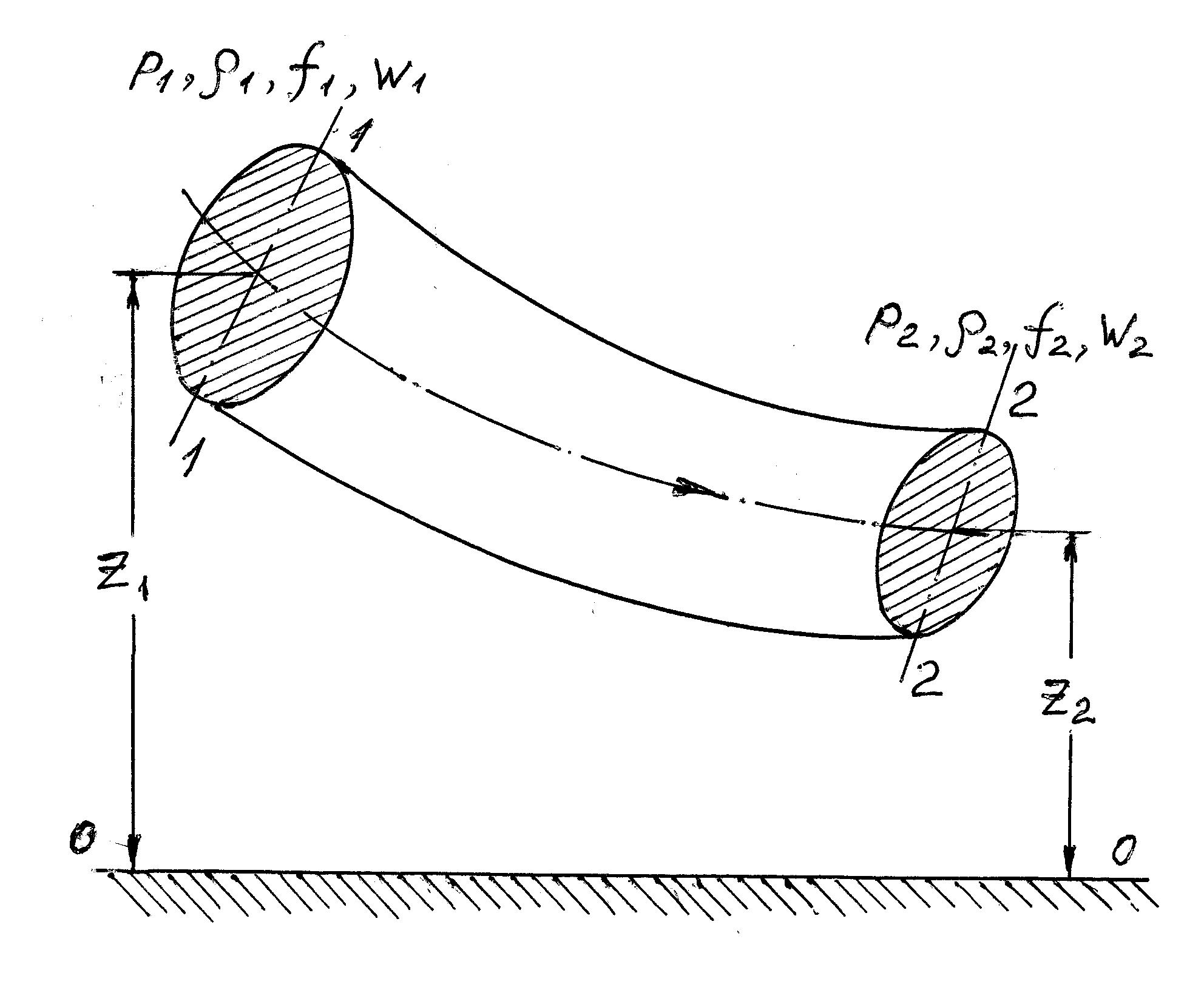
Рис. 3.3. Иллюстрация к законам сохранения массы и энергии

в потоке жидкости или газа

Поток последовательно пересекает сечения 1 - 1 и 2 - 2 со следующими параметрами.

Первое по ходу потока сечение:

- абсолютное давление текущей среды P₁, Па;

- плотность , кг/м³;

- площадь сечения f₁, м²;

- средняя по сечению скорость потока W₁, м/с.

Второе сечение характеризуется аналогичными параметрами, отмеченными подстрочными индексами 2.

Массовые расходы среды в рассматриваемых сечениях, кг/с,

Если поток неразрывен, то есть отсутствуют как потеря текущей среды, так и его приток извне между рассматриваемыми сечениями, то на основании закона сохранения массы

что называют уравнением неразрывности течения.

При равенстве плотностей среды в соответствующих сечениях получаем уравнения объемных расходов, м³/м,

которые при условии неразрывности потока дают

или

^.

Точно так же для потоков жидкости и газа справедлив закон сохранения энергии, который для установившегося течения представлен уравнением Бернулли, для идеальной (лишенной вязкости) среды имеющим вид

где, в дополнение к данным рис. 3.3, z₁ и z₂ – высоты центров тяжести сечений 1-1 и 2-2 относительно некоторой горизонтальной поверхности 0-0; g = 9, 81 – ускорение силы тяжести, м/с².

В последнем уравнении первые два члена каждой части выражают потенциальную энергию одного кубического метра протекающей среды, Дж/м³, согласно элементарному анализу размерностей. При этом первый член выражает потенциальную энергию положения, подобно телу, обладающему силой тяжести G, Н / м³, поднятому на высоту Z, м. Второй член p, Па = Н / м² – представляет собой потенциальную энергию сжатия, подобно энергии сжатой пружины. Последний член является кинетической энергией также одного м³, движущегося в канале или жидкости, Дж / м³.

Таким образом, суммарный запас механической энергии каждого кубического метра идеальных газа или жидкости при движении остается постоянным. При наличии вязкости (неидеальные среды) часть начального запаса механической энергии на пути между сечениями 1-1 и 2-2 теряется на преодоление сил внутреннего трения. В результате эта часть механической энергии превращается в теплоту, которая рассеивается в окружающую среду.

Поэтому запас механической энергии в сечении 2-2 оказывается меньше, чем в сечении 1-1. Как следствие этого, уравнение Бернулли (при не слишком резком изменении сечения канала) приобретает вид

или для несжимаемых сред (ρ = const)

^,

где ∆p – соответствующая потеря энергии.

Говоря о размерности отдельных членов уравнения Бернулли, можно придать им иной смысл. Выше эта размерность представлялась в виде

то есть мы формально получаем размерность давления, или напора. Отсюда члены уравнения Бернулли в инженерной практике называют: – геометрический напор,

Р_ст = Р – статический напор,

– динамический, или скоростной напор,

∆р – потеря напора.

Непосредственному измерению доступны статический и динамический напоры (давления) – рис. 3.4, в то время как геометрический напор может быть только рассчитан по приведенным выше формулам.

Для непосредственного измерения статического и динамического напоров в трубопровод 1 вводят напорную трубку 2. Открытый навстречу потоку конец напорной трубки воспринимает полный напор, равный сумме статического Р_СТ и динамического напоров. Другой конец напорной трубки направлен перпендикулярно потоку и поэтому воспринимает статический напор Р_СТ.

Рис. 3.4. Схема измерения давлений с помощью напорной трубки

Для определения разности полного и статического напоров, то есть динамического напора, напорная трубка подключена к дифференциальному манометру, заполненному рабочей жидкостью, например водой. Разность высот жидкости в коленах дифференциального манометра является мерой динамического напора, поскольку сила тяжести рабочей жидкости высотой h, м, уравновешивает действие измеряемого напора

,

где – плотность жидкости в дифференциальном манометре, кг / м³.

Если же увеличивать скорость потока воздуха, то ламинарное течение при определенных условиях переходит в турбулентное. При этом движение элементарных объемов потока (турбулентных молей) становится хаотическим, струйка дыма практически мгновенно распадается и становится видно, что отдельные частицы или струйки потока движутся не только вперед, но и поперек потока, вещество в котором интенсивно перемешивается.

^,

Напоры обратимы. Так, при расширении канала скорость потока уменьшается, а статическое давление возрастает, и наоборот. Геометрический напор может обращаться в статический на вертикальных участках каналов, где горячие продукты сгорания топлива, более легкие, чем окружающий воздух, создают статическиий напор

где z – высота вертикального участка. Именно поэтому часто наблюдают повышающееся с высотой рабочего пространства печей давление печных газов, выбивающихся в атмосферу через различные неплотности в кладке и арматуре печи.

Потери напора

Различают три основных вида потерь напора потоков жидкостей и газов.

1. Потери при внезапном расширении поперечного сечения канала (рис. 3.5) с уменьшением скорости потока от W₁ в сечении 1–1 (перед расширением) до W₂ (в расширенной части канала, то есть в сечении 2–2.).

Согласно известной теореме Борда и Карно, «потеря напора равна кинетической энергии потерянной скорости»:

Рис. 3.5. Схема внезапного расширения потока от сечения 1–1 к сечению 2–2

^.

2. Потери на местных сопротивлениях. К числу местных сопротивлений относят случаи резкого поворота потока, обтекание потоком встречающихся на его пути тел различной формы, решеток и проч. В этом случае потеря напора

^,

где К_М – коэффициент местного сопротивления, практически не зависящий от числа Рейнольдса и целиком определяющийся геометрическими формами местного сопротивления.

3. Потери на преодоление трения. Учитываются на всем протяжении печных каналов и рассчитываются по формуле Дарси

^,

где L – длина канала, м;

– гидравлический диаметр канала, м;

- коэффициент потерь напора на трение. Для случая ламинарного течения в круглых каналах

^.

При турбулентном течении

^,

где А = 0,32; n = 0,25 – для гладких металлических каналов;

А = 0,175; n = 0,12 – для кирпичных каналов.

Правило Лукашевича и Грум-Гржимайло. Для равномерного распределения газового потока по ряду параллельных вертикальных каналов остывающий газ необходимо направлять сверху вниз, а нагревающий – снизу вверх (рис. 3.6).

Рис. 3.6. К пояснению правила распределения потоков

Если остывающие газы направлять снизу вверх, то при случайном возрастании расхода газа через один из каналов температура в нем повысится и усилится геометрический напор, вовлекающий в этот канал все большее количество газа. Соблюдение же рассматриваемого правила в таком случае притормаживает случайное увеличение расхода газа в любом из вертикальных каналов и обеспечивает равномерное распределение газового потока.

Приведение в движение печных газов. Для того, чтобы привести в движение продукты сгорания топлива и удалить их из рабочего пространства и других элементов печи в атмосферу, необходимо преодолеть действие суммы всех сопротивлений на пути газового потока

где k – число случаев внезапных расширений каналов;

n – число местных сопротивлений;

q – число каналов, на которых имеют место потери напора на трение;

s – число вертикальных каналов, на которых возникает геометрический напор, противодействующий движению потока.

Естественная тяга осуществляется с помощью разрежения, т. е. геометрического напора, создаваемого дымовой трубой. Если пренебречь потерями в самой трубе, то её тяга определяется формулой

,

где Р_о, Р₁ – атмосферное давление на уровне основания трубы (Ро) и её устья (Р₁);

g = 9,81 – ускорение земного тяготения, м / с²;

- плотности окружающего воздуха и дымовых газов в трубе при их средних по высоте температурах t_B и t_Г, ⁰С, соответственно:

^,

где Н – высота дымовой трубы, м, причем и – плотности воздуха и дымовых газов при 0 ⁰С, кг / м³.

Высота трубы должна удовлетворять условию

.

Применяются и искусственные средства тяги в виде дымососов – отсасывающих вентиляторов с мощным электроприводом. Обычно дымосос устанавливают в зоне минимальной температуры дымовых газов, за котлом – утилизатором, использующим теплоту дымовых газов для получения водяного пара. При таких системах высота дымовой трубы ограничивается лишь санитарно-гигиеническими требованиями (но должна быть не ниже 16 м).

Струйное течение жидкостей и газов. Струя жидкости или газа, истекающая в неограниченное пространство (рис. 3.7), называется свободной. Если при этом струя распространяется в среде тех же физических свойств, то она называется затопленной. Границы свободной струи прямолинейны.

В зависимости от характера течения струи (ламинарное или турбулентное), за счет сил трения молекулярной или молярной природы, соответственно, струя вовлекает в движение вещество из окружающей среды. При этом разность давлений в струе и окружающей ее среде пренебрежимо мала. Давление Р в струе остается постоянным.

Рис. 3.7. Свободная струя

Для характеристики свойств струи используется понятие кратности увлечения:

^,

где Q_V1 и Q_V2 – объёмные расходы истекающей и увлекаемой сред на данном расстоянии от сопла, кг / с.

На протяжении начального участка струи (рис. 3.7) имеет место неразмытое ядро начальных скоростей W_O = W_MAX, м / с.

В дальнейшем на основном участке запас кинетической энергии струи , где m – масса вещества струи в данном её сечении, кг, постепенно сокращается в результате затрат энергии на увлечение струёй вещества из окружающей среды. В результате этого увлечения суммарный объёмный расход вещества в сечениях струи растет примерно пропорционально расстоянию от сопла.

Вследствие постоянства давления в струе количество движения во всех сечениях струи

^,

где ρ – плотность, кг / м³;

w – скорость в сечениях струи, м /с ;

f – площадь сечений струи на различных расстояниях от сопла, м².

В промышленных печах свободные струи встречаются редко. Так, пламя горящего газообразного топлива имеет значительно более высокую температуру, чем в остальном объёме рабочего пространства. Следовательно, физические свойства пламени отличаются от свойств окружающих пламя более холодных продуктов сгорания топлива. Вследствие отсутствия изотермичности пламени невозможно отнести его к категории затопленных струй. Кроме того, рабочее пространство печей заполнено нагреваемыми материалами и изделиями, и стесненное пространство не позволяет развиваться пламени как свободной струе.

К тому же свободным струям не позволяют развиваться элементы конструкции печей. Таким образом, в печах встречаются только ограниченные струи.

Сложный характер движения струйных потоков, особенно в местах их встречи с различными препятствиями, практически не позволяет исследовать явления механики струйных потоков в промышленных печах методами математического моделирования. Поэтому в рассматриваемой области особое значение приобрели физическое моделирование и его теоретическая основа – теория подобия [1, 3].