Вопросы для самопроверки к теме 2.2

1. В чем различие между стержневой и бесстержневой индукционными плавильными печами?

2. Как осуществляется нагрев и расплавление металла в тигельной бессердечниковой индукционной печи?

3. Как зависит глубина проникновения электрического тока в металл от магнитной проницаемости последнего?

4. Влияет ли частота переменного тока на глубину его проникновения в металл?

5. Как устроены электропечи типа электросопротивления?

6. Какой способ передачи теплоты нагреваемым телам превалирует в печах типа электросопротивления?

7. Для чего применяются силитовые нагреватели?

8. Для чего служит индуктор в печах индукционного нагрева?

Раздел 3. Элементы механики печных газов

Тема 3.1. Основные газовые законы

Печная теплотехника рассматривает газы: воздух, газообразное топливо, продукты сгорания топлива и др., - как сплошные среды, не касаясь их молекулярной природы. В этом отношении не делается различия между законами движения газов и жидкостей, тем более, что давление печных газов практически мало отличается от атмосферного.

И жидкости, и газы характеризуются такими физическими свойствами, как плотность, вязкость, теплопроводность, теплоемкость и ряд других. Различие между жидкостями и газами проявляется лишь при сверхвысоких давлениях, когда жидкости проявляют свою сжимаемость. Однако, давление газов в промышленных печах мало отличается от атмосферного, поэтому газы в рассматриваемой области считаются несжимаемыми средами, и различие между законами поведения газов и жидкостей, за редкими исключениями, отсутствует.

Основным уравнением состояния идеального газа является уравнение Менделеева – Клапейрона

PV = nRT,

где Р – абсолютное (полное) давление газа, Па;

V – занимаемый газом объем, м³;

n – количество газа в данном объеме, кмоль;

Т – абсолютная температура газа, К;

R = 8,314 – универсальная газовая постоянная, Дж/(кмоль^.К).

Уравнению Менделеева – Клапейрона можно придать несколько иную форму, более удобную для технических расчетов. Приняв общую массу газа М, кг, и его молярную массу m, кг / кмоль, получим

.

Для 1 кмоля газа имеем

РV = RT,

где V – удельный объём газа, равный 22,414, м³/кмоль (законн Авогадро).

Плотность газа, кг / м³,

^.

В идеальных газах и жидкостях силы взаимодействия между частицами (атомами, молекулами, ионами и проч.) отсутствуют.

Динамика газовых потоков. Реальные среды отличаются от идеальных наличием сил внутреннего трения между частицами газа (жидкости), или вязкости. Вязкость снижает скорость потока по мере приближения к стенке канала, где скорость W → 0, тогда как скорость потока идеального газа по всему сечению канала предполагается одинаковой.

В потоке реальных газов или жидкости, набегающем на плоскую поверхность какого-либо тела, между слоями среды, движущимися с различными скоростями на каждой элементарной площадке поверхностью 1 м² возникают касательные силы трения (рис. 3.1). Значение этих сил, согласно экспериментальному закону, установленному Ньютоном, выражается формулой, Н / м²,

^,

где – градиент скорости в направлении нормали (n) к поверхности;

– коэффициент динамической вязкости, .

Значение у жидкостей резко уменьшается с ростом температуры, а у газов – наоборот.

Существует также понятие кинематической вязкости, м²/с,

^.

Течение потока жидкости или газа в зависимости от соотношения сил инерции частиц и вязкости может быть ламинарным (слоистым) или турбулентным (вихревым).

На рис. 3.1 схематично представлены результаты опытов, иллюстрирующих переход из ламинарного течения (рис. 3.1, а) в турбулентное (рис. 3.1, б). Опыт заключается в том, что в поток воздуха вводится подкрашенный газ (или дым). При небольшой скорости потока воздуха струйки дыма длительное время не смешиваются с потоком воздуха, то есть имеет место ламинарное течение.

Эпюра скоростей потока в поперечном сечении канала при ламинарном течении имеет вид параболы, при которой максимальная скорость на оси канала оказывается вдвое выше средней по сечению (рис. 3.2, в).

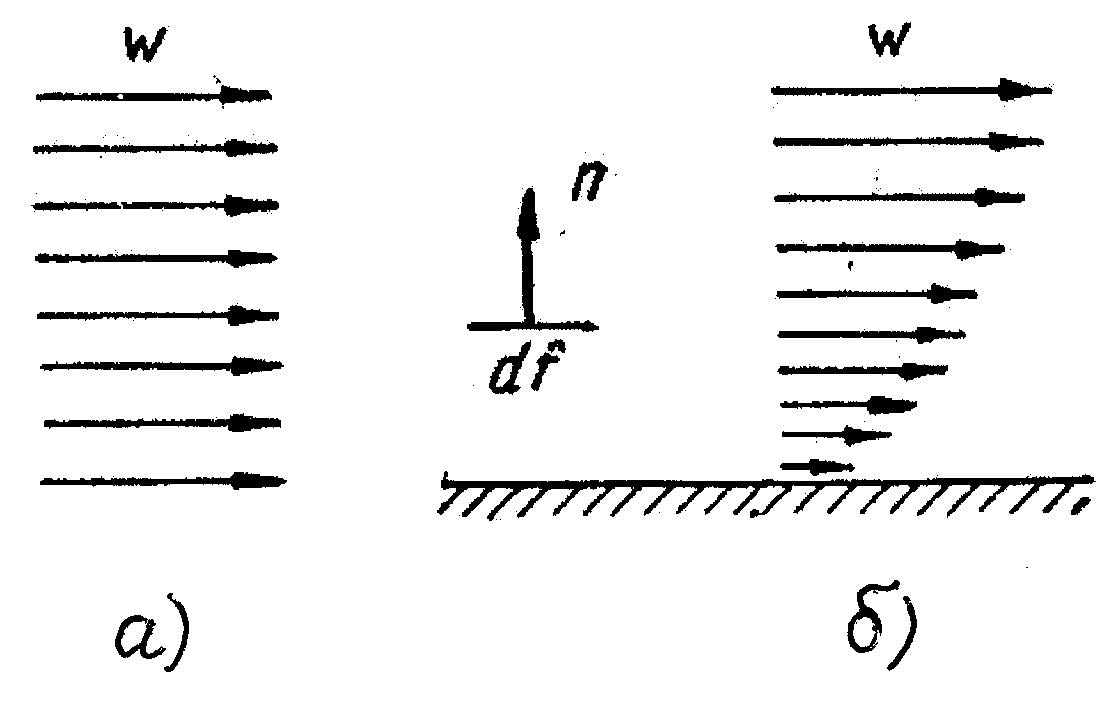
Рис. 3.1. Проявление вязкости среды при набегании на пластину

Если же увеличивать скорость потока воздуха, то ламинарное течение при определенных условиях переходит в турбулентное. При этом движение элементарных объемов потока (турбулентных молей) становится хаотическим, струйка дыма практически мгновенно распадается и становится видно, что отдельные частицы или струйки потока движутся не только вперед, но и поперек потока, вещество в котором интенсивно перемешивается.

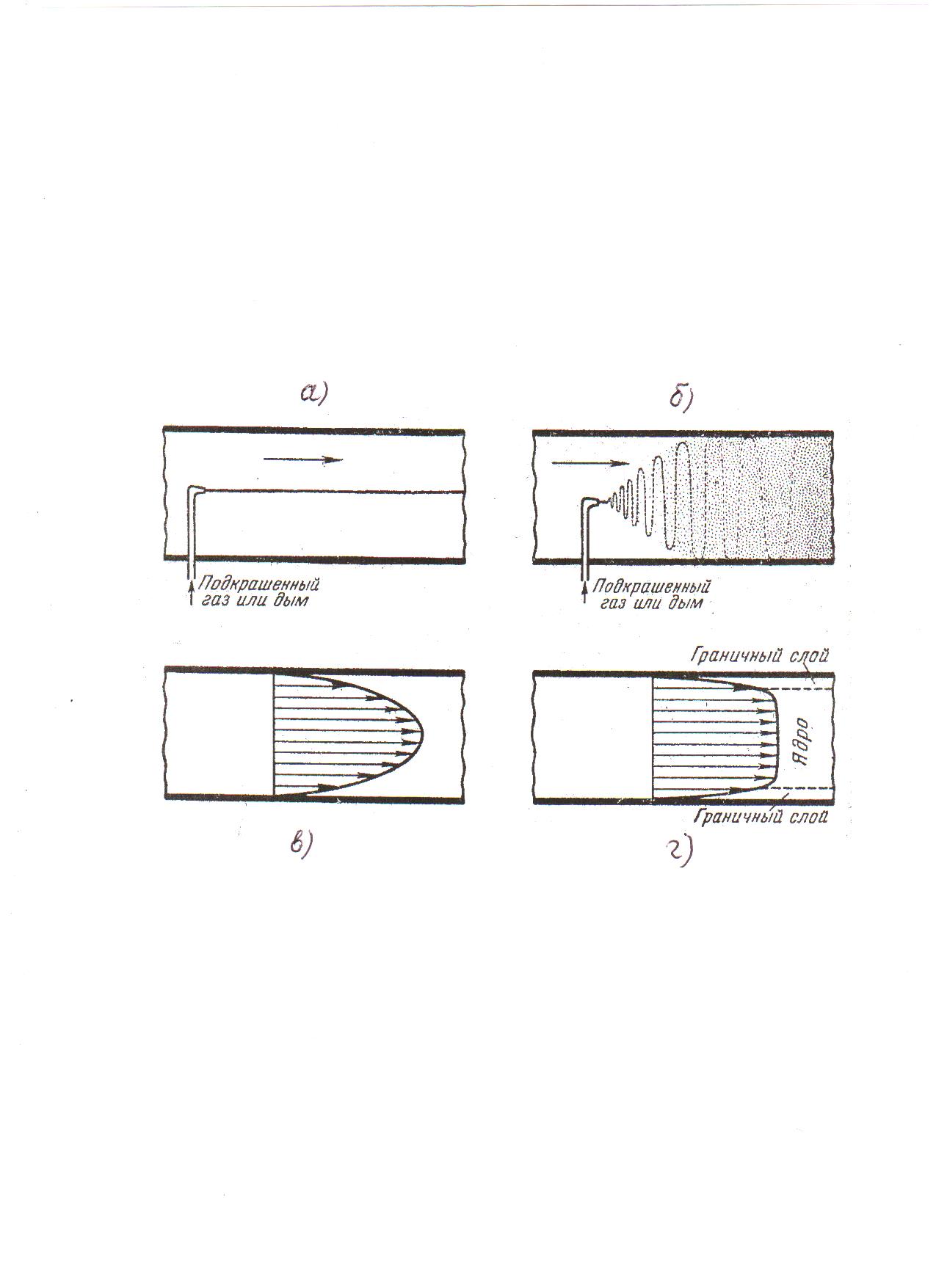
Рис. 3.2. Особенности ламинарного (слева) и турбулентного (справа) течения

Эпюра скоростей в поперечном сечении турбулентного потока по форме приближается к трапецеидальной (рис. 3.2,г), причём в начале образования турбулентности отношение средней по сечению скорости W_ср к максимальной W_max составляет

,

медленно увеличиваясь с ростом скорости течения.

Осборн Рейнольдс (1882, Великобритания) экспериментальным путем установил критерий перехода ламинарного течения в турбулентное и обратно. Этот безразмерный критерий, названный его именем, выражается формулой

^,

в которой W – средняя по сечению скорость потока, м/с; – коэффициент кинематической вязкости текущей среды, м² / с; D – гидравлический диаметр, м.

^,

где F – площадь поперечного сечения канала, м²; П – периметр канала, м.

Обычно считают критическим значением критерия (числа) Рейнольдса

Re_кр = 2300 … 2320.

При Re > Rе_кр, как правило, поток турбулентен, при Re < Re_кр – ламинарен.

Однако возможны исключения: если в потоке присутствуют частицы твердого вещества или воздействует вибрация, то турбулентность наступает при значениях Re, меньших критического. При отсутствии же возмущений ламинарный характер течения может сохраняться и при значениях Re, больших критического.

При расчетах явлений механики газов и жидкостей следует учитывать зависимость их плотности от температуры.

Для жидкостей, кг / м³

^,

где – плотности, соответственно при температурах t и t₀ = 0 ⁰C; β_ж – эмпирический коэффициент теплового расширения, зависящий от природы данной жидкости.

Для газов, кг/м³

^,

где – коэффициент теплового расширения, одинаковый для всех газов.