
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО АТОМНОЙ ЭНЕРГИИ
Снежинская Государственная Физико-Техническая Академия
А.Д.Зубов, в.Л.Соколовская
Математический анализ
В вопросах и ответах
Издание 2-е, переработанное и дополненное
Учебное пособие Снежинск
2009
УДК 517.0
Математический анализ в вопросах и ответах. Изд. 2-е, перераб. и доп. / сост. А.Д.Зубов, В.Л.Соколовская. - Снежинск: СГФТА, 2009. – 67 с.
"Математический анализ в вопросах и ответах" является, по замыслу авторов, собранием фактов курса дифференциального и интегрального исчисления, которые студент-математик должен знать без обращения к справочникам и курсам лекций.
Пособие предназначается, в первую очередь, студентам и аспирантам физико-математических специальностей. Может представить интерес как справочное пособие для научных работников в области прикладной математики, гидродинамики, механики, физики.
Рецензент: Г.В.Байдин, кандидат физ.-мат. наук,
ведущий научный сотрудник РФЯЦ-ВНИИТФ
Утверждено на заседании кафедры «Прикладные физика и математика»
Одобрено методическим советом СГФТА
© Снежинская государственная физико-техническая академия
Содержание
Вопросы по математическому анализу 4
Ответы 14
Литература 72
Вопросы по математическому анализу
– Скажите, пожалуйста, куда мне
отсюда идти?
– А куда ты хочешь попасть? – ответил Кот.
– Мне все равно… – сказала Алиса.
– Тогда все равно, куда и идти, – заметил Кот.
– … только бы попасть куда-нибудь, –
пояснила Алиса.
– Куда-нибудь ты обязательно попадешь, –
сказал Кот. – Нужно только достаточно
долго идти.
/Л.Кэрролл. «Алиса в Стране чудес»/
Что такое необходимое условие, достаточное условие, необходимое и достаточное условие? Примеры.
Какие типы определений используются в математике? Привести примеры.
Что такое множество, что является его элементами (точками)? Привести примеры.
Какие множества называются равными, что называется подмножеством?
Какое множество называется универсальным? Пустым? Привести примеры.
Что такое объединение множеств, их пересечение, разность, дополнение, симметрическая разность?
Сформулировать 12 свойств операций над множествами.
Дать определения: 1) декартового произведения множеств; 2) отображения множеств; 3) образа при отображении, прообраза элемента.
Дать определения: 1) образа множества, (полного) прообраза множества; 2) области определения, множества (или области) значений; 4) значения аргумента, значения функции в точке.
Дать определение функции.
Что такое сюрьективное, иньективное и биективное отображения? Какое отображение называется взаимно однозначным?
Дать определение эквивалентных (равномощных) множеств. Определение счётного множества. Примеры счетных и несчетных множеств.
Дать определение бинарного отношения. Примеры.
Что такое отношение эквивалентности? Перечислить его три свойства. Примеры и контрпримеры.
Классы эквивалентности. Теорема о двух классах эквивалентности множества. Фактор-множество. Примеры.
Дать определение мощности, или кардинального числа. Трансфинитные кардинальные числа.
Наименьшее трансфинитное кардинальное число. Теорема Кантора о множестве частей данного множества.
Континуум-гипотеза. Обобщённая континуум-гипотеза.
Определение вещественного числа. Основные свойства вещественных чисел (15 свойств).
Аксиома Архимеда (16-е свойство).
Свойство полноты множества вещественных чисел (17-е свойство). Точная верхняя грань или «супремум» множества. Двойственное ему понятие. Теорема о неполноте множества рациональных чисел.
Лемма об отделимости множеств на вещественной прямой.
Определение системы вложенных отрезков (СВО). Лемма о СВО.
Определение последовательности вложенных отрезков (ПВО) и стягивающейся ПВО. Лемма о стягивающейся ПВО.
В чем состоит метод математической индукции?
Фомулы бинома Ньютона и полинома Ньютона.
Неравенство Бернулли.
Сформулируйте определения:
а) расстояния
между точками в
 ;
;
б) открытого шара в ;
в) ограниченного
множества в
,
ограниченного сверху (снизу) множества
в
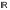 ;
;
г) неограниченного
сверху множества в
(с помощью кванторов
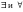 );
);
д) точной верхней (нижней) грани ограниченного сверху (снизу) множества в ;
е) внутренней точки множества, граничной точки;
ж) открытого множества, замкнутого;
з) связного множества;
и) окрестности точки;
к) области, замкнутой области;
л) предельной точки множества;
м) характеристической функции множества.
Сформулируйте определения:
а) числовой последовательности;
б) ограниченной и неограниченной последовательности;
в) предела последовательности, сходящейся последовательности.
Дайте геометрическую интерпретацию этих определений.
г) Сформулируйте теорему о пределе сходящейся последовательности.
в) Сформулируйте необходимое условие сходимости последовательности.
Сформулируйте принцип Больцано-Коши сходимости последовательности. Постройте отрицание этого принципа.
Сформулируйте определения:
а) бесконечно малой последовательности;
б) бесконечно большой последовательности.
Является ли любая неограниченная последовательность бесконечно большой?
Привести пример.
Сформулируйте теорему о трех последовательностях ("о двух милиционерах").
Сформулируйте теорему Штольца.
Сформулируйте:
а) определение монотонной последовательности;
б) признак сходимости монотонной последовательности.
Сформулируйте определения:
а) подпоследовательности;
б) предельной точки последовательности (дайте два определения и докажите их эквивалентность);
в) верхнего (нижнего) предела последовательности.
Сформулируйте теорему (лемму) Больцано-Вейерштрасса об ограниченной последовательности.
Сформулируйте два определения фундаментальной последовательности и докажите их эквивалентность. Дайте геометрическую интерпретацию этих определений.
Сформулируйте критерий Коши сходимости последовательности.
Сформулируйте определение предельной точки множества.
Сформулируйте определения (по Коши и по Гейне):
а) предела функции в точке и односторонних пределов;
б) предела функции в бесконечности.
Сформулируйте общий признак Больцано-Коши существования конечного предела функции (принцип сходимости). Постройте отрицание этого утверждения.
Сформулируйте определение непрерывности функции в точке. Какие точки называются точками разрыва функции?
Дайте определения точки устранимого разрыва и точек разрыва 1-го и 2-го рода.
Напишите два первых замечательных предела.
Какие функции называются элементарными?
Дайте определение бесконечно малой функции (б.м.ф.):
а) при
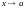 ;
;
б) при
 .
.
Приведите примеры.
Сформулируйте определение и приведите примеры б.м.ф.
 :
:
а) одного
порядка с функцией
 в точке а;
в точке а;
б) эквивалентной функции в точке а;
в) более высокого порядка при , чем .
Что
означает символическая запись
 при
?
при
?
Напишите асимптотические формулы для функций
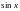 ,
,
 ,
,
 ,
,
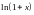 ,
,
 ,
,
 ,
,
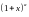 при
при
 .
.Напишите асимптотическую формулу Стирлинга для факториала числа
 .
.Дайте определение производной функции
 в точке
в точке
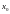 .
Каков физический и геометрический
смысл производной?
.
Каков физический и геометрический
смысл производной?Дайте определение дифференцируемости функции в данной точке.
Что такое дифференциал функции в данной точке? Каков его геометрический смысл?
Напишите производные простейших элементарных функций.
Чему равны производные:
а) произведения функций;
б) частного;
в) обратной функции;
г) сложной функции;
д) функции, заданной параметрически?
Чему равны n-е производные функций
 ?
?Что понимается под инвариантностью формы первого дифференциала?
Дайте определение ограниченной сверху (снизу) на множестве Х функции.
Сформулируйте 1-ю и 2-ю теоремы Больцано-Коши о непрерывных функциях.
Сформулируйте теорему о локальной ограниченности непрерывной функции.
Сформулируйте 1-ю и 2-ю теоремы Вейерштрасса о непрерывных на сегменте функциях.
Дайте определение равномерной непрерывности функции.
Сформулируйте теорему Кантора. Следствие.
Сформулируйте лемму Бореля о конечном покрытии.
Дайте определение возрастания (убывания) функции в точке и на промежутке.
Сформулируйте теорему, выражающую достаточное условие возрастания функции в точке.
Сформулируйте теорему, выражающую необходимое и достаточное условие монотонности дифференцируемой функции на промежутке.
Сформулируйте теорему, выражающую достаточное условие строгой монотонности функции на промежутке.
Сформулируйте теоремы Ферма, Дарбу, Ролля, Лагранжа, Коши. Каковы физическая и геометрическая интерпретации теоремы Лагранжа?
Сформулируйте правило Лопиталя раскрытия неопределенностей (3 случая).
Сформулируйте теорему о формуле Тейлора с остаточным членом:
а) в общей форме;
б) в форме Пеано;
в) в форме Лагранжа;
г) в форме Коши;
д) в интегральной форме.
Напишите разложения по формуле Маклорена функций , , , , .
Дайте определения и приведите примеры:
а) вертикальной асимптоты графика функции;
б) наклонной
асимптоты при
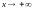 (аналогично
при
(аналогично
при
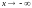 ).
).
Сформулируйте теорему о необходимых и достаточных условиях существования наклонной асимптоты.
Дайте определение локального экстремума функции. Сформулируйте необходимое условие экстремума и два достаточных условия.
Дайте определения:
а) направления выпуклости графика функции;
б) точки перегиба графика функции.
Сформулируйте:
а) необходимое условие перегиба;
б) достаточное условие.
Приведите примеры.
Приведите схему построения графика функции.
Что такое определенный интеграл?
Напишите формулу (формулы) среднего значения.
Дайте определение первообразной для функции
 на промежутке Х.
на промежутке Х.Напишите основные неопределенные интегралы.
Напишите формулы замены переменной и интегрирования по частям.
Сформулируйте правило Лейбница о дифференцировании определенного интеграла по параметру.
Что такое простая незамкнутая (замкнутая) кривая?
Дайте определение предела длин ломаных при
 .
Что такое спрямляемая кривая? Длина
кривой?
.
Что такое спрямляемая кривая? Длина
кривой?По каким формулам вычисляется длина кривой:
а) заданной параметрически;
б) в декартовых координатах;
в) в полярных координатах?
Что такое плоская фигура? Квадрируемая фигура? Площадь плоской фигуры?
По каким формулам вычисляется площадь фигуры:
а) заданной параметрически;
б) в декартовых координатах;
в) в полярных координатах?
Что называется телом? Что такое кубируемое тело? Объем тела?
По какой формуле вычисляется:
а) объем тела с известными поперечными сечениями;
б) объем тела вращения?
Какое множество называется счетным? Что такое множество мощности континуума?
Когда говорят, что числовой ряд сходится? Что такое сумма ряда?
Сформулируйте необходимый признак сходимости ряда.
Сформулируйте признаки Даламбера и Коши и интегральный сходимости рядов.
Сформулируйте признак Лейбница для сходимости знакочередующихся рядов.
Сформулируйте достаточный признак сходимости знакопеременного ряда. Какие ряды называются абсолютно, какие условно (неабсолютно) сходящимися? Привести примеры.
Какой ряд называется функциональным? Что называется областью сходимости функционального ряда?
Какой функциональный ряд называется:
а) мажорируемым;
б) равномерно сходящимся?
Что можно сказать о сумме ряда непрерывных функций, мажорируемого на некотором отрезке?
Сформулируйте теоремы об интегрировании и дифференцировании функциональных рядов.
Напишите формулу для радиуса сходимости степенного ряда. Чему равен радиус сходимости ряда, полученного почленным дифференцированием данного степенного ряда?
Напишите общий вид тригонометрического ряда Фурье и формулы для определения его коэффициентов.
Сформулируйте теорему о достаточных условиях представимости функции рядом Фурье.
Дать определение функции двух (и нескольких) переменных.
Дать определения (в
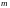 -мерном
пространстве): внутренней точки, открытой
области, точки сгущения, пограничных
точек, границы, замкнутой области.
Привести примеры открытых и замкнутых
областей.
-мерном
пространстве): внутренней точки, открытой
области, точки сгущения, пограничных
точек, границы, замкнутой области.
Привести примеры открытых и замкнутых
областей.Дайте определение предела функции многих переменных.
Сформулируйте теорему о связи между двойными и повторными пределами.
Дайте определение частной производной функции
 по аргументу
по аргументу
 во внутренней точке области определения
функции. Каков физический смысл частной
производной?
во внутренней точке области определения
функции. Каков физический смысл частной
производной?Что такое дифференциал функции в данной точке? От каких аргументов он зависит? Что понимается под инвариантностью формы первого дифференциала?
Сформулируйте теорему о достаточных условиях равенства смешанных производных нескольких переменных. Привести контрпример.
Дайте определение экстремума функции нескольких переменных.
Сформулируйте необходимые условия экстремума. Стационарные точки.
Сформулируйте достаточные условия существования (или отсутствия) экстремума функции двух переменных.
Какая функция называется неявной? Сформулируйте теорему о существовании неявной функции и правило ее дифференцирования.
Дайте определение функции, зависимой от других функций в некоторой области. Определения зависимости и независимости функций.
Сформулируйте теорему о достаточном условии независимости функций; общую теорему о зависимости и независимости функций.
Сформулируйте определение условного экстремума функции.
Напишите формулы перехода от прямоугольных координат
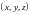 к цилиндрическим координатам
к цилиндрическим координатам
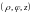 .
Вычислите якобиан перехода. Что
представляют собой координатные
поверхности
.
Вычислите якобиан перехода. Что
представляют собой координатные
поверхности
 и координатные линии
и координатные линии
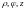 ?
?Напишите формулы перехода от прямоугольных координат к сферическим координатам
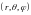 .
Вычислите якобиан перехода. Что
представляют собой координатные
поверхности
.
Вычислите якобиан перехода. Что
представляют собой координатные
поверхности
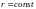 ,
,
 ,
,
 и координатные линии
и координатные линии
 ,
,
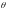 ,
,
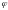 ?
?Напишите формулу для вычисления объема тела в криволинейных координатах. Что такое элемент объема в криволинейных координатах? Каков геометрический смысл якобиана отображения?
Сформулируйте определения:
а) интегральных сумм для криволинейного интеграла 1-го рода;
б) предела этих сумм;
в) криволинейного интеграла 1-го рода.
То же для криволинейного интеграла 2-го рода.
Напишите формулу Грина и сформулируйте условия, при которых она верна.
Назовите способы задания поверхности.
Дайте определение гладкой поверхности. Напишите уравнения касательной плоскости к поверхности в данной точке и вектора нормали.
Дайте определение поверхностного интеграла 1-го рода.
Дайте определение поверхностного интеграла 2-го рода. Определение общего поверхностного интеграла 2-го рода. Каков его физический смысл?
Какая область называется поверхностно односвязной? Приведите примеры поверхностно односвязных областей и областей, не являющихся поверхностно односвязными.
Дайте определение скалярного и векторного полей и приведите примеры физических полей.
Что такое поверхности (линии) уровня, векторные линии?
Дайте определение производной по направлению для скалярного и векторного полей. Как связана производная по направлению с частными производными?
Дайте определение градиента скалярного поля. Как связана производная по направлению
 с градиентом скалярного поля в данной
точке?
с градиентом скалярного поля в данной
точке?Какое векторное поле называется потенциальным? Приведите примеры потенциальных полей.
Дайте определение дивергенции векторного поля. Каков физический смысл дивергенции?
Дайте определение ротора векторного поля. Каков физический смысл ротора?
Какое векторное поле называется безвихревым? Приведите примеры безвихревых полей.
Какое векторное поле называется соленоидальным? Приведите примеры соленоидальных полей.
Что такое скалярный потенциал; векторный потенциал?
Напишите систему уравнений Максвелла. Какое из уравнений Максвелла выражает факт отсутствия магнитных зарядов?
Что такое оператор Гамильтона?
Запишите с помощью оператора Гамильтона:
а) градиент скалярного поля;
б) дивергенцию векторного поля;
в) ротор векторного поля;
г) формулы для производной скалярного и векторного полей по направлению .
Что такое полная производная; локальная производная; конвективная производная? Что они характеризуют и каким соотношением связаны?
Перечислите повторные дифференциальные операции в скалярных и векторных полях.
Результаты каких повторных дифференциальных операций тождественно равны нулю?
Что такое оператор Лапласа и как он связан с оператором
 ?
?Приведите примеры функций, удовлетворяющих уравнению Лапласа
 .
Как называются такие функции?
.
Как называются такие функции?Объясните, как представить произвольное векторное поле в виде суммы потенциального и соленоидального полей.
Что называется потоком векторного поля через поверхность? Напишите выражения для потока в векторной форме и в прямоугольных координатах.
Приведите примеры потоков физических векторных полей через заданные поверхности.
Запишите формулу Остроградского-Гаусса в прямоугольных координатах и в векторной форме. Сформулируйте условия, при которых она справедлива. Каков физический смысл формулы Остроградского-Гаусса?
Какая область называется объемно односвязной? Приведите примеры объемно односвязных областей и областей, не являющихся объемно односвязными.
Сформулируйте закон сохранения интенсивности векторной трубки для соленоидального поля.
Дайте инвариантное (независимое от выбора системы координат) определение дивергенции векторного поля.
Что называется циркуляцией векторного поля вдоль кривой? Напишите выражение для циркуляции в векторной форме и в прямоугольных координатах.
Запишите формулу Стокса в прямоугольных координатах и в векторной форме. Сформулируйте условия, при которых она верна. Каков физический смысл формулы Стокса?
Сформулируйте необходимое и достаточное условие потенциальности поля а(М) в поверхностно односвязной области и напишите формулу вычисления потенциала поля а(М).
Дайте инвариантное (независимое от выбора системы координат) определение ротора векторного поля.
Ответы
– А ты здесь откуда? – спросила Королева. – И куда
это ты направляешься? Смотри мне в глаза!
Отвечай вежливо! И не верти пальцами!
/Л.Кэрролл. «Алиса в Зазеркалье» /
– Располагая этой информацией, вы сможете прийти
к какому-нибудь правильному заключению.
/Записки о Ш.Холмсе. «Знак четырех»/
Необходимое условие – условие правильности утверждения А, без выполнения которого утверждение А заведомо не может быть верным.
Достаточное условие – условие, при выполнении которого утверждение А заведомо верно.
Необходимое
и достаточное условие
(критерий)
– утверждение А,
которое одновременно необходимо и
достаточно для правильности некоторого
другого утверждения В
(т.е. можно доказать как теорему
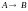 ,
так и обратную теорему
,
так и обратную теорему
 ).
).
Примеры: 1) существование предела функции в точке – необходимое условие её непрерывности в этой точке (но не достаточное!), 2) равенство предела функции в точке её значению в этой точке – необходимое и достаточное условие её непрерывности в этой точке (по самому определению непрерывности), 3) дифференцируемость функции в точке – достаточное условие её непрерывности в данной точке, 4) стремление к нулю общего члена ряда – необходимое (но не достаточное!) условие сходимости ряда.
Имеется два основных типа определений в математике: 1) логически строгое сведение определяемого объекта к уже введенным понятиям; 2) описательное определение с помощью слов разговорного языка.
Примеры: 1) окружность, как плоская кривая, все точки которой находятся на данном расстоянии r от фиксированной точки С (1-й тип), 2) множество (2-й тип), см. ниже.
Множество – это совокупность объектов любой природы. Объекты, образующие в своей совокупности данное множество, называются его элементами или точками.
Примеры: множество всех стульев в аудитории, множество-собрание богов на древнегреческом Олимпе, всех натуральных чисел, множество всех чётных чисел, множество всех простых чисел, множество всех кругов на плоскости, множество всех правильных многогранников и т.д.
Два множества называются равными, если они состоят из одних и тех же элементов. Если все элементы множества
 принадлежат множеству
принадлежат множеству
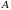 ,
то
называется подмножеством
множества
,
и пишут:
,
то
называется подмножеством
множества
,
и пишут:
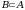 (или
(или
 ).
).
Некоторое фиксированное множество
 ,
если все рассматриваемые в данном
контексте множества являются его
подмножествами, называется универсальным.
Например,
для множества натуральных чисел,
множества действительных чисел,
множества квадратных матриц универсальным
будет некое общее числовое множество.
,
если все рассматриваемые в данном
контексте множества являются его
подмножествами, называется универсальным.
Например,
для множества натуральных чисел,
множества действительных чисел,
множества квадратных матриц универсальным
будет некое общее числовое множество.
Пустым множеством называется множество, не содержащее ни одного элемента. Пустое множество является подмножеством любого множества из .
Множество
 называется объединением
множеств
называется объединением
множеств
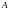 и
и
 ,
если оно состоит из тех и только тех
элементов, которые принадлежат хотя
бы одному из указанных множеств.
,
если оно состоит из тех и только тех
элементов, которые принадлежат хотя
бы одному из указанных множеств.
Пересечением
множеств
и
называется множество
 ,
состоящее из всех элементов, принадлежащих
одновременно и
,
и
,
т.е. элементов, общих для этих множеств.
,
состоящее из всех элементов, принадлежащих
одновременно и
,
и
,
т.е. элементов, общих для этих множеств.
Разностью
 двух множеств
и
называется множество, состоящее из всех
элементов
,
не принадлежащих
.
двух множеств
и
называется множество, состоящее из всех
элементов
,
не принадлежащих
.
Множество
 называется дополнением
,
или дополнением
до
множества
.
называется дополнением
,
или дополнением
до
множества
.
Симметрической
разностью
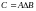 двух множеств
и
называется множество
двух множеств
и
называется множество
 .
.
Свойства операций над множествами:
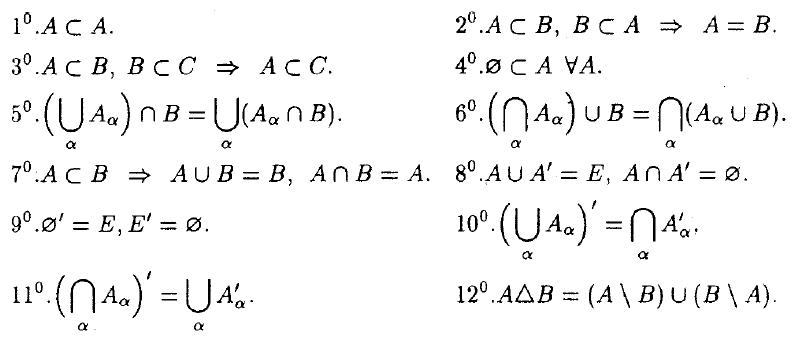
Декартовым произведением
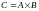 множеств
и
называют множество всех возможных пар
множеств
и
называют множество всех возможных пар
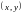 ,
где первый элемент
,
где первый элемент
 каждой пары принадлежит
,
а второй её элемент
каждой пары принадлежит
,
а второй её элемент
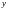 принадлежит
.
принадлежит
.
Подмножество
 декартова произведения двух множеств
декартова произведения двух множеств
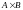 называется
отображением
множества
в множество
,
если выполнено следующее условие:
называется
отображением
множества
в множество
,
если выполнено следующее условие:
 пара
пара
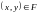 .
Напоминание:
квантор
.
Напоминание:
квантор
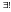 означает «существует единственный».
означает «существует единственный».
Пусть
отображение
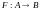 определяется так:
определяется так:
 ,
такое, что
.
Тогда элемент
,
такое, что
.
Тогда элемент
 называется образом
при
отображении
и записывается так:
называется образом
при
отображении
и записывается так:
 .
Элемент
называется прообразом
(одним
из возможных) элемента
.
.
Элемент
называется прообразом
(одним
из возможных) элемента
.
Множество
 всех элементов
всех элементов
 называется образом
множества
при отображении
,
т.е.
называется образом
множества
при отображении
,
т.е.
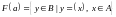 .
Для множества
.
Для множества
 само множество
при
отображении
называется (полным)
прообразом множества
С.
Множество
называется областью
определения,
а множество
само множество
при
отображении
называется (полным)
прообразом множества
С.
Множество
называется областью
определения,
а множество
 – множеством
(или областью)
значений.
Каждый элемент
– множеством
(или областью)
значений.
Каждый элемент
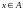 называется значением
аргумента
(или просто аргументом), а элемент
– значением
функции в точке
.
называется значением
аргумента
(или просто аргументом), а элемент
– значением
функции в точке
.
Функцией называется правило, по которому каждому элементу ставится в соответствие строго один элемент множества . Пишут: .
Отображение называется сюрьективным, или отображением «на» (т.е. отображением на ), накрытием, если
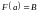 .
.
Отображение
называется инъективным,
или вложением,
если у каждой точки
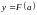 существует строго один прообраз, т.е.
из условия
существует строго один прообраз, т.е.
из условия
 следует, что
следует, что
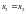 .
.
Отображение называется биективным, или взаимно однозначным, если оно одновременно является накрытием и вложением.
Множества и называются эквивалентными (равномощными), если между ними можно установить взаимно однозначное соответствие. Обозначается
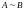 .
Счетным
множеством называется всякое множество,
эквивалентное множеству натуральных
чисел. Мощностью континуума
называется мощность множеств,
эквивалентных множеству всех
последовательностей, составленных из
нулей и единиц.
.
Счетным
множеством называется всякое множество,
эквивалентное множеству натуральных
чисел. Мощностью континуума
называется мощность множеств,
эквивалентных множеству всех
последовательностей, составленных из
нулей и единиц.Если на множестве задано множество всех пар
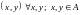 ,
удовлетворяющих некоторому отношению
(условию), то говорят, что на
задано бинарное
отношение.
,
удовлетворяющих некоторому отношению
(условию), то говорят, что на
задано бинарное
отношение.
Отношением эквивалентности называется бинарное отношение , обладающее тремя свойствами: а) рефлексивность:
 ;
б)
симметричность:
из
;
б)
симметричность:
из
 следует
следует
 ;
в)
транзитивность:
если
и
;
в)
транзитивность:
если
и
 ,
то
,
то
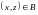 .
.Для произвольного
 множество
множество
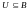 ,
состоящее из всех
,
эквивалентных
,
называется классом
эквивалентности.
Любые два класса эквивалентности либо
не пересекаются, либо совпадают.
Совокупность элементов, состоящих из
одного элемента (представителя) каждого
класса эквивалентности, называется
фактор-множеством.
,
состоящее из всех
,
эквивалентных
,
называется классом
эквивалентности.
Любые два класса эквивалентности либо
не пересекаются, либо совпадают.
Совокупность элементов, состоящих из
одного элемента (представителя) каждого
класса эквивалентности, называется
фактор-множеством.
Отношение « равномощно » является отношением эквивалентности между множествами. Класс эквивалентности, т.е. класс всех множеств, равномощных данному множеству, называется мощностью, или кардинальным числом. Конечные кардинальные числа являются классами эквивалентности конечных множеств. Эти числа по определению являются целыми натуральными числами и нулём: 0, 1, 2, ... Бесконечное кардинальное число, т.е. мощность бесконечного множества, называется трансфинитным кардинальным числом, или трансфинитным числом.
Мощность любого счетного множества равна мощности счётного множества
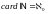 ,
которая является наименьшим
трансфинитным числом. Множество
,
которая является наименьшим
трансфинитным числом. Множество
 всех подмножеств множества
не равномощно ни самому множеству
,
ни его подмножеству (теорема
Кантора).
всех подмножеств множества
не равномощно ни самому множеству
,
ни его подмножеству (теорема
Кантора).
Согласно континуум-гипотезе,
 ,
где
,
где
 –
мощность счётного множества, является
кардинальным числом, непосредственно
следующим за
–
мощность счётного множества, является
кардинальным числом, непосредственно
следующим за
 .
Обобщённая
континуум-гипотеза
заключается в предположении, что при
любом кардинальном числе
.
Обобщённая
континуум-гипотеза
заключается в предположении, что при
любом кардинальном числе
 кардинальное число
кардинальное число
 непосредственно следует за
.
П.Коэн (1963) доказал неразрешимость
континуум-гипотезы (а, следовательно,
и обобщённой).
непосредственно следует за
.
П.Коэн (1963) доказал неразрешимость
континуум-гипотезы (а, следовательно,
и обобщённой).
Вещественное (или действительное) число – это конечная или бесконечная десятичная дробь, взятая со знаком «+» или «–».

Названия свойств:
Упорядоченность.
Транзитивность.
Существование суммы.
Ассоциативность суммы.
Коммутативность суммы.
Существование нуля.
Существование отрицательного (противоположного) числа.
Существование произведения.
Ассоциативность умножения.
Коммутативность умножения.
Существование единицы.
Существование обратного числа.
Дистрибутивность.
Упорядоченность по сумме.
Упорядоченность по умножению.
Аксиома Архимеда (16-е свойство):
160.
 такое, что
такое, что
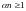 .
.
Свойство полноты множества вещественных чисел (17-е свойство).
170.
Для всякого непустого ограниченного
сверху множества
множество
его верхних граней
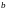 содержит минимальный элемент
содержит минимальный элемент
 ,
т.е. существует единственный элемент
,
т.е. существует единственный элемент
 такой, что 1)
–
верхняя грань множества
,
т.е. для всех
такой, что 1)
–
верхняя грань множества
,
т.е. для всех
 имеем
имеем
 ;
2)
–
наименьший элемент множества
,
т.е. для всех
;
2)
–
наименьший элемент множества
,
т.е. для всех
 справедливо неравенство
справедливо неравенство
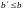 .
.
Элемент
называется точной
верхней гранью
или супремумом
множества
и обозначается
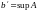 .
.
Аналогично определяется точная нижняя грань, или инфимум.
Теорема:
Множество
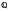 рациональных чисел не является «полным»,
т.е. для него не выполнено свойство 170.
рациональных чисел не является «полным»,
т.е. для него не выполнено свойство 170.
Для
любых вещественных
 ,
таких, что
,
таких, что
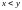 существует рациональное число
существует рациональное число
 такое, что
такое, что
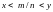 .
Аналогично, между любыми числами
существует иррациональное число.
.
Аналогично, между любыми числами
существует иррациональное число.
Лемма (об отделимости множеств). Пусть и – непустые множества на вещественной прямой, т.е.
 .
Пусть также для любых
и для любых
выполняется неравенство
.
Пусть также для любых
и для любых
выполняется неравенство
 .
.
Тогда
существует число
такое, что для всех
и для всех
имеет место неравенство
 .
.
Системой вложенных отрезков (СВО) называется множество
 ,
элементами которого являются отрезки,
причем такое, что для любых
,
элементами которого являются отрезки,
причем такое, что для любых
 имеем:
имеем:
 или
или
 .
.
Лемма
(о системе вложенных отрезков).
Пусть
– СВО. Тогда существует число
такое, что для любого отрезка
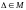 будем иметь
будем иметь
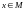 .
Это означает, что все отрезки
.
Это означает, что все отрезки
 имеют
общую точку
.
имеют
общую точку
.
Система вложенных отрезков (СВО) называется последовательностью вложенных отрезков (ПВО), если все эти отрезки занумерованы, причем отрезок с бОльшим номером содержится в каждом отрезке с меньшим номером.
Последовательностью
вложенных отрезков (ПВО) называется
стягивающейся
(ПСО),
если среди
входящих в неё отрезков найдутся отрезки
как угодно малой длины. Иначе говоря,
 в ПСО содержится и отрезок длиной меньше
в ПСО содержится и отрезок длиной меньше
 .
.
Лемма. Последовательность стягивающихся отрезков содержит общую точку и притом только одну.
Метод математической индукции:
а)
доказать утверждение для
 (обычно
(обычно
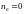 или 1);
или 1);
б)
доказать, что если утверждение верно
для
 ,
то оно верно и для
,
то оно верно и для
 .
.
Формула бинома Ньютона:
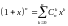 ,
где
,
где

– биномиальный коэффициент.
Формула
полинома
Ньютона для
 слагаемых:
слагаемых:
 .
.
Теорема (неравенство Бернулли). При
 и при натуральном
и при натуральном
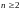 справедливо неравенство
справедливо неравенство
 .
.
а) Расстояние между точками
 и
и
 в
:
в
:
 .
.
б)
Множество
точек
 называется открытым
n-мерным
шаром радиуса
R
c
центром в точке А.
называется открытым
n-мерным
шаром радиуса
R
c
центром в точке А.
в)
Множество
 называется ограниченным,
если все его точки содержатся в некотором
шаре.
называется ограниченным,
если все его точки содержатся в некотором
шаре.
Определение
ограниченного
сверху
множества:  .
.
Определение
ограниченного
снизу
множества: 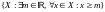 .
.
г)
Определение
неограниченного
сверху
множества:
 – отрицание определения ограниченного
сверху множества.
– отрицание определения ограниченного
сверху множества.
д)
Определение
точной
верхней грани
ограниченного сверху множества X:
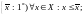
 ,
аналогично определяется точная нижняя
грань ограниченного снизу множества.
,
аналогично определяется точная нижняя
грань ограниченного снизу множества.
е) Точка А называется внутренней точкой множества {M}, если существует e-окрестность точки А (т.е. открытый шар радиуса e, с центром в точке А), целиком принадлежащая множеству {M}. Точка А называется граничной точкой множества {M}, если в любой e-окрестности точки А содержатся точки, как принадлежащие множеству {M}, так и не принадлежащие ему.
ж) Множество {M} называется открытым, если все его точки внутренние, замкнутым, если оно содержит все свои граничные точки.
з) Множество {M} называется связным, если любые две его точки можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
и) Окрестностью точки А называется любое открытое связное множество, содержащее точку А.
к) Областью называется открытое связное множество, объединение области и её границы – замкнутой областью.
л) Определение 1. Точка А называется предельной точкой множества {M}, если в любой e-окрестности этой точки содержатся точки множества {M}, отличные от А. Точка А может не принадлежать множеству {M}.
Определение 2. Точка А называется предельной точкой множества {M}, если любая окрестность этой точки содержит бесконечное подмножество множества {M}.
м)
Характеристической
функцией множества
{M}
называется функция
 ,
такая, что:
,
такая, что:
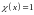 ,
если
,
если
 и
и
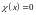 ,
если
,
если
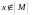 .
.
а) Говорят, что определена числовая последовательность (или просто последовательность) {xn}, если каждому натуральному числу n поставлено в соответствие некоторое число xn .
б)
Последовательность
{xn}
называется ограниченной,
если
 такое, что
такое, что
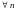
 .
С геометрической точки зрения это
означает, что все члены последовательности
находятся в некоторой окрестности
(М-окрестности)
точки
.
С геометрической точки зрения это
означает, что все члены последовательности
находятся в некоторой окрестности
(М-окрестности)
точки
 .
.
Последовательность
{xn}
называется неограниченной,
если

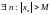 .
.
в)
Число
а
называется пределом
последовательности
{xn},
если

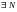 такое, что
такое, что

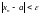 .
Обозначение:
.
Обозначение:
 .
С геометрической точки зрения это
означает, что в любой e-окрестности
точки а
находятся
все члены последовательности, начиная
с некоторого номера, зависящего, вообще
говоря, от ε.
.
С геометрической точки зрения это
означает, что в любой e-окрестности
точки а
находятся
все члены последовательности, начиная
с некоторого номера, зависящего, вообще
говоря, от ε.
Последовательность, имеющая предел, называется сходящейся.
г) Теорема. Сходящаяся последовательность имеет только один предел.
д) Теорема (необходимое условие сходимости последовательности).
Сходящаяся последовательность ограничена.
Теорема (принцип Больцано-Коши сходимости последовательности).
Для
существования конечного
предела
последовательности {xn}
необходимо и достаточно, чтобы
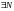 такой, чтобы неравенство
такой, чтобы неравенство
 выполнялось для всех
выполнялось для всех
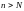 и
и
 .
.
а) Последовательность {xn} называется бесконечно малой, если
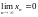 .
.
б) Последовательность {xn} называется бесконечно большой, если " A > 0 $ N такое, что " n > N |xn| > A .
В общем случае произвольная неограниченная последовательность не является бесконечно большой.
Теорема (о трёх последовательностях или "о двух милиционерах"). Если ,
 ,
и, начиная с некоторого номера n,
выполняются неравенства
,
и, начиная с некоторого номера n,
выполняются неравенства
 ,
то
,
то
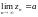 .
.
Теорема Штольца. Пусть:
 .
Тогда существует предел
.
Тогда существует предел
 .
.
а) Последовательность {xn} называется невозрастающей (неубывающей), если
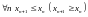 .
.
Невозрастающие
и неубывающие последовательности
называют монотонными
последовательностями. Последовательность
{xn}
называется возрастающей
(убывающей),
если
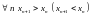 .
.
б) Теорема. Монотонная ограниченная последовательность сходится.
а) Последовательность
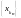 ,
где
,
где
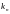 – произвольная возрастающая
последовательность целых положительных
чисел
– произвольная возрастающая
последовательность целых положительных
чисел
 ,
называется подпоследовательностью
последовательности {xn}.
,
называется подпоследовательностью
последовательности {xn}.
б) Два эквивалентных определения:
Определение 1. Число а называется предельной точкой (частичным пределом) последовательности {xn}, если из этой последовательности можно выделить подпоследовательность , сходящуюся к а.
Определение 2. Число а называется предельной точкой последовательности {xn}, если в любой e-окрестности точки а содержится бесконечно много членов последовательности {xn}.
в)
Наибольшая
(наименьшая) предельная точка
последовательности {xn},
ограниченной сверху (снизу), называется
верхним
(нижним)
пределом
этой последовательности и обозначается
 xn
(
xn
(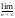 xn).
xn).
Теорема (теорема Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Два эквивалентных определения фундаментальной последовательности:
Определение
1.
Последовательность {xn}
называется фундаментальной,
если
 такое, что
и любого натурального числа p
выполняется неравенство
такое, что
и любого натурального числа p
выполняется неравенство
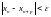 (в общем случае, для последовательности
точек
(в общем случае, для последовательности
точек
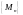 из
:
из
:
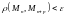 ).
).
Определение
2.
Последовательность {xn}
называется фундаментальной,
если
 такое, что
такое, что
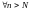 и
и
 выполняется неравенство
выполняется неравенство
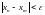 .
.
Геометрическая интерпретация этих определений: если последовательность {xn} фундаментальная, то такое, что расстояние между любыми двумя членами последовательности с номерами, большими, чем N, меньше e.
Теорема (критерий Коши сходимости последовательности). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Определение. Пусть X – область изменения числовой величины x. Точка а (a
 или а
или а
 )
называется предельной
точкой множества X,
если в любой e-окрестности
этой точки содержатся точки множества
X,
отличные от a.
)
называется предельной
точкой множества X,
если в любой e-окрестности
этой точки содержатся точки множества
X,
отличные от a.
а) Пусть a есть предельная точка множества Х – области определения функции .
Определение
1
(по
Коши). Число b
называется
пределом функции
в точке a
(при
),
если
 такое, что для
такое, что для
 ,
удовлетворяющего условиям
,
удовлетворяющего условиям
 ,
выполняется неравенство
,
выполняется неравенство
 .
.
Определение
2
(по
Гейне). Число b
называется
пределом функции
в точке a,
если для любой сходящейся к а
последовательности {xn}
такой, что
 ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
 сходится к b.
сходится к b.
Обозначение:
 или
или
 при
.
при
.
Отметим,
что функция может быть и не определена
в точке а,
т.е., вообще говоря,
 .
.
Определение
3
(по
Коши). Число b
называется
правым (левым) пределом функции f(x)
в точке a,
если
такое, что
,
удовлетворяющего условиям
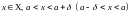 ,
выполняется неравенство
.
,
выполняется неравенство
.
Определение
4
(по
Гейне). Число b
называется
правым (левым) пределом функции f(x)
в точке a,
если для любой сходящейся к а
последовательности {xn}
такой, что
 ,
соответствующая последовательность
значений функции
сходится к b.
,
соответствующая последовательность
значений функции
сходится к b.
Обозначения:
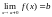 или
или
 (соответственно
(соответственно
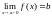 или
или
 ).
).
б)
Пусть функция
определена на полупрямой
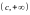 .
.
Определение
5
(по
Коши). Число b
называется
пределом функции
при

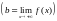 ,
если
,
если
 такое, что
такое, что
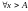 выполняется неравенство
.
выполняется неравенство
.
Определение
6
(по
Гейне). Число b
называется
пределом функции
при
,
если для любой бесконечно большой
последовательности {xn}
 соответствующая последовательность
значений функции
сходится к b.
соответствующая последовательность
значений функции
сходится к b.
Определения 5 и 6 эквивалентны.
Аналогично
определяется
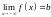 .
Если
.
Если
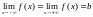 ,
то пишут
,
то пишут
 .
Например,
.
Например,
 .
.
Теорема (Принцип сходимости. Общий признак Больцано-Коши существования конечного предела функции).
Для
того чтобы функция
при стремлении x
к a
(a
может быть и
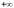 )
имела конечный предел, необходимо и
достаточно, чтобы для
)
имела конечный предел, необходимо и
достаточно, чтобы для
 такое, что неравенство
такое, что неравенство
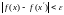 выполнялось, лишь только
выполнялось, лишь только
 и
и
 .
.
Определение 1. Функция , определенная в некоторой окрестности точки а, называется непрерывной в точке а, если
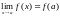 .
.
Пусть а – предельная точка области определения функции .
Определение 2. Точка а называется точкой разрыва функции , если в этой точке не является непрерывной.
Пусть определена в некоторой окрестности точки а, за исключением, быть может, самой точки а. Тогда а называется:
1)
точкой
устранимого разрыва функции
,
если
существует
,
но либо
не определена в точке а,
либо
 (если положить
(если положить
 ,
то функция
станет
непрерывной в точке а,
т.е. разрыв будет устранен);
,
то функция
станет
непрерывной в точке а,
т.е. разрыв будет устранен);
2)
точкой
разрыва I
рода функции
,
если существуют
 и
и
 ,
но
,
но
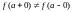 ;
;
3) точкой разрыва II рода функции , если в точке а не существует по крайней мере один из односторонних пределов функции .
Замечательные пределы: 1)
 ;
2)
;
2)
 ,
или
,
или
 .
.
Другие
часто встречающиеся пределы:
 .
.
Функции
 ,
,
 ,
,
 ,
,
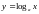 (
(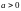 ,
,
 ),
),
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
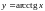
называются простейшими (или основными) элементарными функциями (к ним следует добавить гиперболические функции).
Функция называется элементарной, если она может быть получена с помощью конечного числа арифметических операций и суперпозиций над простейшими элементарными функциями.
Функция называется бесконечно малой (б.м.ф.) при (в точке а), если
 .
.
Аналогичные
определения имеют место для случаев
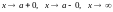 .
.
Функции и (
 в некоторой окрестности точки а)
называются:
в некоторой окрестности точки а)
называются:
а)
б.м.
одного порядка при
(в точке а), если
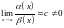 ;
;
б)
эквивалентными
б.м.
при
(в точке а), если
 (обозначение
(обозначение
 при
);
при
);
в)
функция
называется б.м.
более высокого порядка при
(в
точке а), чем
,
если
 .
.
Пишут
 при
.
при
.
Асимптотические формулы при :
-
 ,
,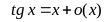 ,
, ,
,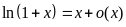 ,
,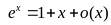 ,
,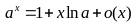 ,
,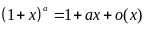 ,
, .
.
Асимптотическая формула Стирлинга:
 при
при
 .
Относительная ошибка убывает с
возрастанием
.
.
Относительная ошибка убывает с
возрастанием
.
Пусть функция
 определена в некоторой окрестности
точки
.
Приращением
этой функции в точке
называется следующая функция аргумента
определена в некоторой окрестности
точки
.
Приращением
этой функции в точке
называется следующая функция аргумента
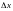 :
:
 .
.
Производной
функции
в точке
называется
 (если предел существует).
(если предел существует).
Физический смысл производной – скорость изменения функции в точке , геометрический – угловой коэффициент касательной к графику функции в точке
Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде
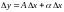 ,
где А
– некоторое число, а
,
где А
– некоторое число, а
 – функция аргумента
,
бесконечно малая и непрерывная в точке
– функция аргумента
,
бесконечно малая и непрерывная в точке
 (т.е.
(т.е.
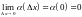 ).
).
Теорема.
Для того чтобы функция
была дифференцируемой в точке
,
необходимо и достаточно, чтобы существовала
производная
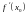 .
.
Отметим,
что при этом
 .
.
Дифференциалом (или первым дифференциалом) функции в точке (дифференцируемой в этой точке) называется следующая функция аргумента :
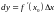 .
.
При
 дифференциал является главной
(линейной относительно
)
частью приращения функции в точке
.
дифференциал является главной
(линейной относительно
)
частью приращения функции в точке
.
Геометрический
смысл дифференциала
dy:
он равен приращению линейной функции,
графиком которой является касательная
в графику функции
в точке
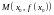 .
.
Таблица производных элементарных функций
функция |
производная |
функция |
производная |
функция |
производная |
C (постоянная) |
0 |
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) 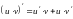 ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
n-е производные некоторых функций:
1.
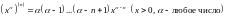 ;
;
2.
 ;
;
3.
 ;
4.
;
4.
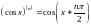 .
.
Инвариантность формы первого дифференциала: сохранение формулы в том случае, когда
 ,
но только теперь dx
является не произвольным приращением
аргумента х
(как
в случае, когда х
– независимая переменная), а дифференциалом
функции
в точке
,
но только теперь dx
является не произвольным приращением
аргумента х
(как
в случае, когда х
– независимая переменная), а дифференциалом
функции
в точке
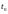 ,
т.е.
,
т.е.
 .
.
Определение. Функция называется ограниченной сверху (снизу) на множестве Х, если существует число М (m) такое, что
 выполняется неравенство
выполняется неравенство
 .
.
Первая теорема Больцано-Коши (об обращении непрерывной функции в нуль).
Пусть
функция
 определена и непрерывна в
определена и непрерывна в
 и на концах этого сегмента принимает
значения разных знаков. Тогда между a
и b
необходимо найдется точка с,
в которой функция обращается в нуль:
и на концах этого сегмента принимает
значения разных знаков. Тогда между a
и b
необходимо найдется точка с,
в которой функция обращается в нуль:
 .
.
Вторая теорема Больцано-Коши (о промежуточном значении).
Пусть
функция
определена и непрерывна в некотором
промежутке Х (замкнутом или нет, конечном
или бесконечном). Если в двух точках
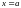 и
и
 (
( )
этого промежутка функция принимает
неравные значения
)
этого промежутка функция принимает
неравные значения
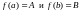 ,
то, каково бы ни было число С,
лежащее между А
и В,
найдется такая точка
,
то, каково бы ни было число С,
лежащее между А
и В,
найдется такая точка
 между а
и b,
что
между а
и b,
что
 .
.
Теорема (о локальной ограниченности непрерывной функции).
Если функция непрерывна в точке , то существует окрестность точки , в которой эта функция ограничена.
Теорема (1-я теорема Вейерштрасса).
Непрерывная на сегменте функция ограничена на этом сегменте.
Теорема (2-я теорема Вейерштрасса).
Непрерывная на сегменте функция достигает на этом сегменте своих точных граней, т.е.
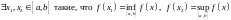 .
.
Определение. Функция называется равномерно непрерывной на множестве Х, если
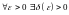 такое, что
такое, что
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 ,
выполняется неравенство
,
выполняется неравенство
 .
.
При равномерной непрерывности δ зависит только от ε и не зависит от x, в то время как при «обычной» непрерывности δ зависит как от ε, так и от x.
Теорема (теорема Кантора о равномерной непрерывности функции).
Непрерывная на сегменте функция равномерно непрерывна на этом сегменте.
Следствие.
Пусть функция
определена и непрерывна в
.
Тогда по заданному
 найдётся такое
найдётся такое
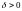 ,
что если сегмент произвольно разбить
на на частичные промежутки с длинами,
меньшими
,
что если сегмент произвольно разбить
на на частичные промежутки с длинами,
меньшими
 ,
то в каждом из них колебание функции
будет меньше
.
(Напоминание:
Колебанием
функции
в промежутке Х называется разность
,
то в каждом из них колебание функции
будет меньше
.
(Напоминание:
Колебанием
функции
в промежутке Х называется разность
 между её точными верхней и нижней
границами)
между её точными верхней и нижней
границами)
Лемма Бореля (о конечном покрытии).
Если сегмент покрывается бесконечной системой открытых промежутков, то из нее всегда можно выделить конечную подсистему, которая также покрывает этот сегмент.
Определение 1. Говорят, что функция возрастает в точке , если существует такая окрестность точки , в которой
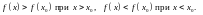
Аналогично определяется убывание функции в точке.
Определение
2.
Говорят, что функция
возрастает
(не убывает) на промежутке Х,
если
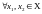 из условия
из условия
 следует неравенство
следует неравенство
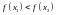 (соответственно
(соответственно
 ).
).
Аналогично определяется убывание (невозрастание) функции на промежутке.
Теорема (достаточное условие возрастания функции в точке).
Если
функция
дифференцируема в точке
и
 ,
то
возрастает (убывает) в точке
.
,
то
возрастает (убывает) в точке
.
Теорема (необходимое и достаточное условие монотонности функции на промежутке).
Для
того чтобы дифференцируемая на промежутке
Х функция
не убывала (не возрастала) на этом
промежутке, необходимо и достаточно,
чтобы
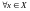 выполнялось неравенство
выполнялось неравенство
 .
.
Теорема (достаточное условие строгой монотонности функции).
Если
функция
дифференцируема на промежутке Х и
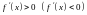 ,
то
возрастает (убывает) на промежутке Х.
,
то
возрастает (убывает) на промежутке Х.
Теорема Ферма. Пусть функция определена в некотором промежутке Х и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная
 в этой точке, то необходимо
= 0.
в этой точке, то необходимо
= 0.
Теорема
Дарбу.
Если функция
имеет конечную производную в промежутке
,
то функция
 принимает каждое промежуточное значение
между
принимает каждое промежуточное значение
между
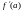 и
и
 .
.
Теорема Ролля. Пусть функция удовлетворяет условиям:
1) непрерывна на ;
2)
дифференцируема в
 ;
;
3)
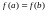 .
.
Тогда
существует точка
 такая, что
такая, что
 .
.
Теорема Лагранжа. Пусть функция удовлетворяет условиям:
1) непрерывна на ;
2) дифференцируема в .
Тогда
существует точка
такая, что
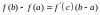 .
Последняя формула называется формулой
Лагранжа
или формулой
конечных приращений.
.
Последняя формула называется формулой
Лагранжа
или формулой
конечных приращений.
Физическая интерпретация теоремы Лагранжа.
Запишем формулу Лагранжа в виде
 .
.
В
левой части – средняя скорость за время
 .
Тогда
формула
Лагранжа утверждает, что существует
такой момент времени
,
в который мгновенная
скорость
равна средней
скорости на временном отрезке
.
.
Тогда
формула
Лагранжа утверждает, что существует
такой момент времени
,
в который мгновенная
скорость
равна средней
скорости на временном отрезке
.
Геометрическая
интерпретация теоремы
Лагранжа.
Касательная к графику в некоторой точке
 параллельна прямой, проходящей через
концы графика (или совпадает с ней).
параллельна прямой, проходящей через
концы графика (или совпадает с ней).
Теорема
Коши.
Пусть функции
и
 удовлетворяют условиям:
удовлетворяют условиям:
1) и непрерывны на ;
2) и дифференцируемы в ;
3)
 .
.
Тогда
существует точка
такая, что
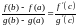 .
.
Последняя формула называется формулой Коши.
Правило Лопиталя (три основных теоремы).
Теоремы
1, 2 позволяют раскрывать неопределённости
вида
 .
.
Теорема 1. Пусть выполнены условия:
функции и определены и дифференцируемы в некоторой окрестности точки a (кроме, быть может, самой точки a);
 ;
; в
указанной окрестности точки a
(кроме, быть может, самой точки a);
в
указанной окрестности точки a
(кроме, быть может, самой точки a);существует
 .
.
Тогда
существует
 и он равен
.
и он равен
.
Теорема 2. Пусть выполнены условия:
функции и определены и дифференцируемы на полупрямой
 ;
; ;
; ;
;Существует
 .
.
Тогда
существует
 и он равен
.
и он равен
.
Теорема
3 позволяет раскрывать неопределенности
типа
 .
.
Теорема 3. Если выполнены условия 1), 3), 4) теорем 1 и 2, а вместо условия 2) выполнено условие
 (а
– число или символ
),
(а
– число или символ
),
то существует и он равен .
Теоремы 1, 2 и 3 справедливы также в отношении односторонних пределов.
Неопределённости
других типов
 можно свести к неопределенностям типа
или
и затем применять правило Лопиталя.
можно свести к неопределенностям типа
или
и затем применять правило Лопиталя.
Теорема 1. Если функция определена в некоторой окрестности точки и n раз дифференцируема в х0, то
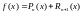 (формула
Тейлора),
где:
(формула
Тейлора),
где:
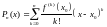 называется многочленом
Тейлора
для функции
(с центром в точке х0),
обладающим свойством
называется многочленом
Тейлора
для функции
(с центром в точке х0),
обладающим свойством
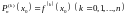 ,
а
,
а
 – остаточный член.
– остаточный член.
Теорема
2.
Пусть функция
определена в некоторой окрестности
точки х0
и
 раз дифференцируема в некоторой
окрестности точки х0.
Пусть х
– произвольное
значение аргумента из этой окрестности,
раз дифференцируема в некоторой
окрестности точки х0.
Пусть х
– произвольное
значение аргумента из этой окрестности,
 –
произвольное число. Тогда существует
точка
–
произвольное число. Тогда существует
точка
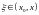 такая, что
такая, что
 .
.
Это выражение называется общей формой остаточного члена.
Другие, наиболее важные частные случаи:
а)
форма
Пеано
 ;
;
б)
форма
Лагранжа (p
= n+1):
 (
( );
);
в) форма Коши (p = 1):
 ;
;
г) интегральная форма:
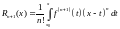 .
.
Разложения по формуле Маклорена (частный случай формулы Тейлора при
 )
некоторых функций:
)
некоторых функций:
|
|
|
|
|
|
Определение 1. Прямая называется вертикальной асимптотой графика функции , если хотя бы один из пределов
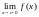 или
или
 равен
равен
 или
или
 .
.
Определение
2.
Прямая
 называется наклонной
асимптотой
графика функции
при
,
если эта функция представима в виде
называется наклонной
асимптотой
графика функции
при
,
если эта функция представима в виде
 ,
где
,
где
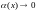 при
.
при
.
Аналогично
при
 .
.
Теорема. Для того чтобы прямая была наклонной асимптотой графика функции при , необходимо и достаточно, чтобы существовали пределы
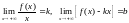 .
.
Аналогично при .
Определение. Функция имеет в точке локальный максимум (минимум), если существует такая окрестность точки , в которой при
 выполняется неравенство
выполняется неравенство
 (соответственно
(соответственно
 ).
Локальный максимум и локальный минимум
объединяются общим названием локальный
экстремум
(или просто экстремум).
).
Локальный максимум и локальный минимум
объединяются общим названием локальный
экстремум
(или просто экстремум).
Теорема (необходимое условие экстремума). Если функция имеет в точке экстремум, то производная в точке или равна нулю, или не существует.
Соответствующие значения аргумента, при условии, что в них функция непрерывна, называются точками возможного экстремума, или точками, подозрительными на экстремум.
Теорема (первое достаточное условие экстремума). Пусть функция дифференцируема в некоторой окрестности точки (за исключением, быть может, самой точки ). Тогда, если при переходе через точку (в сторону возрастания х) производная меняет знак с плюса на минус (с минуса на плюс), то в точке функция имеет локальный максимум (минимум). Если при переходе через точку производная функции не меняет знака, то в точке функция не имеет экстремума.
Теорема
(второе
достаточное условие экстремума).
Пусть в точке
возможного экстремума функция
имеет вторую производную. Тогда, если
 ,
то функция
имеет в точке
локальный максимум (минимум).
,
то функция
имеет в точке
локальный максимум (минимум).
Определение 1. График функции имеет на интервале выпуклость, направленную вниз (вверх), если в пределах интервала график лежит не ниже (не выше) любой касательной.
Определение
2.
Точка
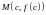 графика функции
называется точкой
перегиба
этого графика, если в этой точке график
функции имеет касательную и существует
такая окрестность точки с,
в пределах которой слева и справа от
неё направления выпуклости графика
функции
различны.
графика функции
называется точкой
перегиба
этого графика, если в этой точке график
функции имеет касательную и существует
такая окрестность точки с,
в пределах которой слева и справа от
неё направления выпуклости графика
функции
различны.
Теорема
(необходимое
условие перегиба).
Если график функции
имеет перегиб в точке
,
и вторая производная непрерывна в точке с,
то
непрерывна в точке с,
то
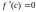 .
.
Теорема
(достаточное
условие перегиба).
Если в некоторой окрестности точки с
существует вторая производная функции
,
причем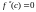 ,
и в пределах этой окрестности слева и
справа от точки с
знаки
различны, то график функции имеет перегиб
в точке
.
,
и в пределах этой окрестности слева и
справа от точки с
знаки
различны, то график функции имеет перегиб
в точке
.
Основная схема построения графика функции :
найти область определения функции и значения этой функции в точках разрыва и граничных точках области определения;
установить, имеет ли функция асимптоты;
установить, является ли функция четной, нечетной, периодической;
найти нули функции, т.е. решить уравнение
 .
Эти решения и точки разрыва функции
разбивают ее область определения на
промежутки знакопостоянства функции;
.
Эти решения и точки разрыва функции
разбивают ее область определения на
промежутки знакопостоянства функции;найти промежутки сохранения направления выпуклости и точки перегиба графика функции.
Интегральные суммы и определенный интеграл.
Пусть
функция
определена на сегменте
,
где
.
Обозначим через
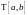 или просто Т произвольное разбиение
сегмента
точками
или просто Т произвольное разбиение
сегмента
точками
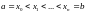 на n
частичных сегментов [xi-1,
xi]
(i=1,2,…,n).
Положим
на n
частичных сегментов [xi-1,
xi]
(i=1,2,…,n).
Положим
 ,
выберем на каждом сегменте [xi-1,
xi]
произвольную точку
,
выберем на каждом сегменте [xi-1,
xi]
произвольную точку
 и составим интегральную
сумму
и составим интегральную
сумму
 ,
соответствующую данному разбиению
и данному выбору промежуточных точек
.
,
соответствующую данному разбиению
и данному выбору промежуточных точек
.
Введем
обозначение
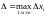 .
.
Определение
1.
Число I
называется пределом
интегральных сумм
 при
при
 ,
если
такое, что для всякого разбиения Т[a,b],
у которого
,
если
такое, что для всякого разбиения Т[a,b],
у которого
 ,
выполняется неравенство
,
выполняется неравенство  при любом выборе промежуточных точек
на
при любом выборе промежуточных точек
на
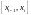 .
.
Определение
2.
Функция
называется интегрируемой
(по
Риману)
на
сегменте
,
если существует
 .
.
При
этом число I
называется определенным
интегралом
от функции
на сегменте
и обозначается
 .
.
Теорема (о среднем значении).
Пусть и интегрируемы на ,
 .
.
Тогда
существует число
 такое, что
такое, что
 .
.
Следствие
1.
Если положить
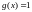 ,
то
,
то
 .
.
Число
 называется средним
значением функции
на сегменте
.
называется средним
значением функции
на сегменте
.
Следствие
2.
Если выполнены условия теоремы и функция
непрерывна, то
 такое, что
такое, что
 .
.
Следствие 3. Если функция непрерывна, то такое, что
 .
.
Определение 1. Функция
 называется первообразной
для функции
на промежутке Х, если
называется первообразной
для функции
на промежутке Х, если
 .
.
Определение
2.
Пусть функция
интегрируема на сегменте
.
Функция
 называется интегралом
с переменным верхним пределом.
называется интегралом
с переменным верхним пределом.
Теорема.
Непрерывная на сегменте
функция
имеет первообразную на этом сегменте.
Одной из первообразных является функция
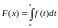 .
.
Таблица основных интегралов
Степенные функции |
Показательные функции |
|
|
|
|
Тригонометрические функции |
Гиперболические функции |
|
|
|
|
|
|
|
|
|
|
|
|
Дробные рациональные функции |
Иррациональные функции |
|
|
(для
|
( ) |
(для
|
(для
|
Теорема (Формула замены переменной).
Пусть
определена и непрерывна на
,
а
 определена и непрерывна вместе с
производной на
определена и непрерывна вместе с
производной на
 ,
где
,
где
 и
и
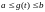 .
.
Тогда
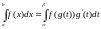 .
.
Теорема (Формула интегрирования по частям).
Если и имеют непрерывные производные на , то
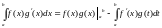 .
.
Теорема (правило Лейбница о дифференцировании определенного интеграла по параметру). Если функция
 и ее частная производная
и ее частная производная
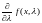 непрерывны на множестве
непрерывны на множестве
 ,
а функции
,
а функции
 и
и
 дифференцируемы на интервале
дифференцируемы на интервале
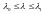 и удовлетворяют на нем условиям
и удовлетворяют на нем условиям
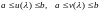 ,
то при
,
то при
 ,
,
 .
.
Первая
формула остается в силе и для несобственных
интегралов, если предположить, что
интеграл
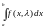 сходится, а интеграл
сходится, а интеграл
 равномерно сходится на интервале
.
(При этом функция
и ее производная
предполагаются непрерывными лишь на
множестве
равномерно сходится на интервале
.
(При этом функция
и ее производная
предполагаются непрерывными лишь на
множестве
 или на множестве
или на множестве
 .)
.)
Определение. Простой (плоской) незамкнутой кривой называется кривая L, заданная параметрически:
 ,
,
где
 – непрерывные на сегменте
функции, причем различным значениям
– непрерывные на сегменте
функции, причем различным значениям
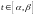 соответствуют различные точки
соответствуют различные точки
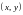 (т.е. нет кратных точек).
(т.е. нет кратных точек).
Если
точки
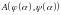 и
и
 совпадают, а остальные точки не являются
кратными, то кривая L
называется
простой
замкнутой кривой.
совпадают, а остальные точки не являются
кратными, то кривая L
называется
простой
замкнутой кривой.
Пусть L – простая (замкнутая или незамкнутая) кривая, заданная уравнениями . Рассмотрим произвольное разбиение сегмента точками
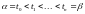 .
Ему соответствует разбиение кривой L
точками
.
Ему соответствует разбиение кривой L
точками
 ,
М1,
…,
,
М1,
…,
 ,
где
,
где
 .
Впишем в кривую L
ломаную АМ1М2…В.
Обозначим длину ломаной через
.
Впишем в кривую L
ломаную АМ1М2…В.
Обозначим длину ломаной через
 и положим
и положим
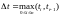 .
Число
l
называется пределом
длин ломаных
при
,
если
.
Число
l
называется пределом
длин ломаных
при
,
если
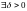 такое, что для любого разбиения сегмента
такое, что для любого разбиения сегмента
 ,
у которого
,
у которого
 ,
выполняется неравенство
,
выполняется неравенство
 .
.
Если существует предел длин ломаных при , то кривая L называется спрямляемой, а число l – длиной кривой L (или длиной дуги кривой L).
Длина кривой, заданной:
а)
параметрически:
 ;
;
б)
в декартовых координатах:
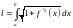 ;
;
в)
в полярных координатах:
 .
.
Плоской фигурой называется любое ограниченное множество точек плоскости.
Плоская
фигура называется квадрируемой,
если точная верхняя грань
 множества площадей всех вписанных
многоугольных фигур равна точной нижней
грани
множества площадей всех вписанных
многоугольных фигур равна точной нижней
грани
 множества площадей всех описанных
многоугольных фигур.
множества площадей всех описанных
многоугольных фигур.
Число
 называется площадью
плоской фигуры (по
Жордану).
называется площадью
плоской фигуры (по
Жордану).
Площадь плоской фигуры, заданной:
а)
в декартовых
координатах:
пусть плоская фигура представляет собой
криволинейную трапецию, ограниченную
непрерывными кривыми
 ,
(где
,
(где
 ),
и двумя отрезками прямых
),
и двумя отрезками прямых
 .
Тогда площадь фигуры вычисляется по
формуле
.
Тогда площадь фигуры вычисляется по
формуле
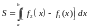 ;
;
б)
параметрически:
пусть граница плоской фигуры G
– простая замкнутая кривая, заданная
параметрическими уравнениями
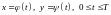 ,
причем точка
,
причем точка
 при изменении t
от
0 до Т
пробегает границу G
так,
что фигура G
остается
слева. Тогда площадь G
может
быть вычислена по любой из следующих
формул:
при изменении t
от
0 до Т
пробегает границу G
так,
что фигура G
остается
слева. Тогда площадь G
может
быть вычислена по любой из следующих
формул:
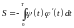 ,
,
 ,
,
 ;
;
в)
в
полярных координатах:
пусть плоская фигура представляет собой
криволинейный сектор, ограниченный
непрерывной кривой
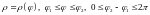 и отрезками лучей
и отрезками лучей
 .
Тогда площадь фигуры вычисляется по
формуле
.
Тогда площадь фигуры вычисляется по
формуле
 .
.
Телом называется любое ограниченное множество точек пространства.
Тело
называется кубируемым,
если точная верхняя
 грань множества объёмов всех вписанных
многогранников равна точной нижней
грани
грань множества объёмов всех вписанных
многогранников равна точной нижней
грани
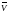 множества объёмов всех описанных
многогранников. (Многогранником
называется тело, состоящее из конечного
числа треугольных пирамид). Число
множества объёмов всех описанных
многогранников. (Многогранником
называется тело, состоящее из конечного
числа треугольных пирамид). Число
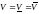 называется объёмом
тела (по
Жордану).
называется объёмом
тела (по
Жордану).
Пусть каждое сечение кубируемого тела плоскостью
 является квадрируемой фигурой, причём
её площадь
является квадрируемой фигурой, причём
её площадь
 является непрерывной функцией x
(
является непрерывной функцией x
( ).
Тогда
объём
этого тела вычисляется по формуле
).
Тогда
объём
этого тела вычисляется по формуле
 .
.
В
частном случае, когда тело является
телом вращения вокруг оси Ox
криволинейной трапеции, заданной
непрерывной функцией
,
,
объём тела вращения
вычисляется по формуле
 .
.
Множество называется счётным, если оно эквивалентно множеству натуральных чисел. Например, множество всех рациональных чисел. Если множество эквивалентно множеству всех вещественных чисел (которое не является счетным, точнее, оно является более мощным) сегмента
 ,
то говорят, что оно имеет мощность
континуума.
,
то говорят, что оно имеет мощность
континуума.
Выражение
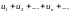 ,
где
,
где
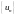 - бесконечная последовательность чисел,
называется числовым
рядом. Сумма
- бесконечная последовательность чисел,
называется числовым
рядом. Сумма
 называется n-й
частичной
суммой ряда. Если
существует конечный предел
называется n-й
частичной
суммой ряда. Если
существует конечный предел
 ,
то его называют суммой
ряда
и говорят, что ряд
сходится.
,
то его называют суммой
ряда
и говорят, что ряд
сходится.
Теорема (необходимый признак сходимости ряда).
Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
Теорема (Признак Даламбера).
Если
в ряде с положительными членами
отношение
 -го
члена к n-му
при
-го
члена к n-му
при
 имеет (конечный) предел l,
т.е.
имеет (конечный) предел l,
т.е.
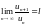 ,
то ряд сходится при
,
то ряд сходится при
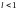 и расходится при
и расходится при
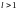 .
(В случае
.
(В случае
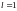 вопрос о сходимости остается открытым).
вопрос о сходимости остается открытым).
Теорема (Признак Коши).
Если
для ряда с положительными членами
величина
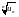 имеет конечный предел l
при
,
т.е.
имеет конечный предел l
при
,
т.е.
 ,
то ряд сходится при
и расходится при
.
(В случае
вопрос о сходимости остается открытым).
,
то ряд сходится при
и расходится при
.
(В случае
вопрос о сходимости остается открытым).
Теорема (Интегральный признак).
Пусть
члены ряда
положительны и не возрастают, т.е.
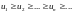 ,
и пусть
- такая непрерывная невозрастающая
функция, что
,
и пусть
- такая непрерывная невозрастающая
функция, что
 .
Тогда:
.
Тогда:
1)
если несобственный интеграл
 сходится, то сходится и рассматриваемый
ряд;
сходится, то сходится и рассматриваемый
ряд;
2) если указанный интеграл расходится, то расходится и ряд.
Теорема (признак Лейбница).
Если
в знакочередующемся
ряде
 члены таковы, что
члены таковы, что
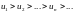 и
и
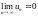 ,
то указанный ряд сходится, его сумма
положительна и не превосходит первого
члена.
,
то указанный ряд сходится, его сумма
положительна и не превосходит первого
члена.
Определение 1. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема (достаточный признак сходимости знакопеременного ряда).
Если
знакопеременный ряд
таков, что ряд
 сходится, то и данный знакопеременный
ряд также сходится.
сходится, то и данный знакопеременный
ряд также сходится.
Определение 2. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов . Если же знакопеременный ряд сходится, а ряд расходится, то данный знакопеременный ряд называется условно или неабсолютно сходящимся рядом.
Определение 1. Ряд называется функциональным, если его члены являются функциями от х:
 .
.
Определение 2. Совокупность значений х, при которых ряд сходится, называется областью сходимости этого ряда.
Определение 1. Функциональный ряд называется мажорируемым в некоторой области изменения х, если существует такой сходящийся числовой ряд
 с положительными членами, что для всех
значений х
из данной области выполняются соотношения
с положительными членами, что для всех
значений х
из данной области выполняются соотношения
 .
.
Определение
2.
Пусть
 – сумма функционального ряда
,
– сумма функционального ряда
,
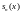 – сумма n
первых членов этого ряда. Функциональный
ряд называется равномерно
сходящимся
на отрезке
,
если для любого как угодно малого
– сумма n
первых членов этого ряда. Функциональный
ряд называется равномерно
сходящимся
на отрезке
,
если для любого как угодно малого
 найдется такой номер N
(не
зависящий от x),
что при всех
найдется такой номер N
(не
зависящий от x),
что при всех
 будет выполняться неравенство
будет выполняться неравенство
 для любого х
из
отрезка
.
для любого х
из
отрезка
.
Теорема. Сумма ряда непрерывных функций, мажорируемого на некотором отрезке , есть функция непрерывная на этом отрезке.
Теорема 1 (об интегрировании функциональных рядов).
Пусть ряд непрерывных функций мажорируется на некотором отрезке и пусть – сумма этого ряда. Тогда интеграл от в пределах от до х, принадлежащих отрезку , равняется сумме таких же интегралов от членов данного ряда.
Теорема 2 (о дифференцировании функциональных рядов).
Если
ряд
,
составленный из функций, имеющих
непрерывные производные на отрезке
,
сходится на этом отрезке к сумме
и ряд
 ,
составленный из производных его членов,
мажорируем на том же отрезке, то сумма
ряда производных равна производной от
суммы первоначального ряда, т.е.
,
составленный из производных его членов,
мажорируем на том же отрезке, то сумма
ряда производных равна производной от
суммы первоначального ряда, т.е.
 .
.
Радиус сходимости степенного ряда
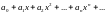 (определяется по признаку Коши):
(определяется по признаку Коши):
 .
Ряд, полученный почленным дифференцированием
данного степенного ряда, т.е.
.
Ряд, полученный почленным дифференцированием
данного степенного ряда, т.е.
 ,
имеет тот же интервал сходимости
,
имеет тот же интервал сходимости
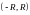 .
.
Функциональный ряд вида
 называется тригонометрическим
рядом.
называется тригонометрическим
рядом.
Пусть
периодическая с периодом
 функция
такова, что она представляется
тригонометрическим рядом, сходящимся
к данной функции в интервале
функция
такова, что она представляется
тригонометрическим рядом, сходящимся
к данной функции в интервале
 ,
т.е. является суммой этого ряда:
,
т.е. является суммой этого ряда:
 .
.
Если ряд мажорируем, то его можно почленно интегрировать в промежутке . В результате получаются коэффициенты Фурье:
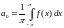 ,
,
 ,
,
 .
.
Тригонометрический ряд с такими коэффициентами называется рядом Фурье для функции .
Определение. Функция называется кусочно-монотонной на отрезке , если этот отрезок можно разбить конечным числом точек
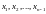 на интервалы
на интервалы
 так, что на каждом из интервалов функция
монотонна, т.е. либо невозрастающая,
либо неубывающая.
так, что на каждом из интервалов функция
монотонна, т.е. либо невозрастающая,
либо неубывающая.
Теорема (о достаточных условиях представимости функции рядом Фурье).
Если
периодическая с периодом
функция
– кусочно-монотонная на отрезке
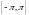 ,
то ряд Фурье, построенный для этой
функции, сходится во всех точках. Сумма
полученного ряда
равна значению функции
в точках непрерывности функции. В точках
разрыва
функции
сумма ряда равняется
,
то ряд Фурье, построенный для этой
функции, сходится во всех точках. Сумма
полученного ряда
равна значению функции
в точках непрерывности функции. В точках
разрыва
функции
сумма ряда равняется
 .
.
Определение. Переменная z (с областью изменения
 )
называется функцией
независимых
переменных
)
называется функцией
независимых
переменных
 из множества
,
если каждой паре
из множества
,
если каждой паре
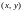 по некоторому закону или правилу
ставится в соответствие одно определённое
значение z
из
.
по некоторому закону или правилу
ставится в соответствие одно определённое
значение z
из
.
