2.3 Условиеи уравнения равновесия системы сходящихся сил.

Тело находится в равновесии в том случае, когда действующая на него система сил эквивалентна нулю.

При приведении системы сходящихся сил, было доказано, что такая система сил эквивалентна одной силе (равнодействующей или главному вектору).

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая (главный вектор) системы сил была равна нулю.

2.3.1 Геометрическое условие равновесия.

Главный вектор системы сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного на этих силах, поэтому, если при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил находится в равновесии.

Самозамыкание силового многоугольника данной системы сходящихся сил является геометрическим условием её равновесия.

Все эти выводы справедливы как для плоской, так и для пространственной системы сходящихся сил.

(12)

2.3.2 Аналитическое условие равновесия.

Аналитически модуль главного вектора в общем случае определяется формулой (10):

Под корнем стоит сумма положительных слагаемых, поэтому равнодействующая обратится в нуль только в том случае, когда ее проекции на координатные оси одновременно будут равны нулю.

Уравнения равновесия имеют вид:

(13)

Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Если все действующие на тело сходящиеся силы лежат в одной плоскости, то получаем только два уравнения равновесия:

(14)

Таким образом, простейший вид системы сходящихся сил – равнодействующая сила, приложенная в точке пересечения исходных сил.

Если равнодействующая системы сходящихся сил оказывается не равной нулю, то тело под действием такой системы сил будет двигаться в направлении равнодействующей (система сил не уравновешена). Для того чтобы уравновесить систему сил достаточно приложить силу, равную по модулю полученной равнодействующей и направленную по той же прямой в противоположную сторону (аксиома о двух силах).

Большое практическое значение имеет возможность использования этих условий и уравнений равновесия при решении практических задач.

Известно, например, что тело находится в равновесии вследствие наложенных связей. С помощью уравнений равновесия можно найти неизвестные величины, определяющие реакции связей.

Определение неизвестных величин возможно лишь в том случае, когда число неизвестных составляющих реакций не превышают числа уравнений равновесия, содержащих эти реакции. Такие системы называются статически определёнными системами, а задачи статически определимыми.

Для определенности решения пространственной задачи на равновесие системы сходящихся сил она должна содержать не более трех неизвестных, что соответствует трем уравнениям равновесия, а для плоской задачи – не более двух. В случае, если неизвестных реакций больше, чем уравнений равновесия, в которые входят эти реакции, то задача статически неопределимая и решить ее методами статики твердого тела невозможно.

Пример 1

К кронштейну АВС (рисунок 25) в точке В подвешены два груза – груз 1, вес которого G₁ =600 Н и груз 2, вес которого G₂ = 400 Н. Груз 2 подвешен через идеальный блок D. Стержни, блоки и тросы невесомы.

Определить усилия в стержнях АВ и ВС.

Рисунок 25

Решение:

1. Выбираем объект равновесия.

Объектом равновесия условимся называть тело (точку) или группу тел, связанных между собой, равновесие которых рассматривается.

В качестве объекта равновесия в данной задаче выбираем точку, в которой пересекаются линии действия заданных (активных) сил и , а также линии действия искомых реакций стержней АВ и СВ, поэтому объектом равновесия является узел В.

2. Прикладываем к этому узлу активные силы: вес , направленный вертикально вниз и вес , учитываем, что идеальный блок D изменяет направление силы, но не влияет на ее значение, поэтому вес направлен вдоль по тросу.

3. Применяя принцип освобождаемости от связей, заменяем действие на объект равновесия (узел В) мысленно отброшенных связей, которые осуществляются стержнями АВ и ВС. Прикладываем вместо стержней реакции стержней и , направляя их вдоль стержня от узла, то есть полагая, что в обоих стержнях АВ и ВС действуют растягивающие усилия (рисунок 26).

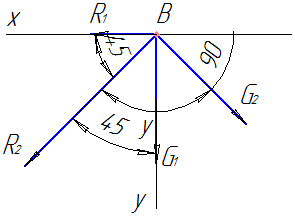
Рисунок 26

4. Выбираем положение системы координат. Начало координат совмещаем с точкой В. Ось Ох совмещаем с направлением линии действия реакции , а ось Оу направляем перпендикулярно оси Ох(при выбранном направлении осей большинство проекций на координатные оси имеет знак плюс).

5. Записываем выражение для определения равнодействующей силы в векторном виде:

6. Составляем уравнения равновесия в проекциях на выбранные координатные оси:

Решаем полученную систему уравнений. Из второго уравнения находим:

Из первого уравнения получим:

_R1= 400∙0,707 – (- 1249)∙0,707 = 1166

_Ответ:

_{R1=1166 [H]}

_{R2= -1249 [H]}

Знак минус перед численным значением реакции R₂ показывает, что стержень ВС не растянут, как предполагалось, а сжат. Действительное направление реакции противоположно направлению, обозначенному на чертеже.

Пример 2

Узел D неподвижно закреплен тремя невесомыми стержнями – АD, ВD и DС. К узлу привязана веревка, растягиваемая грузом . Крепления стержней шарнирные.

Определить усилия в стержнях, если ОВ=АВ=СЕ=30 см, ВD=40 см.

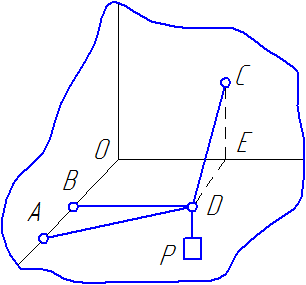
Рисунок 27

Решение:

1. Выбираем объект равновесия.

В качестве объекта равновесия в данной задаче выбираем точку, в которой пересекаются линии действия активной (заданной) силы , а также стержни АD,CD и ВD, поэтому объектом равновесия является узел D.

2. Применяя принцип освобождаемости от связей, заменяем действие на объект равновесия (узел D) мысленно отброшенных связей, которые осуществляются стержнями. Прикладываем вместо стержней реакции стержней , и направляя их вдоль стержня от узла, то есть полагая, что в стержнях действуют растягивающие усилия (рисунок 28).

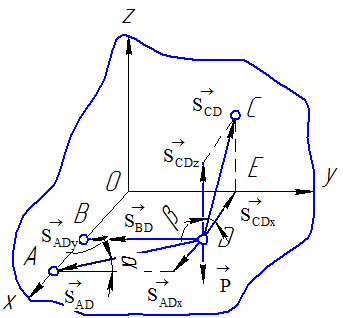
Рисунок 28

3.Выбираем положение системы координат. Начало координат совмещаем с точкой О.

4. Записываем выражение для определения равнодействующей силы в векторном виде:

₍₁₎

5. Стержни AD и CD наклонные, а значит и усилия также наклонные, поэтому прежде чем записать уравнения равновесия, запишем проекции на координатные оси.

Получим:

; (2)

; (3)

(4)

(5)

где:

(6)

(7)

(8)

(9)

Подставив формулы (6-9) в формулы (2-5), получим выражения:

₍₁₀₎

₍₁₁₎

₍₁₂₎

₍₁₃₎

6. Составляем уравнения равновесия в проекциях на выбранные координатные оси:

(14)

(15)

(16)

Из уравнения (16) определим

(17)

Из выражения (17), учитывая выражение (13), определим

_{Из уравнения (14) получим:}

₍₁₈₎

Учитывая выражение (10) и (12), получим:

(19)

_{Из выражения (1}9) определяем

₍₂₀₎

_{Подставив (20) и (7) в выражение (3), получим:}

Из выражения (15) получим:

(21)

Отсюда:

Ответ:

Знак минус перед численным значением усилия в стержне S_BD показывает, что стержень ВD не растянут, как предполагалось, а сжат. Действительное направление реакции противоположно направлению, обозначенному на чертеже.