Дидактические материалы

1. Действия над векторами

При решении задач статики обычно производят различные действия над скалярными или векторными величинами. При сложении и вычитании векторов окончательный результат зависит от модуля вектора и его направления. Результат сложения векторов называется векторной или геометрической суммой. Сложение двух векторов (сложение двух сходящихся сил) может быть произведено:

- по правилу параллелограмма – геометрическая сумма двух сил, (равнодействующая сила) приложенных в одной точке, приложена в точке их пересечения и равна по модулю и направлению диагонали параллелограмма, построенного на слагаемых векторах (силах) как на сторонах (рис. 1);

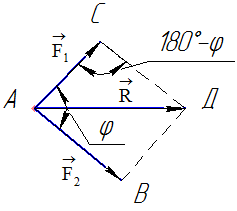
Рисунок 1

- по правилу треугольника – геометрическая сумма двух векторов по модулю и направлению соответствует замыкающей стороне треугольника, две другие стороны которого равны слагаемым векторам (рисунок 2).

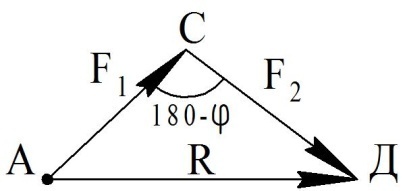
Рисунок 2

Определение равнодействующей двух сил по правилу параллелограмма или треугольника выражается векторным равенством ( ).

Оба приведенных правила можно использовать в следующих случаях:

- для графического решения задачи, при этом для построения параллелограмма или треугольника необходимо выбрать масштабный коэффициент;

- для графоаналитического решения с использованием геометрических свойств фигур или тригонометрических зависимостей.

Сложение большого числа векторов производится, как правило, построением силового многоугольника, являющемуся развитием правила треугольника: - геометрическая сумма векторов по модулю и направлению соответствует замыкающей стороне многоугольника, стороны которого равны слагаемым векторам ( ).

При помощи параллелограмма или треугольника сил можно решить и обратную задачу – разложить данную силу на две составляющие и , приложенные в той же точке и направленные по заданным линиям действия, (например, АВ и АС) (рисунок 3, рисунок 4).

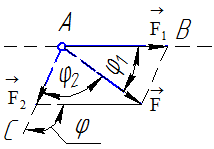
Рисунок 3

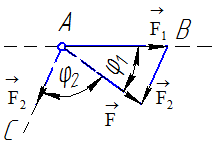
Рисунок 4

Результат вычитания двух векторов называется геометрической разностью.

Графический метод выполнения действий над векторами не всегда удобен, так как даже при самом тщательном построении результат получается не точным.

Поэтому, часто действия над векторами производится графоаналитическим способом, при котором модуль суммарного вектора (равнодействующая двух сил) определяется, в общем случае, по теореме косинусов (рисунок 5):

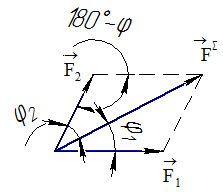
Рисунок 5

где: F₁и F₂ – модули данных слагаемых векторов (сил); -угол между направлениями сил F₁ и F₂.

_Учитывая, что cos(180⁰- )=(-cos ) получим:

или .

Модуль суммарного вектора относительно заданных векторов можно также определить по теореме синусов (рисунок 3):

В частном случае, если векторы и взаимно перпендикулярны, то параллелограмм превращается в прямоугольник и суммарный вектор определяется по теореме Пифагора (рисунок 6):

и

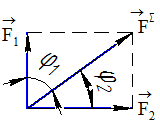
Рисунок 6

Наиболее общим способом определения модуля и направления равнодействующей системы сходящихся сил является аналитический метод.

Аналитический метод решения задач статики основывается на понятии о проекции силы на ось.

Проекция силы (как любого другого вектора) на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.

Осями координат служат две взаимно перпендикулярные оси, при этом, проектируемый вектор и его проекции на обе оси образуют прямоугольный треугольник.

Следует помнить основные правила проектирования:

- проекция вектора на ось есть скалярная величина;

- проекция силы на ось величина положительная, если сила направлена в сторону положительного направления оси или составляет с осью острый угол (рисунок 7);

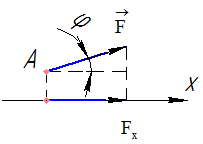
Рисунок 7

- проекция силы на ось величина отрицательная, если сила направлена в сторону противоположную положительному направлению оси или составляет с осью тупой угол (рисунок 8);

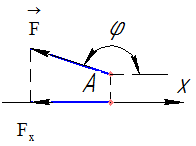
Рисунок 8

- проекция силы на ось равна нулю, если сила перпендикулярна оси (рисунок 9);

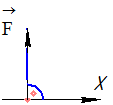
Рисунок 9

- модуль вектора определяется по его проекциями на две взаимно перпендикулярные оси по теореме Пифагора:

- направление вектора силы определяется по направляющим косинусам:

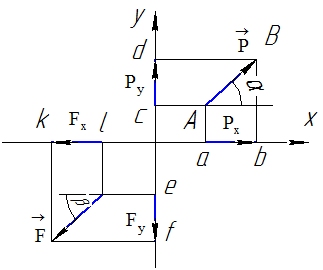
_{Таким образом, чтобы получить проекции силы на оси координат, необходимо из начала и конца вектора силы опустить перпендикуляр на каждую ось (рисунок 10). Отрезок оси между основаниями перпендикуляров, опущенных из начала и конца вектора силы, является проекцией силы на ось.}

_{Рисунок 10}

В случае, изображенном на рисунке 10, проекция силы на координатные оси Ох и Оу положительные, а проекции силы отрицательные:

,

_{В случае пространственной системы сил вектор силы проецируется на три взаимно перпендикулярные оси координат.}

Проекции вектора образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю.

Правило параллелепипеда используют также при разложении данной силы на составляющие, действующие по трем взаимно перпендикулярным осям.

Проекцией силы на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость (рисунок 11). В отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своими числовыми значениями, но и направлением в плоскости Оху.

По модулю проекция силы на плоскость Оху:

_{где α – угол между направлением силы и плоскостью Оху.}

_{Проекции силы на координатные оси:}

_;

_;

_;

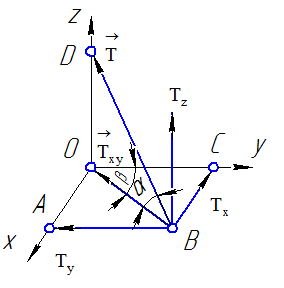
Рисунок 11