Вузел с

Направимо вісь Х по реакції R_1, а вісь Y – перпендикулярно їй.

Вказуємо всі кути, які будуть необхідні для проецирування:

Кути між R_{1 і} R₂ знаходимо з геометричних розмірів цієї конструкції (див. рис. 1а)

З Δ АКС : tg β = АК/ КС = 0,5/4 = 0,125 і β =7°

З Δ ВКС: tg (β + α) = ВК/КС = ¾ = 0,75 і α = 37°

Отже α = 37 – 7 = 30°

Кут між F і вісью Y дорівнює куту β =7°, так як кути з взаємно перпендикулярними сторонами.

3. Спроектувати всі сили та реакції вузла С на вибрані осі, скласти

рівняння рівноваги:

Σ Xi = - R₁ – R₂ cos30° - F₁ cos83° = 0 (1)

Σ Yi = – R₂ cos60° - F₁ cos7° = 0 (2)

_{З рівняння (2) визначаємо: R2 = - F1 cos7°/ cos60° = -10 * 0.99/0.5 = -19.8 Кн}

_{(Знак (-) вказує, що стержень стиснут силою 19,8 кН).}

_{З рівняння (1) визначаємо: R1 = - R2 cos30° - F1 cos83° =}

_{= -19.8 * 0.87 – 10*0.12 = 16 кН}

_{Зусилля в стержнях відповідно дорівнюють реакціям:}

_{N1 = R1 = 16 Кн (розтяг)}

_{N2 = R2 = 19,8 Кн (стискування)}

Для визначення зусиль в стержнях 3 і 4 вирізаємо вузол D

_{Для вузла D повторюємо усі дії з пункта 2.}

Вузел d

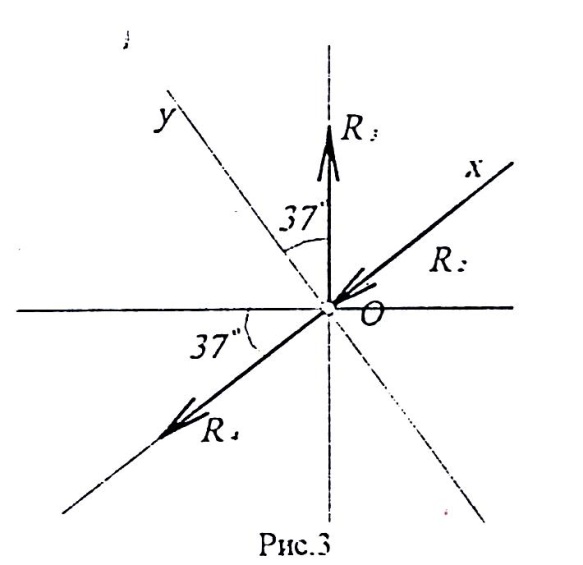
2. Направлення не відомих реакцій R₃ та R₄ приймаємо від вузла, вважаючи , що стержні розтягнуті. Зусилля R₂ = 19,8 кН направляємо до вузла, так як з попереднього розрахунку знаємо, що стержень 2 стиснут.

Направимо вісь Х по реакції R₄, а вісь Y – перпендикулярно їй.

Вказуємо всі кути, які будуть необхідні для проецирування:

Кут між горизонтом і R₄ дорівнює (β + α) = 37° (знаходимо з геометричних розмірів цієї конструкції див. рис. 1а)

Кут між R₃ і вісью Y дорівнює також 37°.

3.Спроектувавши всі сили та реакції вузла D на вибрані осі, складаємо

рівняння рівноваги:

Σ Xi = - R₄ – R₂ + R₃ cos53° = 0 (1)

Σ Yi = R₃ cos37° = 0 (2)

_{З рівняння (2) визначаємо: R3 = 0 – стержень не працює}

_{З рівняння (1) визначаємо: R4 = - R2 = -19,8 кН}

_{Зусилля в стержнях відповідно дорівнюють реакціям:}

_{N3 = R3 = 0}

_{N4 = R4 = 19,8 Кн (стискування)}

Графічний спосіб рішення

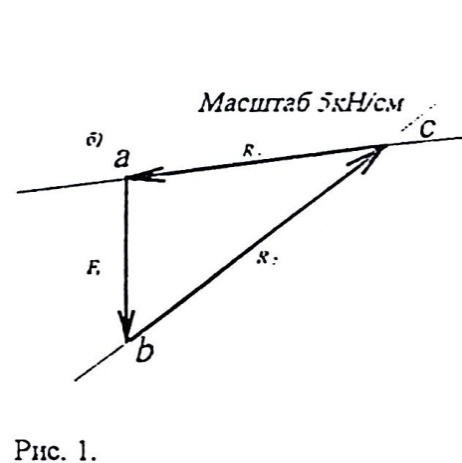
Визначимо цим способом зусилля в стержнях 1 і 2. З трьох сил, діючих в вузлі С, відома сила F₁ по модулю і напряму. Вибираємо масштаб сил, наприклад 5 кН в одному сантиметрі (Мсил = 5 кН/см) і будуємо силовий трикутник.

З любої точки в прийнятому масштабі відкладаємо силу F₁= 10 кН. З початку і кінця відрізка ab проводимо прямі, паралельні стержням 1 і 2, до їх перетину в точці С.

Отримуємо замкнутий силовий трикутник abс, в якому вектор ab = F₁,

вектор bс = R₂, вектор ас = R_1.

Вимірявши довжини сторін і помноживши на масштаб знаходимо відповідно сили в стержнях: _{N1 = R1 ≈ 16 кН; N2 = R2 = 19,8 кН}

Подумки перенісши напрям знайдених реакцій на відповідні стержні схеми конструкції, бачимо, що сила R₁ спрямована від вузла, а це означає, що стержень розтягнутий, сила R₂ спрямована до вузла, а отже стержень стислий.