Расчёт базы колоны.

Габариты квадратной в плане плиты базы назначаем минимальных размеров.

Выбираем базу с траверсами из листов толщиной t_tr=1,0см и вылетом плиты за пределы колонны с=11см.

Определяем габариты и площадь плиты.

Фактическое напряжение в бетоне фундамента под плитой:

.Принимаем бетон B15 R_пр.=12 МПа

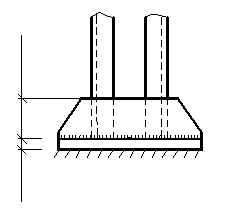
Рис. 18. К расчёту базы колонны.

Изгибающий момент на консольном участке плиты:

Для расчёта принимаем наибольший М_max= , по которому определяется толщина плиты:

Принимаем толщину плиты . Листы траверсы соединяем с поясами колонны угловыми сварными швами. Катет шва k_f=6 мм. Нижний и верхний концы колонны фрезеруем.

где n=4 – количество сварных швов (рис. 56); _f=0,7 – коэффициент глубины провара при ручной сварке.

Принимаем листы траверсы высотой равной h_tr=360 мм, что соответствует ГОСТ 82-70^*.

Толщина швов, соединяющих листы траверсы с плитой:

см,

где см – суммарная длина сварных швов (рис. 54).

Принимаем k_f=k_f.min=8 мм согласно [6, табл.38].

Таким образом, запроектированная база удовлетворяет требованиям прочности и жесткости.

Для соединения базы колонны с фундаментом принимаем 4 анкерных болта диаметром 20 мм.

Определяем расчётное сопротивление бетона фундамента:

.

Проверка общей устойчивости колонны.

Фактическая несущая способность колонны из швеллеров № 40

Устойчивость колонны из швеллеров № 40 не обеспечена, поэтому

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.

1. Металлические конструкции под общей редакцией Е.И. Беленя, Москва, Стройиздат 1986г.

2. СНиП II-23-81^* “Стальные конструкции”. Нормы проектирования Москва, Стройиздат 1990 г.

3. СНиП 2-01-85 “Нагрузки и воздействия”, Москва Стройиздат 1986г.

4. Нежданов К.К., Нежданов К.К., Бороздин А.Ю. Долговечные подкрановые конструкции. Учебное пособие. – Пенза: ПГУАС, 2010. – 222с.

Алгоритм расчёта поперечного сечения двутавровой балки

Балку двутаврового сечения формируем из трёх листов – стенки и двух поясов по запатентованному алгоритму [ ].

Из условия прочности на изгиб находим момент сопротивления

Определяем площадь сечения стенки t_ст. из условия прочности на срез

тогда минимальная толщина стенки при гибкости =130: .

Находим толщину стенки в зависимости от момента сопротивления при заданной гибкости её =130: 

назначаем толщину стенки кратно 0,2 см  t =1,6 .

Требуемая площадь сечения балки должна быть не менее

Площадь сечения стенки (50%) – , тогда  оптимальная высота

назначаем высоту стенки h_ст кратно 5 см  h_ст=215 см, а высоту сечения балки  см

Площадь пояса (25%) равна

Принимаем  t_п=3см, тогда см

Принимаем:  b_п = 57 см.

, 

Суммарная площадь сечения

.

Находим главный момент инерции и момент сопротивления.

.

Момент сопротивления .

Проверяем прочность главной балки при изгибе её:

,

прочность сечения главной балки при действии максимального изгибающего момента обеспечена.

Проверка прочности стенки балки на срез: .

Статический момент половины сечения равен:

 МПа

прочность на срез обеспечена.

Поверка прочности шва, соединяющего пояс со стенкой, на срез. Шов выполнен с полным проваром: Статический момент полки: .

Величина сдвигающих напряжений в сварном шве : прочность шва на срез обеспечена.

Относительный прогиб Жёсткость достаточна.

БАЛКА с поясами ИЗ тавров КТ9

16. Назначаем площадь сечения тавра

см²

принимаем два симметричных тавра КТ9: габарит hb = 21,7141,22 см;

масса m = 154кг/м;

площадь сечения каждого тавра A_Т = 196 см² ;

момент инерции J_x =5130 см⁴; z₀ =4,17 см;

толщина стенки тавра d=2,3 см;

толщина полки тавра t = 3,16 см.

17. Определяем высоту вставки при = 48766,3 см²

=21,71-4,17 = 17,54 см;

686-2·196=294 см²

18. Вычисляем высоту вставки, заменяя двутавр с поясами из листов на двутавр с поясами из тавров

= 184,07 см H = h_вст+ 2 h_Т H = 184,07+2·21,71 =227,5

=5546949,5

= 48764,4 см⁴

Точно

Формула изобретения

Способ увеличения момента инерции и момента сопротивления двутаврового, прокатного, стального профиля сечения, содержащего две полки соединённые стенкой, заключающийся в том, что упомянутый профиль сечения разрезают вдоль продольным резом на два тавровых профиля, раздвигают тавровые профили так, что между стенок тавров образуется зазор h _вст, вводят в зазор вставку из полосы стали по всей длине тавров, высоту сечения вставки определяют из квадратного уравнения

, где:

720-2·196=328 см²– площадь сечения вставки из полосы стали;

– ориентировочная площадь сечения стандартного тавра;

– расстояние от центра тяжести тавра до линии реза;

Отсюда вычисляем высоту вставки

Заменяем двутавр с поясами из листов на двутавр с поясами из тавров

Назначаем площадь сечения тавра

см²

принимаем два симметричных тавра КТ9: габарит hb = 21,7141,22 см;

масса m = 154кг/м;

площадь сечения каждого тавра A_Т = 196 см² ;

момент инерции J_x =5130 см⁴; z₀ =4,17 см;

толщина стенки тавра d=2,3 см;

толщина полки тавра t = 3,16 см.

Определяем высоту вставки при = 48766,3 см²

=21,71-4,17 = 17,54 см;

686-2·196=294 см²

гибкость его стенки, равная отношению высоты стенки к её толщине, не превышает предельную величину гибкости , обеспечивающую устойчивость стенки без промежуточных рёбер жёсткости и составляет 70 для малоуглеродистой стали и 60 для легированной стали, толщина стенки равна

;