4. Расчёт центрально сжатой колонны

Определяем размеры поперечного сечения трубчатой колонны, обеспечивающие устойчивость её.

Суммарная опорная реакция двух главных балок:

N = 2R_y = 2·21257,6 = 42515,2 гH

Сталь BC 3 сп 5 (R_у=230МПа)

Задаём коэффициент продольного изгиба  = 0,8

.

Высоту колонны определяем с учётом:

отметки настила по заданию – 8,5 м,

высоты главной балки h_гл.б=2,21м,

высоты второстепенной балки h_вт._б=0,45м

и глубины заделки плиты колонны ниже

нулевой отметки 0,2 м

8,5-2,21-0,45+0,2 = 6,04 м

Примем толщину стенки трубы t_o = 0,8 см

Площадь сечения трубы тонкостенной

, π

Принимаем трубу Ø 920·8 мм (92·0,8 см)

Фактическая площадь сечения трубы

,

радиус инерции i_x=i_у= = , по СНиП [1, С 9] коэффициент устойчивости

Проверка устойчивости.

1·0,967·230 =222,5 МПа

Вывод: устойчивость колонны обеспечена с запасом.

5. Расчёт базы центрально сжатой колонны.

Расчёт плиты базы колонны с фрезерованным торцом

Диаметр плиты = 92 + 18 = 110 см

Проверяем прочность бетона при смятии под плитой

;

По контактным напряжениям на смятие под плитой колонны назначаем бетон марки В15 МПа.

Прочность бетона В15 на смятие обеспечена.

Сталь плиты B Ст 3 Кп2 ГОСТ 380-71

R_у=195 МПа

Определяем толщину плиты из условия прочности её при изгибе

Напряжения в плите от изгиба её

По табл. 8.8 [1,с.204] находим коэффициенты в радиальном и тангенциальном направлении в зависимости от отношения диаметров

Находим изгибающие моменты в плите в радиальном и тангенциальном направлениях

Требуемый момент сопротивления при изгибе стальной плиты

.

Толщина стальной плиты должна быть не менее

Фактический момент сопротивления

Проверяем прочность стальной плиты при изгибе в радиальном и тангенциальном направлении:

; 

Прочность плиты достаточна.

Проверяем плиту на срез по контуру колонны.

Срезающая сила зависит от контактных напряжений сжатия N_ср= ·А_св

Площадь среза плиты по контуру колонны

;

<195 МПа

прочность плиты при изгибе по приведённым напряжениям достаточна.

Чугунная плиты базы

Диаметр чугунной плиты примем как у стальной = 92 + 18 = 110 см

Проверяем прочность бетона при смятии под чугунной плитой

;

По контактным напряжениям на смятие под чугунной плитой колонны назначаем бетон марки В15 МПа. Прочность бетона В15 на смятие обеспечена.

Принимаем чугун марки СЧ 30. Расчётное сопротивление чугуна при растяжении R_t =100 МПа.

Требуемый момент сопротивления при изгибе чугунной плиты СЧ 30

.

Толщина плиты должна быть не менее

Проверяем прочность чугунной плиты при изгибе в радиальном и тангенциальном направлении:

;

Площадь среза чугунной плиты по контуру колонны ; прочность плиты при сдвиге достаточна с избытком.

=84,3<100 МПа

прочность плиты при изгибе по приведённым напряжениям достаточна.

СОДЕРЖАНИЕ.

Расчёт настила.

Расчёт второстепенной балки.

Расчёт главной балки.

Расчёт колонны.

Расчёт базы колонны.

Расчёт стыка главной балки.

Снижение материалоемкости.

6. Расчёт монтажного стыка двутавра I 100Б4 на шпильках. Стык двутавра выполняем равнопрочным с основным сечением. Необходимо рассчитать равнопрочный стык прокатных двутавровых профилей I100 Б4 с соединениями шпильками. Шпильки выполнены по ГОСТ 22356-77* [4]. Сталь 40Х или 30Х3МФ “Селект” ГОСТ 4543-71* с наименьшим нормативным временным сопротивлением R_bun = 1350 МПа [4, с.72, табл. 61].

Алгоритм расчёта монтажного фрикционного стыка балки

Примем шпильки М20 или болты А_ш = 2,45 см [4, с.72, табл.62].

Расчётное сопротивление растяжению шпилек определяется по [4, с. 6]

Расчётное усилие , которое воспринимается одной поверхностью трения соприкасающихся пластин, равно

–	коэффициент условий работы болтов;
n = 1,12	коэффициент надёжности при зазоре между болтом и стенкой отверстия 1 мм;
	расчётное усилие, которое воспринимается одной поверхностью трения соприкасающихся пластин
	– расчётное сопротивление растяжению шпилек или болтов
=2,45 см2	– расчётное сопротивление растяжению шпилек или болтов
где  = 0,42	коэффициент трения при зачистке поверхностей газопламенным способом [4,с.41,табл.36*];

Несущая способность одного болта (2 поверхности трения)

F_вh=2Q_вh=2·781,4=1562,8 гН.

Характеристики двутавровой балки I 100 Б4 следующие:

площадь сечения А = 397 см²,

главный момент инерции J_x = 662170 см⁴;

момент сопротивления W_x = 13060 см³.

Сталь спокойной плавки С255 (ВСт3сп5) ГОСТ 27772-88 с расчётным сопротивлением R_y = 230 МПа [4,с.64,табл.51*], толщина t = 20…40 мм.

Фактический изгибающий момент который способен выдержать двутавр I 100 Б4 М_ф = R_y·W_x = 230·13060 = 3003800 гНсм.

Площадь полки двутавра А_п = 32,3·3,3 = 106,6 см²,

Площадь стенки А_ст = 94,8·1,86 = 176,33 см².

Момент инерции стенки двутавра

Часть изгибающего момента, воспринимаемая стенкой:

.

Требуемое плечо внутренней пары сил одного ряда болтов. Число рядов m=2, см.

Стык стенки перекрываем двумя симметричными накладками толщиной

t_нст = 1,2 см, 2t_н = 2·1,2 = 2,4 > t_ст = 1,86 см.

Зададим габарит болтового поля (рис. 1П6)

С = h_ст - 2 - 3d = 94,8 - 2·2 - 3·2 = 84,8 см,

где  = 2 см, d = 2 см.

Определяем число болтов n в ряду из квадратного уравнения

где коэффициент

n² – 12,56n + 13,56 = 0,

n = 11,37 шт. Примем 12 болтов.

Определяем шаг болтов S

S = = = 7,71 см.

Назначим шаг S = 7,7 см.

Уточняем габарит болтового поля

С = S(n – 1) = 7,7·11 = 84,7 см.

Определяем фактическое плечо внутренней пары сил одного ряда болтов

Фактическая несущая способность стыка стенки

Прочность стыка стенки достаточна.

Стык пояса.

Для стыка пояса примем три накладки толщиной по t_нп = 1,6 см (см. рис. 1П6)

А_н = 321,8 + 2·15·1,8 = 111,6  106,6 см².

Пояс двутавра выдерживает силу F_пф = 230·106,6 = 24518 гН.

Для стыка пояса необходимо число болтов

.

Примем 16 болтов М20 из стали 40Х “Селект” (болты с одной стороны от стыка). Шаг болтов принимаем минимальный S = 3d = 3·2 = 6 см.

Расчёт стержня решётчатой центрально-сжатой колонны

Расчётная сила, сжимающая колонну

где – грузовая площадь;

– расчётная нагрузка на рабочую площадку.

Определяем параметры колонны:

длина колоны:

примем коэффициент устойчивости , расчётное сопротивление R_y=230 МПа.

Определяем требуемую площадь поперечного сечения колонны относительно материальной оси X-X:

,

Принимаем сечение из двух балочных двутавров по гост 6020-83 2 I50 Б2: 2A= 2·102,2=204,4 см², )

Гибкость колонны относительно материальной оси X-X при :

Приведённая гибкость колонны

Проверяем устойчивость колонны

Фактическая несущая способность колонны из двух балочных двутавров 2 I50 Б2 (2A= 2·102,2=204,4 см², относительно оси X

Имеется запас по устойчивости 17,3%

Устойчивость колонны из двух балочных двутавров 2 I50 Б2 обеспечена.

Устойчивость колонны относительно оси X может быть проверена и так

Устойчивость колонны из двух балочных двутавров 2 I50 Б2 относительно оси X обеспечена.

Определим достаточную ширину колонны, при которой обеспечена равная устойчивость относительно осей X и Y.

Примем гибкость ветви меньше чем

Требуемая гибкость колонны относительно свободной оси Y

где ;

отсюда требуемый радиус инерции сечения: ,

то есть, расстояние от центра тяжести сечения колонны до центра тяжести каждого из двутавров должно быть не менее примем.

Находим момент инерции сечения колонны относительно свободной оси Y

радиус инерции

Гибкость колонны относительно оси Y

, Эффективная гибкость колонны относительно оси Y меньше чем относительно оси X. следовательно, устойчивость колонны относительно оси Y также обеспечена.

2012-9-18

Расчёт стержня решётчатой центрально-сжатой колонны (высокая)

Грузовая площадь (шарнирные опоры =1). Сталь: ГОСТ 2-777-2-88 В Ст3 сп5 (С255), расчётное сопротивление R_y=230 МПа. Расчётная нагрузка на единицу площади рабочей площадки .

Расчётная сила, сжимающая колонну:

Определяем высоту и расчётную длину колонны: .

Примем коэффициент устойчивости ,

Определяем требуемую площадь поперечного сечения колонны относительно материальной оси X: ,

Принимаем сечение из двух балочных двутавровых профилей 2 I55 Б2 по гост 6020-83: 2A= 2·124,75=249,5 см², ), J_y = 2760 см⁴.

Гибкость колонны относительно материальной оси X-X:

Приведённая гибкость колонны:

Проверяем устойчивость колонны

Несущая способность колонны из двух балочных двутавровых профилей 2 I50 Б2 (2A= 2·102,2=204,4 см², относительно оси X

Устойчивость колонны из двух балочных двутавровых профилей 2 I55 Б2 обеспечена. Имеется запас по устойчивости 39420/44367,89= 0,888 (11,1%).

Устойчивость колонны относительно оси X может быть проверена и так

Устойчивость колонны из двух балочных двутавров 2 I55 Б2 относительно оси X обеспечена. Имеется запас по устойчивости 158/177,8= 0,888 (11,1%).

Определим достаточную ширину колонны, при которой обеспечена равная устойчивость относительно осей X и Y.

Примем гибкость ветви меньше чем колонны

Требуемая гибкость колонны относительно свободной оси Y

где ;

отсюда требуемый радиус инерции сечения:

то есть, расстояние от центра тяжести сечения колонны до центра тяжести каждого из двутавров должно быть не менее примем.

Находим момент инерции сечения колонны относительно свободной оси Y

радиус инерции

Гибкость колонны относительно оси Y

, Эффективная гибкость колонны относительно оси Y меньше чем относительно оси X. следовательно, устойчивость колонны относительно оси Y также обеспечена.

2012-10-17

3.3. Расчёт планок, соединяющих ветви

Назначаем размер планки 40·40·1 см. Планки привариваем к ветвям колонны угловыми швами с катетом шва k_f = 8 мм и проверяем их прочность по сварному шву. Условная поперечная сила в колонне [ ]

где N=36420 гН - продольное усилие в колонне;  =  .

Определяем шаг планок:

, 1340-40 1300 (40см оголовок и база)

число шагов 1300/141 =9,2 примем 10 шагов s=1300/10=130cм.

Поперечная сила в ветви

поперечная сила, срезающая планку

Изгибающий планку момент , где a=26 см.

Момент сопротивления шва ;

Напряжения в шве при изгибе

Площадь поперечного сечения шва

= = 25,2 см, =45 см длина шва.

Сдвигающие напряжения .

Приведённые напряжения в шве

Прочность сварного шва по приведённым напряжениям по металлу шва обеспечена.

Проверки прочности шва по металлу границы сплавления не делаем, так как _z=1>_f=0,7 (см. СНиП II-23-81* [табл. 37]).

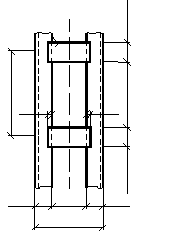
Рис. 17. К расчёту планок колонны.

Расчёт стержня решётчатой центрально-сжатой колонны

Расчётная сила, сжимающая колонну

где – грузовая площадь;

– расчётная нагрузка на рабочую площадку.

Определяем параметры колонны:

длина колоны:

примем коэффициент устойчивости , расчётное сопротивление R_y=230 МПа.

Определяем требуемую площадь поперечного сечения колонны относительно материальной оси X-X:

,

Принимаем сечение из двух балочных двутавров по гост 6020-83 2 I50 Б2: 2A= 2·102,2=204,4 см², )

Гибкость колонны относительно материальной оси X-X при :

Приведённая гибкость колонны

Проверяем устойчивость колонны

Фактическая несущая способность колонны из двух балочных двутавров 2 I50 Б2 (2A= 2·102,2=204,4 см², относительно оси X

Имеется запас по устойчивости 17,3%

Устойчивость колонны из двух балочных двутавров 2 I50 Б2 обеспечена.

Устойчивость колонны относительно оси X может быть проверена и так

Устойчивость колонны из двух балочных двутавров 2 I50 Б2 относительно оси X обеспечена.

Определим достаточную ширину колонны, при которой обеспечена равная устойчивость относительно осей X и Y.

Примем гибкость ветви меньше чем

Требуемая гибкость колонны относительно свободной оси Y

где ;

отсюда требуемый радиус инерции сечения: ,

то есть, расстояние от центра тяжести сечения колонны до центра тяжести каждого из двутавров должно быть не менее примем.

Находим момент инерции сечения колонны относительно свободной оси Y

радиус инерции

Гибкость колонны относительно оси Y

, Эффективная гибкость колонны относительно оси Y меньше чем относительно оси X. следовательно, устойчивость колонны относительно оси Y также обеспечена.

2012-9-18

СНИЖЕНИЕ МАТЕРИАЛОЁМКОСТИ главной балки

Введём шарниры в первом и третьем пролётах так, чтобы момент во втором пролёте и опорные моменты над двумя центральными колоннами стали равны друг другу

; ; ; ;

В середине центрального пролёта двухконсольной балки

Вылет каждой из консолей

Принимаем t_ст=1,3 см

= (63,3 %). Было 100 %

Вывод: Экономия стали 37,8%

А_ст=50% ; А_ст=217см² h_ст= А_ст=218,4 см²

А_nол=25% =108,5 см² А_пол=42·2,6=109,2 см²

=218,4 +2·109,2 = 436,8 > 434 см². Запас обеспечен.

Вывод: Прочность балки на изгиб обеспечена

Исправить

м

Q= гН

МПа

Вывод: прочность стенки на срез около опоры балки обеспечена.

Определяем материалоемкость

Было:

V=686·100=68600см³

m_1м=68600·7,85=538510г=538,5кг

m_1г.б.=538510·17,4=9370074г=9370кг

m_12г.б.=9370·12=112440кг=112,44т

Стало:

V=452·100=45200cм³

m_1м=45200·7.85=354820г=354,8кг

m_1г.б.=354,8·17,4=6173,5кг

m_12г.б.=6173,5·12=74082,2кг=74,082т

Вывод: Экономия материала составляет 34,1%

ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНКИ ГЛАВНОЙ БАЛКИ

Устойчивость стенки балки при локальных воздействиях сосредоточенных сил обеспечиваем, приваривая к ней автоматической сваркой одностороннее продольное ребро в верхней четверти высоты стенки.

Проверку устойчивости проводим по СНиП. Для этого определяем действующее напряжение в трёх сечениях по длине балки: около опоры, в месте изменения сечения и в середине пролёта балки и в этих же сечениях находим критические напряжения. Устойчивость зависит: от гибкости стенки (130…135); от схемы расположения рёбер жёсткости. Общая устойчивость главной балки обеспечена за счёт раскрепления верхнего пояса главной балки второстепенными балками.

Локальные напряжения

Условие, при котором обеспечивается устойчивость [ , с.28, ф.82]:

Локальные напряжения под опорами двух второстепенных балок

Q_{вт б}= 1445,1 гН

	Напряжения, МПа
	Нормальные	Нормальные	Сдвигающие
Около опоры	0	9,7	69
в середине пролёта		9,7	0
в месте изменения сечения	162,8	9,7	68,7

Критические напряжения:

нормальные [ , с.29, ф.84];

В нашем случае , поэтому, при вычислении и принимаем , тогда – отношение большей стороны пластинки к меньшей ;

= =1,13,

Во всех случаях сдвигающие напряжения вычисляем по действительным размерам пластинки: , – меньшая сторона пластинки ; сдвигающие напряжения определяем по формуле (76) с подстановкой в неё фактических размеров проверяемой пластинки;

– отношение большей стороны пластинки к меньшей

; (76)

в этой формуле (76) R_s= 0,57·R_y=133,4 МПа,

= =1,1277

, – длинная сторона пластинки

Локальные

Проверяем устойчивость стенки в сечении А-А, около опоры

<1 –

устойчивость обеспечена

Проверяем устойчивость стенки в сечении В-В, в середине пролёта

< 1

устойчивость обеспечена

Проверяем устойчивость стенки в сечении Б-Б, в месте изменения сечения

< 1 –

устойчивость обеспечена

Вывод: Устойчивость стенки по всей длине балки обеспечена.

Расчёт стержня решётчатой центрально сжатой колонны

Расчётная сила, сжимающая колонну

где – грузовая площадь;

– расчётная нагрузка на рабочую площадку.

Определяем параметры колонны:

длина колоны:

п римем , расчётное сопротивление R_y=230 МПа.

Определяем требуемую площадь поперечного сечения колонны относительно материальной оси X-X:

,

Принимаем сечение из двух балочных двутавров по

гост 6020-83 2 I45 Б2 ( см², )

Гибкость колонны относительно оси X-X при

:

Приведённая гибкость колонны

Проверяем устойчивость колонны

Фактическая несущая способность колонны из двух балочных двутавров 2 I45 Б2 (A=2^.86=172 см², i_x= 18,32 см) относительно оси X

Устойчивость колонны из двух балочных двутавров 2 I45 Б2 обеспечена. Имеется небольшой запас по устойчивости.

Проверка устойчивости колонны относительно оси X может быть проверена и так

Устойчивость колонны из двух балочных двутавров 2 I45 Б2 относительно оси X обеспечена.

Определим ширину колонны, при которой обеспечена равная устойчивость относительно осей X и Y.

Примем гибкость ветви меньше чем

Требуемая гибкость колонны относительно свободной оси Y

где ;

отсюда требуемый радиус инерции сечения: ,

то есть расстояние от центра тяжести сечения колонны до центра тяжести каждого из двутавров должно быть не менее примем.

Находим момент инерции сечения колонны относительно свободной оси Y

требуемый радиус инерции

Фактическая гибкость колонны относительно оси Y

, следовательно, устойчивость колонны относительно оси Y выше, чем относительно оси X, то есть устойчивость колонны обеспечена. 2011-10-10

3.3. Расчёт планок, соединяющих ветви

Назначаем размер планки 50·25·1 см. Планки привариваем к ветвям колонны угловыми швами с катетом шва k_f = 8 мм и проверяем их прочность по металлу сварного шва:

Условная поперечная сила в колонне [ ]

где N=35950 гН - продольное усилие в колонне;  = 0,914.

Определяем шаг планок:

, примем s=77cм.

Поперечная сила в ветви

поперечная сила, срезающая планку

Изгибающий планку момент

где a=26 см.

Рис. 17. К расчёту планок колонны.

Момент сопротивления шва

;

Напряжения в шве при изгибе

Площадь поперечного сечения шва

= = 24,5 см

=30 см – расчётная длина шва.

Сдвигающие напряжения .

Приведённые напряжения в шве

Прочность сварного шва по приведённым напряжениям по металлу шва обеспечена.

Проверки прочности шва по металлу границы сплавления не делаем, так как _z=1>_f=0,7 (см. СНиП II-23-81* [табл. 37]).