6. Нахождение собственных элементов положительно определенной матрицы

Приведем итерационный метод одновременного нахождения собственных значений и собственных векторов положительно определенной матрицы.

Ели действительная матрица

— симметрическая и положительно определенная, то:

1) корни λ₁, λ₂,…, λ_n характеристического уравнения

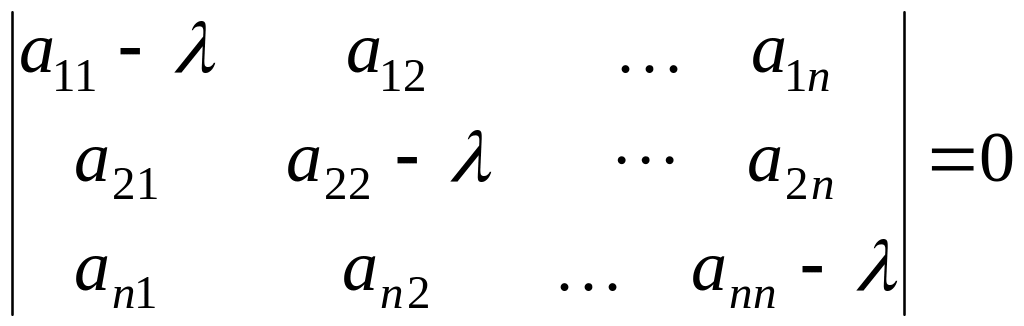(6.1)

действительны и положительны;

2) собственные векторы

, (j=1,2,…,n)

могут быть взяты действительными и удовлетворяют условиям ортогональности

при . (6.2)

Напишем систему, служащую для определения собственного вектора х⁽¹⁾:

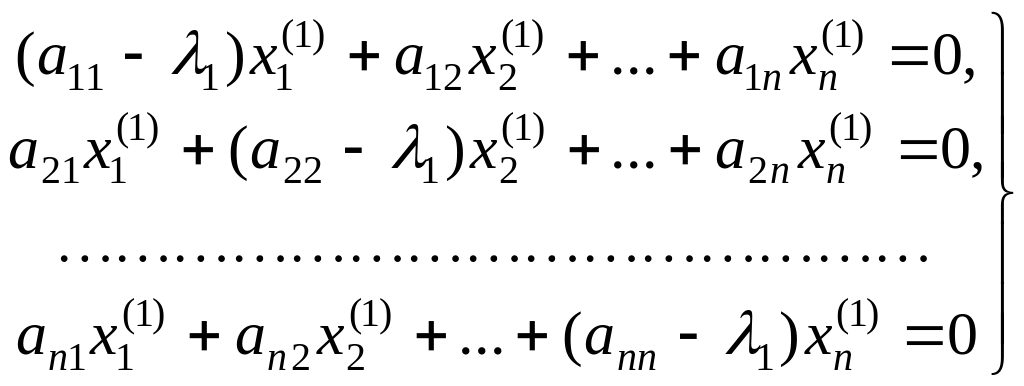
или

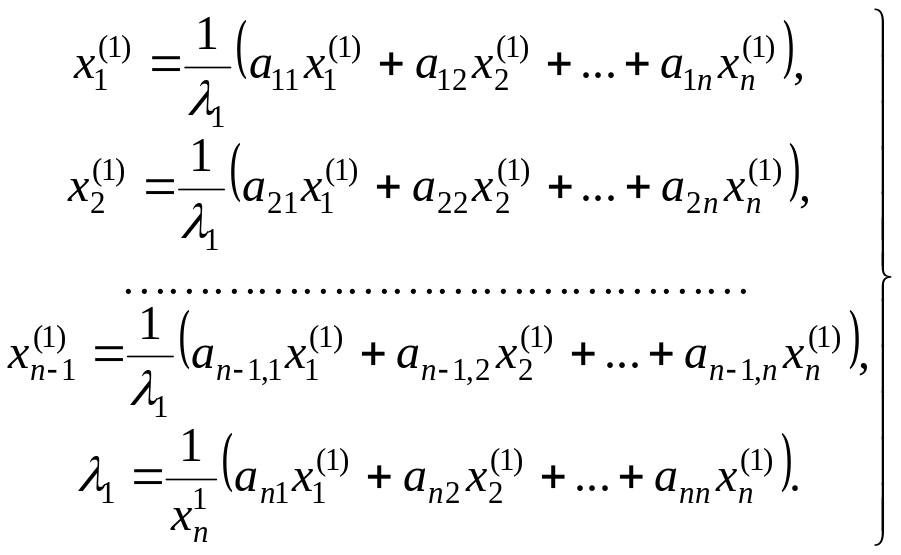(6.3)

Так как координаты собственных векторов определяются с точностью до множителя пропорциональности, то одна из них произвольна, например, за исключением особого случая, можно положить х_n⁽¹⁾ =1. Систему (6.3), вообще говоря, можно решить методом итерации, выбирая подходящие начальные значения x_i^(1,0) и λ₁⁽⁰⁾ и полагая

Можно также использовать процесс Зейделя. Таким образом, находятся первый корень характеристического уравнения (6.1)

(6.4)

и первый собственный вектор

.

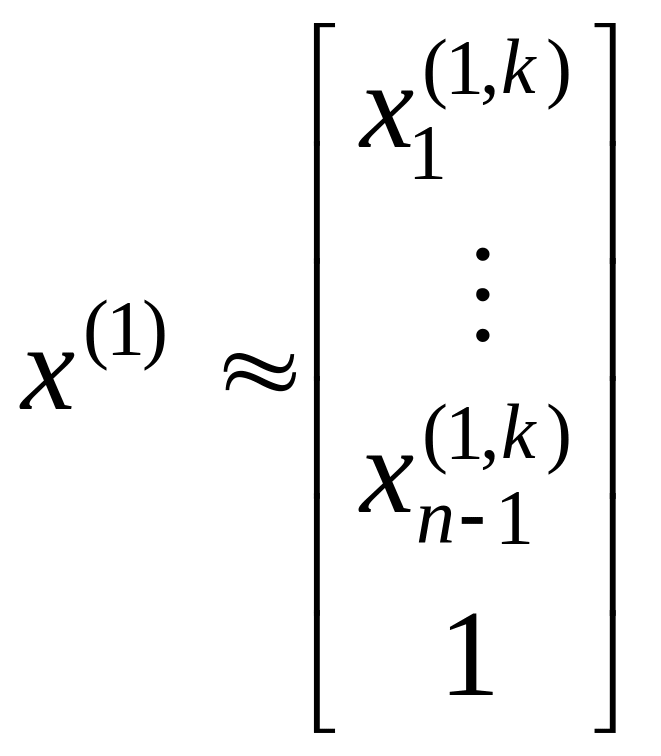Для определения второго корня λ₂ уравнения (6.1) и второго собственного вектора x⁽²⁾ напишем соответствующую систему уравнений

(6.5)

Из соотношения ортогональности

(6.6)

исключим одно из неизвестных х_j⁽²⁾, например х_n⁽²⁾. Тогда система (6.5) заменится эквивалентной системой

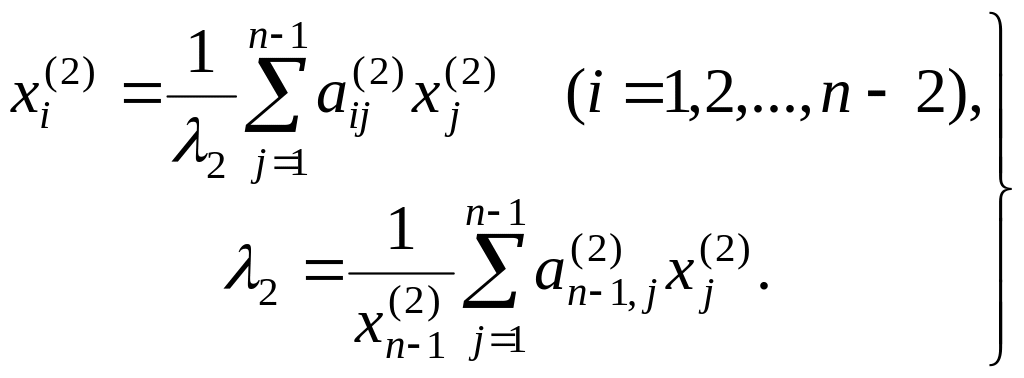(6.7)

Полагая х_n-1⁽²⁾=1, решаем систему (6.7) методом итерации. В результате будут найдены второй корень λ₂ характеристического уравнения (6.1) и собственный вектор x⁽²⁾, причем n-я координата этого вектора определяется из условия ортогональности (6.6). Аналогично отыскиваются остальные корни λ_j (j = 3,…, п) уравнения (6.1) и соответствующие им собственные векторы х^(j.⁾

7. Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней.

Если уравнение алгебраическое или трансцендентное достаточно сложно, то его корни сравнительно редко удается найти точно. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Поэтому важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Пусть дано уравнение

, (7.1)

где функция f(х) определена и непрерывна в некотором конечном или бесконечном интервале а < х < b.

В дальнейшем в некоторых случаях нам понадобится существование и непрерывность первой производной f ´(х) или даже второй производной f "(x), что будет оговорено в соответствующих местах.

Всякое значение ξ, обращающее функцию f(х) в нуль, т. е. такое, что

f(ξ)=0,

называется корнем уравнения (7.1) или корнем (нулем) функции f (х).

Мы будем предполагать, что уравнение (7.1) имеет лишь изолированные корни, т. е. для каждого корня уравнения (7.1) существует окрестность, не содержащая других корней этого уравнения.

Приближенное нахождение изолированных действительных корней уравнения (7.1) обычно складывается из двух этапов:

1. отделение корней, т. е. установление возможно тесных промежутков [а,b], в которых содержится один и только один корень уравнения (7.1);

2. уточнение приближенных корней, т. е. доведение их до заданной степени точности.

Для отделения корней полезна известная теорема из математического анализа:

рис. 3

Теорема 7.1. Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [α,β], т.е. f(α)f(β)<0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(х)=0, т. е. найдется хотя бы одно число ξ (α, β) такое, что f (ξ) = 0.

Корень ξ заведомо будет единственным, если производная f '(х) существует и сохраняет постоянный знак внутри интервала (α, β), т. е. если f '(х) > О (или f'(х)<0) при α<х<β (рис. 3).

Процесс отделения корней начинается с установления знаков функции f(x) в ряде промежуточных точек выбор которых учитывает особенности функции f(x). Если окажется, что , то в силу теоремы 1 в интервале (α_k,α_k+1) имеется корень уравнения f(x)=0. Нужно тем или иным способом убедиться, является ли этот корень единственным. Для отделения корней практически часто бывает достаточно провести процесс половинного деления, приближенно деля данный интервал (α,β) на две, четыре, восемь и т.д. равных частей и определяя знаки функции f(x) в точках делений.

Полезно помнить, что алгебраическое уравнение n-ой степени

имеет не более n действительных корней. Поэтому если для такого уравнения мы получили n перемен знаков, то все корни его отделены.

Пример 7.1. Отделить корни уравнения

(7.2)

Решение. Составляем приблизительную схему:

x	f(x)	x	f(x)
-∞ -3 -1 0	− − + +	1 3 +∞	− + +

Следовательно, уравнение (7.2) имеет три действительных корня, лежащих в интервалах (—3, —1), (0, 1) и (1, 3).

Если существует непрерывная производная f ´(х) и корни уравнения

f ´(x)=0

легко вычисляются, то процесс отделения корней уравнения (7.1) можно упорядочить. Для этого, очевидно, достаточно подсчитать лишь знаки функции f(х) в точках корней ее производной и в граничных точках х = а и х = b.

Графическое решение уравнений

Действительные корни уравнения приближенно можно определить как абсциссы точек пересечения графика функции y=f(x) с осью Ox. Если уравнение (7.1) не имеет близких между собой корней, то этим способом его корни легко отделяются. На практике часто бывает выгодно уравнение (7.1) заменить равносильным ему уравнением

(7.3)

где функции φ(х) и ψ(х) — более простые, чем функция f (х). Тогда, построив графики функций у=φ(x) и у = ψ(х), искомые корни получим как абсциссы точек пересечения этих графиков.

Пример 7.2. Графически решить уравнение

(7.4)

Решение. Запишем уравнение (7.4) в виде равенства .

Рис. 4

Отсюда ясно, что корни уравнения (7.4) могут быть найдены как абсциссы точек пересечения логарифмической кривой у = lg x и гиперболы у = 1/x. Построив эти кривые (рис. 4) на координатной бумаге, приближенно найдем единственный корень ξ≈2,3 уравнения (7.4).