4. Свойства матриц с действительными элементами.
Будем рассматривать матрицы A=[aij] элементы которых аij действительны; такие матрицы называются действительными или вещественными.
Пусть А = [aij] — действительная квадратная матрица порядка n. Так как ее характеристическое уравнение
det (A — λE) = 0
есть полином с действительными коэффициентами, то корни λ1, λ2, ..., λп характеристического уравнения, представляющие собой собственные значения матрицы А, в случае их комплексности попарно сопряжены, т. е. если λs есть собственное значение матрицы А, то сопряженное число λ*s также является собственным значением матрицы А и имеет ту же кратность.
Действительная матрица может не иметь действительных собственных значений. Однако в одном важном случае, когда элементы матрицы положительны, гарантируется существование хотя бы одного действительного собственного значения.
Теорема Перрона. Если все элементы квадратной матрицы положительны, то наибольшее по модулю собственное значение ее также положительно и является простым корнем характеристического уравнения матрицы, причем ему соответствует собственный вектор с положительными координатами.
Собственные векторы действительной матрицы А с различными собственными значениями в общем случае комплексные и не обладают свойством ортогональности. Однако, привлекая собственные векторы транспонированной матрицы А', можно получить так называемые соотношения биортогональности, которые для случая симметрической матрицы эквивалентны обычным соотношениям ортогональности.
Теорема 4.1. Если матрица А — действительная и собственные значения ее попарно различны, то существуют два базиса {хj} и {x´j} пространства Еп, состоящих соответственно из собственных векторов матрицы А и собственных векторов транспонированной матрицы А', удовлетворяющих следующим условиям биортонормировки:
Доказательство. Пусть λ1, λ2, ..., λп — собственные значения матрицы А. Так как матрица А — действительная, то, как мы знаем, собственные значения ее — попарно сопряженные, т. е. наряду с собственным значением λj, сопряженное число λj*;- также является собственным значением матрицы А. Обозначим через xj (j = 1, 2,..., п) соответствующие собственные векторы матрицы А, т. е.
Axj=λjxj (j=1, 2,...,n). (4.1)
Векторы { xj } образуют базис пространства Еп.
Так как определитель не изменяет своего значения при замене строк столбцами, то
det(A-λE)
и, следовательно, транспонированная матрица А' имеет те же собственные значения λj, что и матрица А. Пусть xj (j=1, 2, ...,n) — собственные векторы матрицы А', соответствующие сопряженным собственным значениям λj*, т. е.
(
j=1,
2, ..., n)
(4.2)
Векторы
также
образуют базис пространства Еп.
Базисы
{xj}
и
биортогональны,
а
именно:
(xj,
)=0
при j
≠ k.
(4.3)
Действительно, с одной стороны, имеем:
(Axj, )=(λjxj, )= λj(xj, ). (4.4)
С другой стороны, учитывая вещественность матрицы А, получаем:
(Axj
,
)=
(xj
,
)=
(xj
, λk*
)=
λk(xj
,
). (4.5)
Из равенств (4.4) и (4.5) выводим:
λ j(xj, )= λ k(xj, ). (4.6)
Taк как λj≠λk при j≠k, то из равенствa (4.6) вытекает равенство (4.3).
Покажем, что векторы {xj} и можно нормировать так, чтобы
(xj,
)=1
(j
= 1, 2, …,
n). (4.7)
В
самом
деле,
разлагая вектор
xj
по
векторам базиса {
},
будем иметь xj=
.
Отсюда, учитывая условие биортогональности (4.3), получим:
поэтому
.
Взяв
вместо векторов
векторы
,
получим
требуемую
нормировку (4.7), так как
Таким
образом, если собственные значения
действительной матрицы
A
различны,
то для
собственного
базиса {xj}
матрицы
A
всегда
можно найти собственный базис
транспонированной
мaтрицы
такой,
что
, (4.8)
где δjk — символ Кронекера.
Следствие. Если матрица A — действительная и симметрическая (A´=A), то можно положить: x´j=xj (j=1,2,…,n), где xj — нормированные собственные векторы матрицы A.
Тогда
(xj, xk)= δjk
Выведем еще так называемое билинейное разложение матрицы A.
Теоремa 4.2. Пусть A — квадратная действительная матрица и
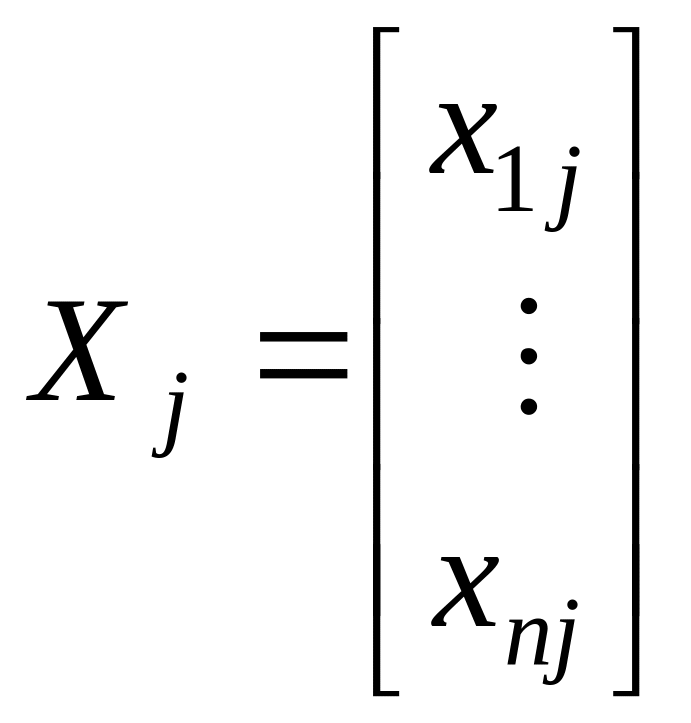
(j=1,2,…,n) — ee собственныe векторы, рассматривaeмые как матрицы – столбцы, и
X´k=[x´1k, …, x´nk]
(k = 1, 2, ..., n) — соответствующие coбcmвeнныe вeкmopы mpaнcnoнupoвaннoй матрицы A´, paccматриваемыe как матрицы-сmpoки, npuчем выnoлнeны условия 6uopmoнормировки (4.8):
(Xj,Xk´)=Xk´Xj=δjk . (4.9)
Тогда имеет место соотношение
A=λ1X1X´+1λ2X2X´2+...+λnXnXn´ , (4.10)
гдe λ1, λ2 ,..., λn—co6cmвенные значения матрицы A.
Доказательство. Рассмотрим матрицы
и
состоящие соответственно из столбцов Xj (j = 1,..., n) и строк Xk´ (k=l,…,n). В силу равенства (4.9) будем иметь:
, (4.11)
где E — единичная матрица. Taк как матрица X состоит из линейно независимых столбцов, то она — неособенная, т. е. detA≠0 и, следовательно, существует обратная матрица X -1. На основании равенства (4.11) имеем:
X -1=X´
Отсюда вытекает, что
XX´=E
и, таким образом, мы получаем вторые соотношения биортогональности
. (4.12)
Используя эти соотношения, имеем:
,
т.е.
E=X1X1´+X2X2´+…+XnXn´.
Умножая это равенство слева на матрицу A и учитывая, что
AXj=λjXj (j=1,2,…,n),
очевидно, получим равенство (4.10).