Варианты заданий

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. ;

10. ;

11. ;

12. 

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

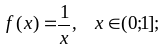
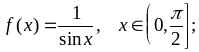
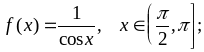
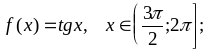
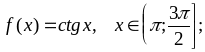
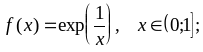
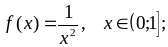
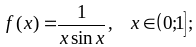
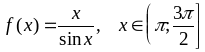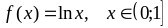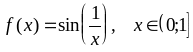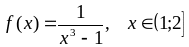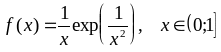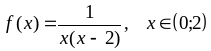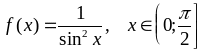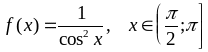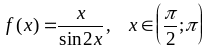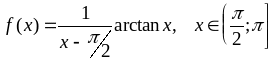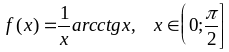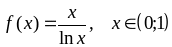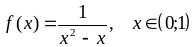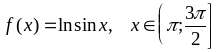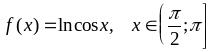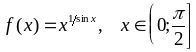Лабораторная работа №4 Численное решение задачи Коши для обыкновенных дифференциальных уравнений методами Рунге-Кутта

Цель работы. Решение обыкновенного дифференциального уравнения первого порядка методами Рунге-Кутта.

Теоретическая часть

Пусть требуется найти на отрезке решение дифференциального уравнения

(4.1)

Разобьем на отрезки . Последовательно будем получать приближения к значениям решения . Пусть значение уже найдено, тогда значение будем определять по следующей расчетной формуле

(4.2)

Этот метод называется методом Эйлера. Можно построить другой класс расчетных формул, к которому принадлежит метод Эйлера. Укажем сначала простейшие методы этого класса, получаемые из наглядных соображений. Пусть известно значение решения у(х) и требуется вычислить значение y(x+h). Рассмотрим равенство

(4.3)

При замене интеграла в правой части на величину hy'(x) погрешность имеет порядок , т. е.

у (х + h) = у (х) + hу' (х) + О(h²);

поскольку у'(х) = f(x, y(x)), то отсюда имеем

y(x + h) = y(x) + hf (х, у (х)) + О (h²).

Отбрасывая член порядка O(h²) и обозначая х =x_j, x+h =x_j+1, получим расчетную формулу Эйлера (4.2). Для получения более точной расчетной формулы нужно точнее аппроксимировать интеграл в правой части (4.3). Воспользовавшись формулой трапеций, получим

у (х + h) = у (х) + (у'(х) + у'(х + h)) + О (h³),

иначе,

y(x + h) = y(x) + (f(x,y (x))+f(y+h, y (x+h))) +О (h³). (4.4)

Соответствующая расчетная формула:

(4.5)

Обычно это уравнение неразрешимо явно относительно . Поэтому на практике чаще всего пользуются расчетными формулами

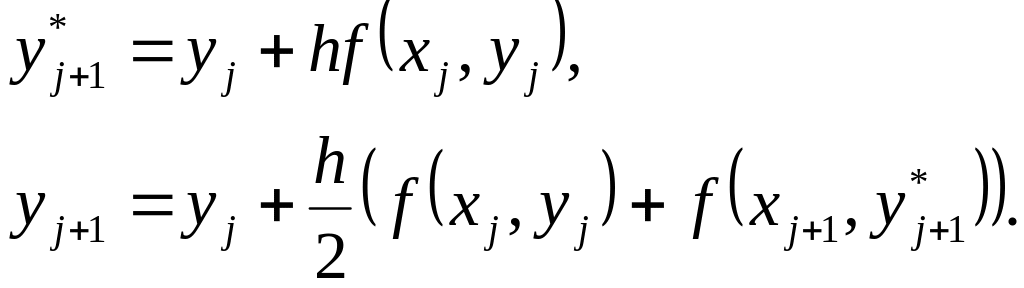(4.6)

Если интеграл в правой части (4.3) заменить по формуле прямоугольников, то можно построить другую пару расчетных формул с погрешностью на шаге того же порядка:

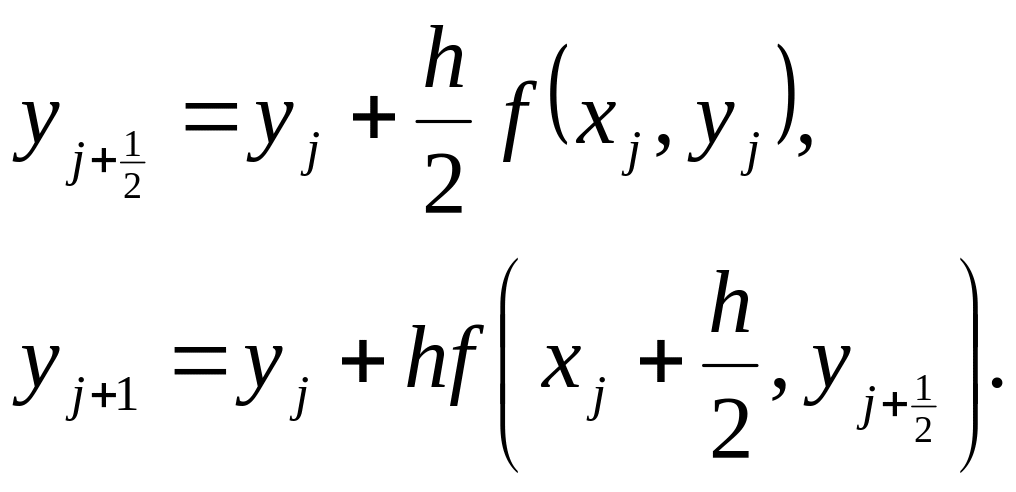(4.7)

Полученные методы относятся к семейству методов Рунге-Кутта.

Порядок выполнения лабораторной работы

1 Изучить теоретическую часть.

2 Составить программу решения дифференциального уравнения первого порядка по вычислительным схемам (4.2), (4.6) и (4.7). Отладить ее на модельной задаче.

3 Провести вычисления указанного варианта задачи.

4 Внести случайную погрешность в начальные данные и, проведя вычисления для измененных данных, сделать вывод об устойчивости.

5 Вывести результаты решения модельной задачи для различного числа узлов N в виде таблицы

где -значение приближенного решения в точке при шаге h, - точное значение решения в этой же точке.

6 Вывести результаты решения указанного варианта в виде

7 Провести анализ полученных результатов.