21. Преобразование Фурье.

Пусть f(x)—периодическая функция с периодом l — может быть разложена в ряд Фурье

(21.1)

причем

(21.2)

Рассмотрим значения этой функции на сетке из точек где l, N –целые, N – фиксировано, и обозначим Пусть - целое; тогда - целое и, следовательно,

(21.3)

в узлах сетки. Поэтому, если функция f(x) рассматривается лишь на сетке узлов х_l в соотношении (21.1) можно привести подобные члены

(21.4)

где

Если с самого начала была задана функция, определенная только на сетке, то на этой сетке ее можно также представить в форме (21.1). Действительно, такую функцию можно продолжить на всю прямую, доопределив ее между узлами сетки путем линейной интерполяции. Для непрерывной кусочно-дифференцируемой функции выполняется (21.2), и поэтому после приведения на сетке подобных членов получим (21.4). Определим скалярное произведение для функций на сетке:

Множитель 1/N введен для согласованности получаемых соотношений с непрерывным случаем: если f(x) и g(x) —непрерывные функции на [0, 1], то

при N→∞.

Функции при образуют ортонормированную систему относительно так введенного скалярного произведения. Действительно,

При суммируя геометрическую прогрессию, имеем

Поскольку то в итоге имеем

при (21.5)

Умножая (21.4) скалярно на , получим равенство

(21.6)

очевидно,

при и j фиксированном.

Однако это не означает, что

Посмотрим, почему это соотношение неверно. Пусть для простоты

где Из (21.4) получаем представление для коэффициентов

Таким образом, правая часть этого неверного приближенного равенства есть

Она совпадает с f(x) в точках x_l, но далека от нее вне этих точек.

Заменой переменной суммирования в определении убеждаемся, что , если где k – целое. Воспользовавшись равенством (21.3), перепишем (21.4) в виде

(21.7)

Если f(x) – достаточно гладкая, то величины с ростом j убывают быстро, и поэтому, при малых q; кроме того, тогда величины и малы при больших q. В итоге есть основание надеяться на справедливость приближенного равенства

(21.8)

во всех точках х.

Это приближенное равенство обращается в равенство в точках сетки. Способ аппроксимации функции правой частью (21.8) носит название тригонометрической интерполяции. Соотношение (21.7) называют конечным или дискретным рядом Фурье, а коэффициенты A_q — дискретными коэффициентами Фурье.

Быстрое преобразование Фурье. Осуществление прямого, и обратного дискретных преобразований Фурье

является составной частью решения многих задач. Непосредственное осуществление этих преобразований по формулам (21.4), (21.6) требует O(N²) арифметических операций. Рассмотрим вопрос о возможности сокращения этого числа операций; для определенности речь пойдет о вычислении коэффициентов A_q по заданным значениям функции. Идея построения алгоритмов быстрого преобразования Фурье опирается на то, что при N составном в слагаемых правой части (21.6) можно выделить группы, которые входят в выражения различных коэффициентов A_q.

Рассмотрим сначала случай Представим q, j, лежащие в пределах в виде где Имеем цепочку соотношений

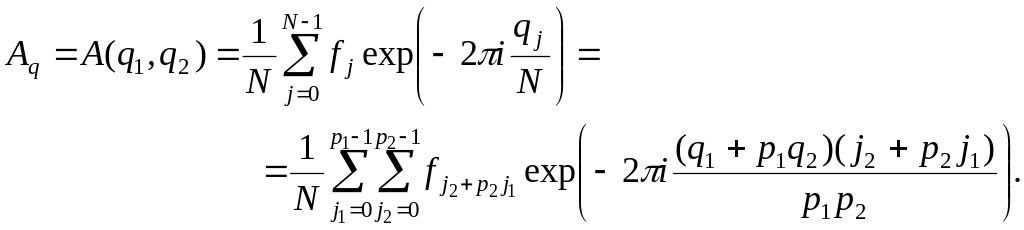
Из равенства

и предыдущего соотношения получим

где

Непосредственное вычисление всех требует арифметических операций, а последующее вычисление требует еще операций. Следовательно, при общее число операций будет Точно так же при строится алгоритм вычисления совокупности значений , для которого общее число операций не превосходит здесь C – абсолютная постоянная. Выпишем соответствующие расчетные формулы для наиболее употребительного случая Представим числа q, j в виде

где Величину можно представить в виде

где s – целое, равное сумме всех слагаемых

у которых Очевидно,

Поэтому

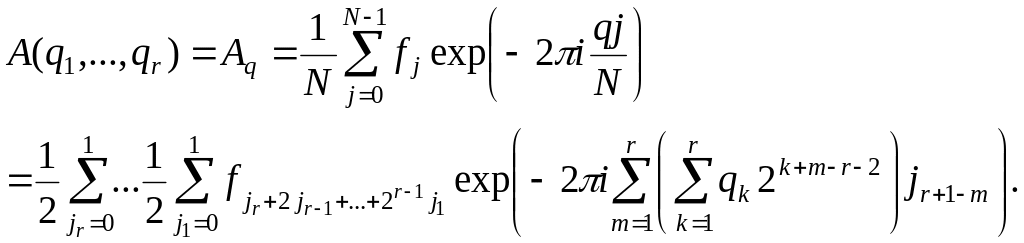
После перегруппировки слагаемых имеем

Это соотношение можно записать в виде последовательности реккурентных соотношений

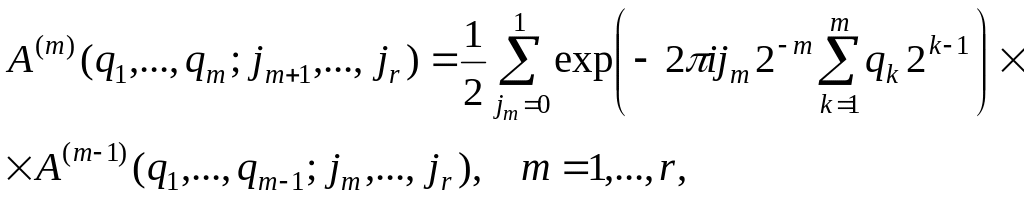
где