18. Численные методы решения обыкновенных дифференциальных уравнений.

Метод последовательных приближений. Изложим этот метод применительно к дифференциальному уравнению первого порядка

(18.1)

с начальным условием

(18.2)

Предполагается, что в некоторой окрестности точки М₀ (x₀, у₀) уравнение (18.1) удовлетворяет условиям теоремы существования и единственности решения.

Будем строить, искомое решение у=у(х) для значений х≥х₀ Случай х≤х₀ вполне аналогичен. Интегрируя правую и левую части уравнения (18.1) в пределах от х₀ до х, получим

или, в силу начального условия (18.2), будем иметь

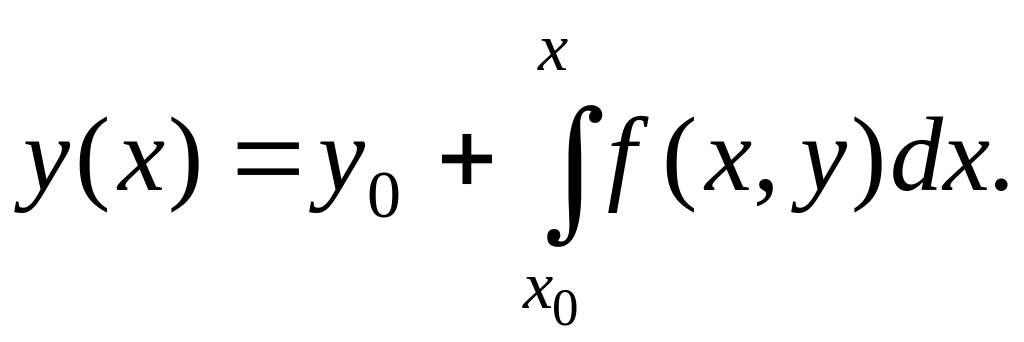(18.3)

Так как искомая функция у=у(х) находятся под знаком интеграла, то уравнение (18.3) является интегральным. Очевидно, решение интегрального уравнения (18.3) удовлетворяет дифференциальному уравнению (18.1) и начальному условию (18.2).

Для нахождения этого решения применим метод последовательных приближений. Заменяя в равенстве (18.3) неизвестную функцию у данным значением у₀, получим первое приближение

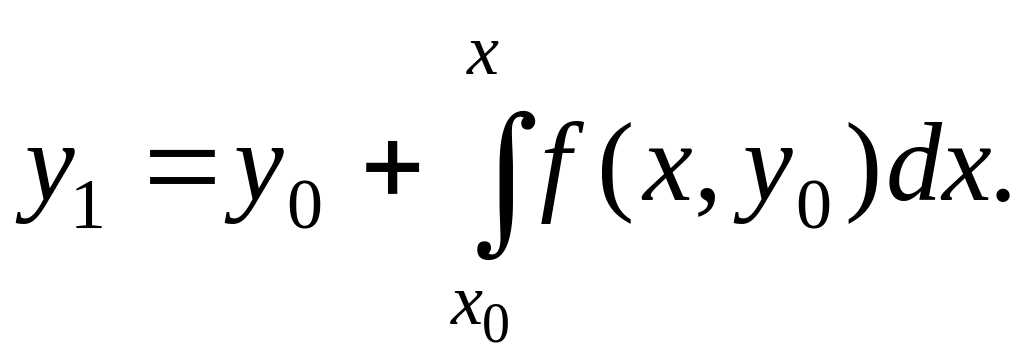
Далее, подставив в равенстве (18.3) вместо неизвестной функции у найденную функцию y₁, будем иметь второе приближение

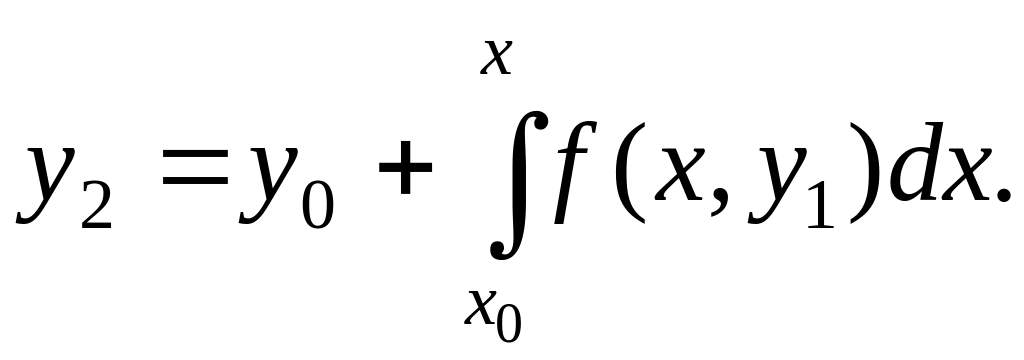
Вообще, все дальнейшие приближения строятся по формуле

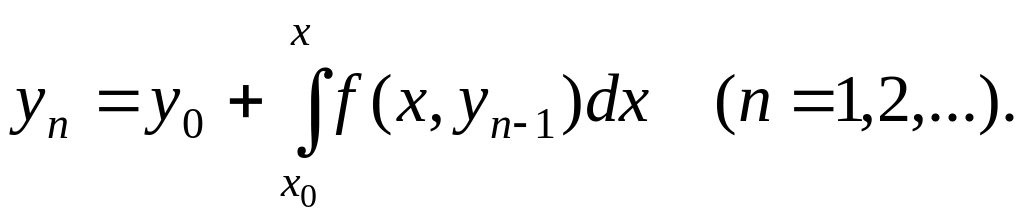(18.4)

Геометрически последовательные приближения представляют собой кривые у_п = у_п(х) (n=1, 2, ...), проходящие через общую точку M₀(x₀,y₀).

Замечание. При методе последовательных приближений в качестве начального приближения у₀, вообще говоря, можно выбирать любую функцию, достаточно близкую к точному решению у.

Например, иногда выгодно в качестве у₀ брать конечный отрезок ряда Тейлора искомого решения.

Заметим, что при пользовании методом последовательных приближений аналитичность правой части дифференциального уравнения не обязательна, поэтому метод этот можно применять и в тех случаях, когда разложение решения дифференциального уравнения в степенной ряд невозможно.

Пример 18.1. Методом последовательных приближений найти приближенное решение дифференциального уравнения

удовлетворяющее начальному условию

у(0)=1.

Решение. В качестве начального приближения возьмем у₀ (х) = 1. Так как

то будем иметь

Аналогично

Подобным же образом получим

и т.д.

Разложение решения в ряд Тейлора.

Одним из старейших методов решения дифференциальных уравнений является метод разложения в ряд Тейлора.

Пусть требуется найти на отрезке решение дифференциального уравнения (18.1) при начальном условии (18.2). f(x,y) аналитична в точке Дифференцируя (18.1) по x, имеем соотношения

Подставляя и , получаем последовательно значения

Таким образом, можно написать приближенное равенство

(18.5)

Если больше радиуса сходимости ряда

то погрешность (18.5) не стремится к нулю при n→∞. Иногда целесообразно поступить следующим образом.

Разобьем на отрезки

последовательно получаем приближения y_j к значениям решения

по следующему правилу: пусть значение y_j уже найдено, вычисляем значения в точке x_j производных решения исходного дифференциального уравнения, проходящего через точку ; на отрезке полагаем

(18.6)

и, соответственно полагаем

(18.7)

Методы Рунге-Кутта и Эйлера. В частном случае п = 1 расчетная формула (18.6) имеет вид

(18.8)

Этот метод называется методом Эйлера. Можно построить другой класс расчетных формул, к которому принадлежит метод Эйлера. Укажем сначала простейшие методы этого класса, получаемые из наглядных соображений. Пусть известно значение решения у(х) и требуется вычислить значение y(x+h). Рассмотрим равенство

(18.9)

При замене интеграла в правой части на величину погрешность имеет порядок , т.е.

поскольку то отсюда имеем

Отбрасывая член порядка и обозначая получим расчетную формулу Эйлера (18.8). Для получения более точной расчетной формулы нужно точнее аппроксимировать интеграл в правой части (18.9). Воспользовавшись формулой трапеций, получим

иначе,

(18.10)

Соответствующая расчетная формула:

(18.11)

Обычно это уравнение неразрешимо явно относительно . Поэтому произведем дальнейшее преобразование алгоритма. Заменим в правой части (18.10) на некоторую величину

(18.12)

тогда правая часть изменится на величину

где находится между и вследствие предположения (18.12) эта величина имеет порядок Таким образом, при условии (18.12)

условию (18.12) удовлетворяет результат вычислений по расчетной формуле Эйлера

Последние соотношения определяют пару расчетных формул

(18.13)

Построим другую пару формул с погрешностью на шаге такого же порядка. Интеграл в правой части (18.9) заменим по формуле прямоугольников:

или, все равно, что

Если

то, как и в предшествующем случае, имеем

В качестве можно взять результат вычислений по формуле Эйлера с шагом :

Этим соотношениям соответствует пара расчетных формул

(18.14)

Полученные методы относятся к семейству методов Рунге-Кутта, имеющих следующий вид. В процессе вычислений фиксированы некоторые числа

последовательно получаем

и полагаем