14. Приближение функций в среднем квадратичном. Ортогональные полиномы.

Метод наименьших квадратов. При точечном квадратичном аппроксимировании за меру отклонения полинома

(14.1)

от данной функции y=f(x) на множестве точек х₀, x₁ ... , х_п принимают величину

(14.2)

называемую квадратичным отклонением (способ наименьших квадратов).

Для построения аппрксимирующего полинома требуется подобрать коэффициенты так, чтобы величина S была наименьшей. Предполагаем, что . В случае m=n коэффициенты (j=0,1,2,…,m) можно определить из системы уравнений

при i=0,1,2,,…,m, (14.3)

причем S = 0, и приходим к разобранной выше проблеме интерполирования функций. При т≤п система (14.3), вообще говоря, несовместна. Кроме того, следует иметь в виду, что во многих случаях значения функции f(x) определяются экспериментально и содержат ошибки, поэтому сама постановка вопроса о точном решении системы (14.3) теряет смысл.

Для решения нашей задачи аппроксимирования воспользуемся общим приемом дифференциального исчисления. А именно, найдем частные производные от величины

где у_i=f(х_i), по всем переменным а₀, а₁ ... , а_т.

Приравнивая эти частные производные нулю, получим для определения неизвестных а₀, а₁, ... , а_т систему m+1 уравнений с m+1 неизвестными:

(14.4)

Разложение функции в ряд по ортогональным многочленам.

Если степень аппроксимирующего полинома больше трех, то вычисление по способу наименьших квадратов становится очень громоздким. Поэтому был создан новый метод построения аппроксимирующего полинома. В основе этого нового метода лежит понятие об ортогональных функциях.

Определение. Функции φ(х) и ψ(х) называются ортогональными на множестве точек Х={х₀, х₁, ... , х_п}, если

Система функций {φ_i(x)} называется ортогональной на данном множестве X, если функции системы попарно ортогональны между собой на множестве X.

Очевидно, функция φ(x), обращающаяся в нуль в точках х₀, х₁, ... , х_п, ортогональна на этом множестве точек к любой другой функции. В дальнейшем предположим, что не все точки x_i (i = 0,1,..., n) являются нулями рассматриваемых функций φ_k (х), т.е.

Пусть

(14.5)

- заданная система ортогональных на множестве {х₀, х₁, ... , х_п} полиномов, т.е.

при (14.6)

причем индексы полиномов соответствуют их степеням. Предположим, что

(14.7)

Так как полиномы P_j(x) (j=0, 1,2, ... , т) линейно независимы, то произвольный полином Q_m(х) степени т можно представить в виде линейной комбинации полиномов из системы (14.5), т. е.

(14.8)

Это представление называется разложением полинома Q_m(x) по системе (14.5).

Можно дать явные формулы для коэффициентов b_о, b₁,..., b_т. Умножим тождество (14.8) на полином P_k(x) (k≤m) и просуммируем полученное равенство по системе точек х₀, х₁, ... ,х_п. Тогда

Отсюда, учитывая условия ортогональности (14.6), находим

и, следовательно,

Вернемся к задаче аппроксимирования заданной функции у=f(х) на множестве точек х₀, х₁,, ... ,х_п полиномом данной степени т (т≤п). Искомый полином Q_m (x), для которого квадратичное отклонение

будем искать в форме (14.8). Отсюда

(14.9)

Преобразуем выражение (14.9). Возводя в квадрат выражение, стоящее в квадратных скобках, получим

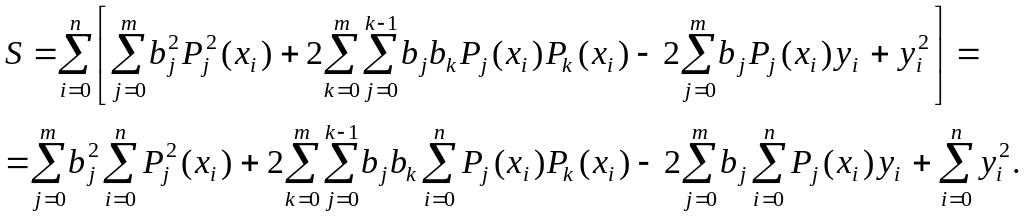(14.10)

Но в силу условий ортогональности (14.6)

Поэтому, вводя обозначение

и используя обозначение (14.7), будем иметь

Выражение, стоящее в круглых скобках под знаком первой сумма, дополним до полного квадрата:

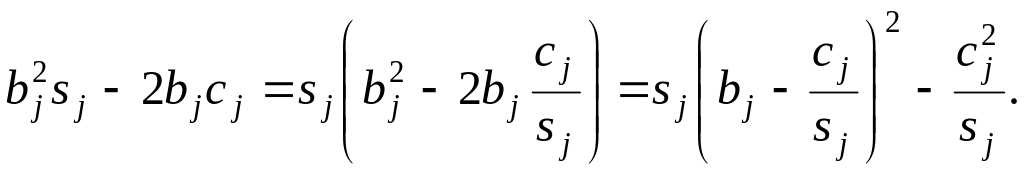
Тогда

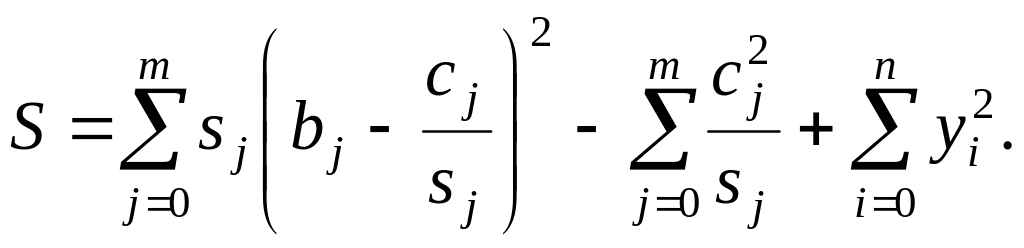(14.11)

В выражении (14.11) коэффициенты b₀, b₁ ... ,b_т нужно подобрать так, чтобы квадратичное отклонение S было минимальным.

Заметим, что последние две суммы в формуле (14.11) не зависят от выбора коэффициентов b_о, b₁, ,.. , b_т, Поэтому минимальное значение S достигается для тех коэффициентов b_j, для которых является минимальной сумма

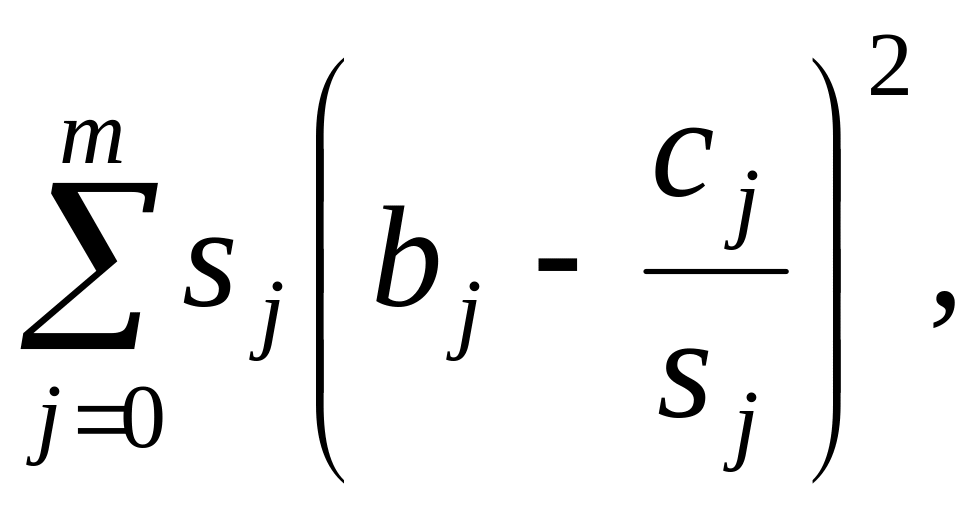
что, очевидно, будет при

(14.12)

Отсюда искомый аппроксимирующий полином имеет вид

причем квадратичное отклонение S этого полинома от данной функции y=f(x) на множестве точек , как вытекает из формулы (14.11), дается формулой