ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кудряшова Н.Ю.

Численные методы

Учебное пособие

ПЕНЗА

2006

УДК 517.

Приводится подробный конспект лекций по дисциплине «Численные методы» для студентов технических специальностей. Рассматриваются такие основные разделы, как численные методы линейной алгебры; приближенные методы решения нелинейных уравнений и систем уравнений; приближение функций; численное дифференцирование и интегрирование; численные методы решения дифференциальных уравнений; быстрое преобразование Фурье; решение основной задачи линейного программирования.

Составлено достаточное количество задач по дисциплине. Предложены типовые лабораторные работы с указаниями по их выполнению. Представлены общие требования к оформлению отчетов о выполнении лабораторных работ и варианты заданий.

Учебное пособие подготовлено на кафедре «Высшая и прикладная математика» и предназначено, в первую очередь, для студентов специальности 090106 – «Информационная безопасность телекоммуникационных систем», а также для студентов других технических специальностей, изучающих курс «Численные методы».

Библиография 9 назв.

Составитель: Кудряшова Н.Ю.

Рецензенты:

А.М. Данилов, д.т.н., профессор, заведующий кафедрой «Высшая математика» Пензенского государственного университета архитектуры и строительства;

В.И. Паньженский, профессор, декан физико-математического факультета Пензенского государственного педагогического университета.

Конспект лекций

1. Погрешности вычислений. Устойчивость алгоритма. Норма матриц. Матричные ряды.

Погрешность результата численного решения задачи. Устойчивость алгоритма.

Отклонение истинного решения от приближенного назовем погрешностью.

Решение задач всегда имеют погрешность, связанную со следующими причинами:

1) созданием математической модели (любая модель имеет свою степень точности);

2) получением исходных данных (т.к. являются "результатом измерений", следовательно, возникают измерительные погрешности);

3)использованием вычислительной техники (ошибки округления, возникающие из-за ограниченной разрядной сетки и ошибки, связанные с самими методами).

На рис. 1 и 2 показаны составляющие неустранимой и полной погрешности.

Неустранимая погрешность

Полная погрешность

погрешности исходных данных

погрешности математической модели

неустранимая погрешность

погрешность метода

вычислительная погрешность

.

рис.1 рис.2

Неустранимую погрешность и погрешность метода необходимо контролировать, чтобы не осуществлять расчеты с избыточной точностью.

Характеристиками точности результата решения задачи являются абсолютная и относительная погрешности. Для технических задач 10 % - хорошая точность.

Определение. Если х - точное значение некоторого числа, х^* - приближенное, то абсолютной погрешностью приближения х^* назовем величину: Δx*≥|x-x*|, т.е. точное значение числа х заключено в границах x*-Δx*≤x≤x*+Δx*.

Определение. Отношение абсолютной погрешности к абсолютному значению приближенной величины есть относительная погрешность (т.е. доля истинного значения):δx*=Δx*/|x*|, при условии, что |x*|≠0.

Алгоритм называется устойчивым, если небольшому изменению начальных данных соответствует столь же небольшое изменение конечного результата.

Норма матриц. Матричные ряды.

Под абсолютной величиной (модулем) матрицы A = [a_ij] понимается матрица

Под нормой матрицы A = [a_ij] понимается действительное число ||А||, удовлетворяющее условиям:

a) ||А||>0, причем ||А||=0 тогда и только тогда, когда A = 0;

6) ||А|| =|a|∙||А|| (a — число) и, в частности, ||-А|| =||А||;

в) ||А+В ||<||А||+||В||;

г) ||АB||<||А||∙||В||.

(A и В— матрицы, для которых соответствующие операции имеют смысл). В частности, для квадратной матрицы имеем ||А^p|| < ||А||^p , где р—натуральное число.

Отметим еще одно важное неравенство между нормами матриц А и В одинакового типа. Применяя условие в), будем иметь:

||В|| = ||А+(В-А)||<||А||+||В-А||.

Отсюда

||А-В|| = ||В-А|| > ||В||-||А||.

Аналогично

||А-В|| > ||А||-||В||.

Следовательно,

||А-В|| > |||В||-||А|||.

Назовем норму канонической, если дополнительно выполнены условия:

д) если А = [а_ij], то |a_ij| < ||А||,

причем для скалярной матрицы A = [a₁₁] имеем ||А|| = |a₁₁|;

e) из неравенства |А| < |В| (A и B — матрицы) следует нepaвенство

||А|| < ||В||.

B частности, ||А|| = || | А | ||.

B дальнейшем для матрицы А = [a_ij] произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы:

1. ||А||_m = |a_ij| (m - норма);

2. ||А||_l = |a_ij| (l - норма);

3. ||А||_k = (k - норма).

В частности, для вектора

эти нормы имеют следующие значения:

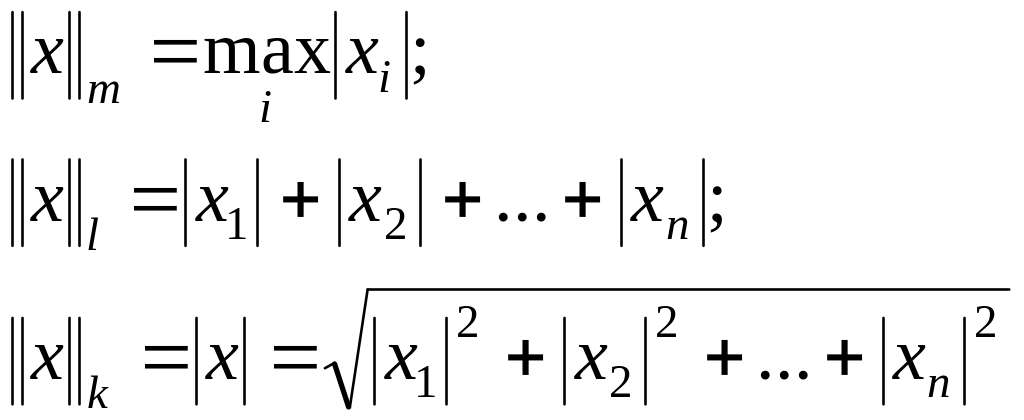
(абсолютная величина вектора). Если компоненты вектора действительны, то имеем просто:

Пусть имеется последовательность матриц

A_k=[a_ij^(k)] (k = 1, 2, …) (1.1)

одного и того же типа m×n (i = 1, 2, ... , m; j = 1, 2, ... , n). Под пределом последовательности матриц A_k понимается матрица

(1.2)

Последовательность матриц, имеющая предел, называется сходящейся.

Лемма 1.1. Для сходимости последовательности матриц A_k (k=1, 2, . . .) к матрице A нeoбходимо и достаточно, чmoбы

при , (1.3)

гдe ||А|| — любая каноническая норма матрицы A. При этом

Действительно, если A_k→A=[a_ij], то |a_ij-a_ij^(k)|<ε при k>N (ε). Отсюда

|A-A_k|<εI

где I — матрица типа m ×n, все элементы которой равны единице. B силу свойств ноpмы имеем:

|A-A_k|≤ε||I|| при k>N(ε),

следовательно,

(1.4)

Обратно, пусть выполнено условие (1.3). Тогда при k>N(ε) имеем:

|a_ij-a_ij^(k)|≤||A-A_k||<ε

и, следовательно,

т.е.

Кроме того, если A_k→A, то имеем:

| ||A||-||A_k|| |≤||A-A_k||→0 при k→∞.

Поэтому

.

Следствие. Последовательность _{Ak →0 при} k→∞ _{тогда и только тогда, когда .}

Пользуясь понятием предела матрицы, можно ввести в рассмотрение матричные ряды

, (1.5)

где А_к — матрицы одного и того же типа.

Если предел (1.5) существует, то матричный ряд называется сходящимся, и матрица, полученная в пределе, называется суммой этого ряда. Если предела (1.5) не существует, то матричный ряд называется расходящимся и ему не приписывается никакой суммы.

Необходимое условие сходимости матричного ряда.

Теорема 1.1. Если матричный ряд (1.5) сходится, то .

Доказательство. Пусть . Если ряд (1.5) сходится, то существует конечный предел . Имеем: A_k=S_k-S_k-1, откуда

Матричный ряд (1.5) называется абсолютно сходящимся, если сходится ряд .

Теорема 1.2. Если ||A|| —любая каноническая норма, а числовой ряд сходится, то матричный ряд (1.5) также сходится и притом абсолютно.

Теорема 1.3. Для того чтобы A^m→0, необходимо а достаточно, чтобы все собственные значения матрицы А были по модулю меньше единицы.