Теория нитяного дальномера.

Рассмотрим частный случай – местность ровная,  = 0. Из подобия треугольников со сторонами m и n (рисунок 12) можно записать.

1 - луч, проходящий через точку пересечения нитей (визирная¹¹⁾ ось);

2 - лучи, проходящие через верхнюю и нижнюю дальномерные нити;

3 - дальномерные нити;

4 - рейка.

Рисунок 12 - Схема определения дальномерного расстояния D.

11) Слово «Визировать» означает «наблюдать».

(12)

где f – фокусное расстояние зрительной трубы теодолита;

m – расстояние между дальномерными нитями сетки нитей зрительной трубы теодолита;

n - количество делений на нивелирной рейке между лучами, проходящими через дальномерные нити.

Обозначим - величину, постоянную для теодолита, через  (коэффициент дальномера); формула (12) примет вид:

, (13)

тогда D из рисунка 12 вычисляется по формуле:

, (14)

В выпускаемых в настоящее время теодолитах с внутренней фокусировкой зрительной трубы величина мала, около 1 см, ею при определении расстояний нитяным дальномером теодолита можно пренебречь. В этом случае формула (14) примет вид:

, (15)

Рассмотрим теперь общий случай наклонной местности (рис.13).

Принимая угол и наведение визирной оси трубы теодолита на отсчет по рейке, равный высоте инструмента i, можно записать:

(16)

Горизонтальное проложение d из рисунка 13 равно:

, (17)

1-луч, проходящий через точку пересечения нитей (визирная ось);

2-лучи, проходящие через верхнюю и нижнюю дальномерные нити

3-линия горизонта;

Рисунок 13 – Схема, иллюстрирующая определение d и h' (частный

случай – наведение визирной оси на высоту инструмента i)

Подставив значение D из формулы (16) получим:

или

, (18)

Превышение h из рисунка 13 равно:

¹²⁾, (19)

12) - превышение, определяемое для случая наведения визирной оси на высоту инструмента, отмеченную на рейке.

подставив значение d из формулы (18) получим:

или

,

или

Из тригонометрии известно, что:

,

тогда

, (20)

В случае, когда навести среднюю нить сетки нитей теодолита на высоту инструмента по рейке невозможно из-за наличия препятствия, она наводится на любое видимое дециметровое деление рейки. Тогда превышение определяют по формуле, вытекающей из рисунка 14:

(21)

Подставим значение h из формулы (20), тогда формула (21) примет общий вид:

, (22)

Отметку реечной точки при тахеометрической съемке вычисляют по формуле:

, (23)

где Н_р – отметка реечной точки;

Н_ст – отметка станции (полюс в полярной системе координат);

h – превышение со своим знаком.

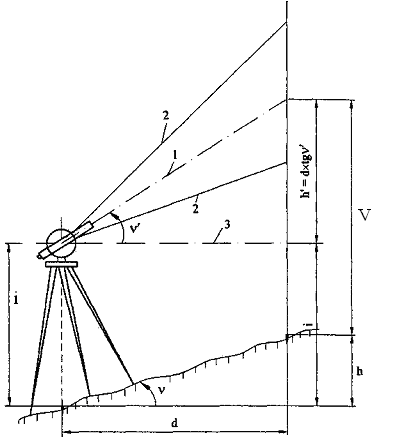
1-визирная ось;

2-лучи, проходящие через дальномерные нити;

3-линия горизонта.

Рисунок 14 – Схема, иллюстрирующая определение превышения для

общего случая – наведение визирной оси трубы на

произвольный отсчет V по рейке

Все приведенные выше формулы содержат значения вертикального угла . Определим связь между отсчетами по вертикальному кругу теодолита КЛ, КП и вертикальным углом .

Теория вертикального круга.

Вертикальный угол  находится в вертикальной плоскости и отсчитывается от линии горизонта. Если угол  находится над горизонтом, то ему присваивается знак плюс, под горизонтом – минус (рисунок 15).

Цель

+ Линия горизонта

-

Цель

Рисунок 15 – Схема вертикального угла.

Вертикальный круг теодолита (рисунок 16) состоит из:

1. лимба, вращающегося вместе с трубой, визирная ось которой определяет направление на наблюдаемую точку;

2. алидады – неподвижной при измерении, нулевой диаметр алидады выражает линию горизонта.

Из-за атмосферного воздействия, прежде всего перепада температуры воздуха, а также других причин (вибрации, ударов), нулевые диаметры лимба и алидады не сохраняют неизменного положения, что проиллюстрировано на рисунке 16.

КП

б)

КЛ

а)

1 – лимб;

2 – алидада;

3 – линия горизонта;

4-нулевой диаметр алидады;

5-нулевой диаметр лимба.

Рисунок 16 – Схема вертикального круга теодолита 2Т30.

Вертикальный угол, определяемый дугой между нулевыми штрихами лимба и алидады(отсчеты по вертикальному кругу «КЛ», «КП»), выражает не

действительное значение , а искаженное на величину +. Величину + называют местом нуля вертикального круга и обозначают индексом МО. Т.е.:

МО = +, (24)

Для того, чтобы получить действительное значение угла , нужно из отсчетов по вертикальному кругу исключить значение МО. Определение значения места нуля (МО) теодолита выполняют при двух его положениях, при вертикальном круге слева (КЛ) и справа (КП) от окуляра зрительной трубы. Разметка вертикального круга теодолита 2Т30 и два его положения КП и КЛ при направлении на одну визирную цель приведены на рисунке 16.

Из рисунка16(а):

 = КЛ – МО, (25)

Из рисунка 16 (б):

 = МО – КП, (26)

Вычитая из (25) (26) получим:

2МО = КЛ + КП,

(27)

Сложив (25) и (26) получим:

2 = КЛ – КП,

(28)

При тахеометрической съемке теодолитом 2Т30 вертикальный угол  вычисляют по формуле (25) через место нуля вертикального круга, считая значение его в пределе времени работы на одной станции постоянным.