Информационная энтропия

В качестве меры неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии в теории информации является основным.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

(11)

Здесь — вероятность i-го выходного значения и . Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями p и q = (1  p), выражение для энтропии примет следующий вид:

В нашем случае появление четырех единиц или нулей в исходной последовательности приводят к появлению постоянной составляющей на зажимах передатчика. Однако изолирующий трансформатор не обеспечивает прохождения через себя постоянного электрического тока, что может привести к возникновению потерь в линии связи, то есть к неопределенности. Соответственно, чем больше таких 4-битовых слов присутствует в исходной последовательности, тем больше величина информационной энтропии и наоборот. Именно по этой причине энтропия рассчитывается для 4-битовых слов, состоящих только из 0 или 1.

Вычисление энтропии сводится к нахождению вероятности появления, интересующего нас 4-битового слова, в данном случае 0000 или 1111. Поэтому исходная последовательность разбивается на слова, состоящих из 4 бит, и определяется количество появления каждого слова в исходной битовой последовательности. В нашем случае количество неповторяющихся слов ограничено и равно . Полученные величины нормируются и определяются их вероятности. По формуле (11) рассчитывается энтропия. В качестве параметров энтропии выбираются вероятности появления 4-битовых слов, состоящих только из 0, а также только из 1.

В результате всех преобразований (рис. 8), полученная кодовая последовательность кодируется в электрический, электромагнитный или световой сигнал, в зависимости от среды передачи данных. Начиная с этого момента, мы уже имеем дело не с битовой последовательностью, а с последовательностью импульсов, обладающих характеристиками: длительность импульса, амплитуда импульса… Однако среда передачи данных не является идеальной и вносит свои искажения в передаваемый сигнал, и, следовательно, искажает форму прямоугольного импульса. Причину возникновения искажения сигнала поможет узнать математический анализ Фурье.

Ряды Фурье

В начале XIX в. французский математик Жан-Батист Фурье (Jean-Baptiste Fourier) доказал, что любая периодическая функция x(t) с периодом Т может быть разложена в ряд (возможно, бесконечный), состоящий из сумм синусов и косинусов, имеющих различные частоты и амплитуды. Подобное разложение называется рядом Фурье. Разложенная в ряд Фурье функция может быть восстановлена по элементам этого ряда, то есть если период Т и амплитуды гармоник известны, то исходная функция может быть восстановлена с помощью суммы этих гармонических составляющих.

Информационный сигнал, имеющий конечную длительность (все информационные сигналы имеют конечную длительность), может быть разложен в ряд Фурье, если представить, что весь сигнал бесконечно повторяется снова и снова (то есть интервал от Т до 2Т полностью повторяет интервал от 0 до Т, и т. д.).

Математически, сигнал, повторяющийся через определенный период Т можно описать следующим выражением , . В связи с тем, что реальные сигналы (функции) имеют период отличный от 2π, то более подходящим в аналитических расчетах является использование угловой частоты , измеряемой в радианах в секунду. Смысл этого выражения проиллюстрирован на рис. 9.

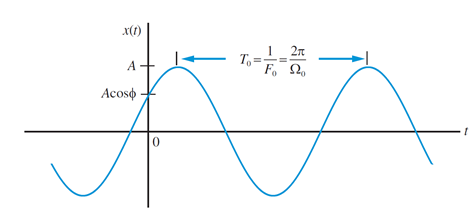
Рис. 9. Косинусоидальный сигнал с параметрами

Теорема Фурье утверждает, что любой периодический сигнал x(t) можно разложить на бесконечные последовательности синусоидальных и косинусоидальных функций:

(12)

или можно записать выражение (12), учитывая, что период функции не равен 2:

(13)

Коэффициенты и можно определить, решив следующие выражения:

(14)

(15)

(16)

Пределы интегрирования могут также находиться в диапазоне . Любая функция, разлагаемая в ряд Фурье, должна отвечать условиям Дирихле: быть ограниченной, кусочно-непрерывной и имеющей на протяжении периода конечное число экстремумов.

Из формулы (13) можно увидеть, что функция x(t) содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами (n = 1, 2, …), кратными основной частоте последовательности. Можно показать, что имеет место равенство

(17)

Если записать коэффициенты ряда Фурье в виде

где амплитуда гармоники —

, (18)

фазовая составляющая гармоники —

, (19)

то получим эквивалентную форму ряда Фурье:

(20)

Амплитудный спектр можно изобразить графически вертикальными отрезками длиной A_n: по оси абсцисс отмечаем значения частот , 2, 3, …, k, …, по оси ординат — соответствующие значения этим частотам амплитуды A₁, A₂, A₃, …, A_k, … . При этом считаем, что постоянной составляющей периодического колебания A0 соответствует частота  = 0.

Рис. 10. Спектр амплитуд

Аналогично изображается фазовый спектр.

Поскольку периодическая функция представляется бесконечной суммой гармоник с кратными частотами, то ее спектр носит дискретный характер.

Для многих практических приложений достаточно знать лишь амплитудный спектр функции. Изучая амплитудный спектр ряда Фурье периодического колебания, легко найти те значения частот, которым соответствуют большие значения A_n, то есть те частоты, которым соответствуют гармоники с относительно большой ролью в образовании периодического процесса.