1.7.1. Барометрическая формула

Барометрическая формула дает зависимость давления р идеального газа, находящегося в однородном поле тяжести при постоянной температуре Т, от высоты z:

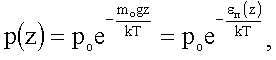(1.20)

где p_o - давление при z = 0, m_o - масса молекулы, k - постоянная Больцмана.

1.7.2. Распределение Больцмана.

Распределение Больцмана позволяет для молекулы, находящейся во внешнем потенциальном поле с энергией ε_n(x, y, z), найти вероятность dw_r того, что эта молекула имеет координаты x, y, z в интервалах dx, dy, dz, соответственно:

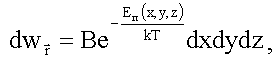(1.21)

здесь В - постоянный множитель, определяемый из условия нормировки:

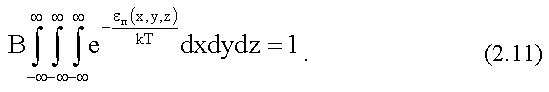. (1.22)

1.7.3. Распределение Максвелла.

Молекулы идеального газа, находящегося в термодинамическом равновесии, вполне определенным образом распределены не только по координатам, но и по проекциям своих скоростей. Как найти такое распределение? Во-первых, следует правильно поставить задачу. Например, постановка задачи в виде: определить количество молекул, имеющих ту или иную заданную скорость, не имеет смысла, потому что это количество математически точно равно нулю! В самом деле, количество молекул, входящих в систему, является хотя и большим, но конечным (равно N). В то же время количество различных значений скорости бесконечно. Поэтому число молекул, приходящихся на долю каждого значения скорости, равно нулю (N/∞ → 0).

Правильная постановка задачи: сколько молекул, или какая часть молекул n = ΔN/N будет иметь скорость V, лежащую в интервале скоростей V + ΔV? Именно так и формулируются статистические задачи. Например, какая часть людей в стране (области, районе) имеют возраст в интервале от 20 до 21 года. Или, например, чтобы прогнозировать, сколько школьных форм определенного размера следует пошить, чтобы обеспечить всех школьников данной местности, следует определить, сколько школьников имеют рост от 149 до 151 см.

Статистическую задачу, какая часть молекул n = ΔN/N будет иметь скорость V, лежащую в интервале скоростей V + ΔV, поставил и решил для идеального газа Д.К. Максвелл.

Максвеллом было получено следующее соотношение:

(1.23)

здесь - вероятность обнаружения молекулы в бесконечно малом прямоугольном параллелепипеде в пространстве скоростей, изображенном на рис. 1.3.

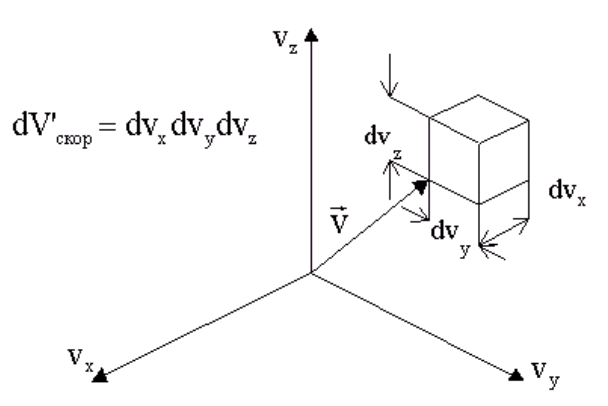
Рис. 1.3

Другими словами, это вероятность того, что молекула имеет проекцию скорости на ось х в интервале от v_х до v_х + dv_х и в подобных же интервалах для значений v_y и v_z.

Из (1.23) видно, что вероятность не зависит от направления вектора , а зависит только от его модуля. Поэтому в формуле (1.23) в качестве элементарного объема в пространстве скоростей вместо прямоугольного параллелепипеда можно взять бесконечно тонкий сферический слой (см. рис. 1.4), радиус которого v, а толщина dv. В этом элементарном объеме все модули скоростей с отклонением, не превышающем dv, равны v. Перейдем, таким образом, от dv_х, dv_y ,dv_z к 4πv²dv, где 4πv² - площадь сферы в пространстве скоростей, изображенной на рис. 1.4.

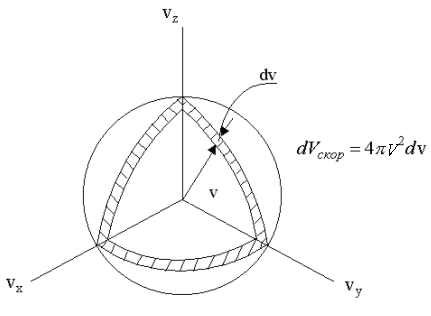
Рис. 1.4.

После чего формула (1.23) принимает вид:

(1.24)

Формулу (1.24) обычно записывают в виде:

(1.25)

где 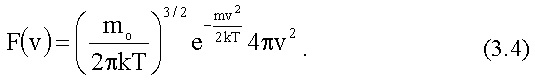(1.26)

Полученную Д.К. Максвеллом функцию F(v) принято называть функцией распределения вероятностей или функцией распределения Максвелла.

Из (1.25) следует, что:

поэтому F(v) называют еще и плотностью вероятности.

График функции распределения Максвелла приведен на рис. 1.5.

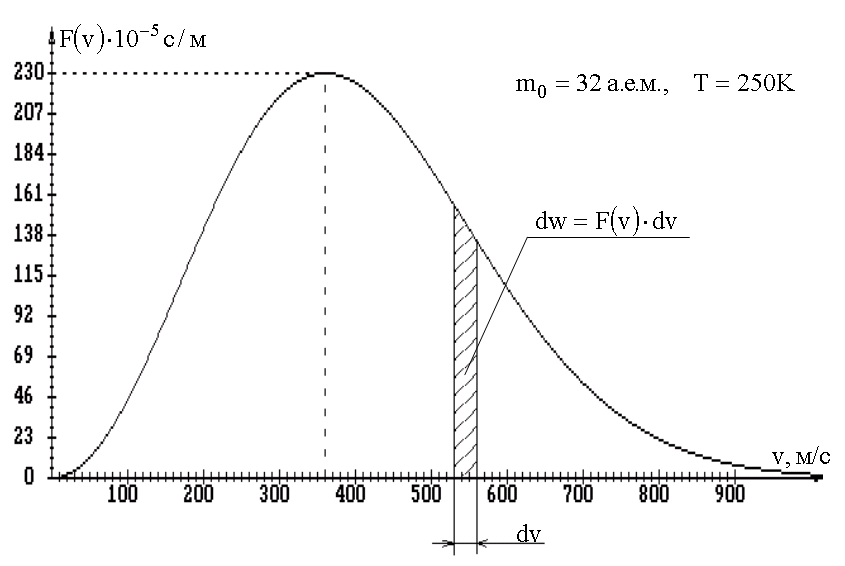
Рис. 1.5.

Свойства распределения Максвелла.

1). При v = 0 множитель v² функции F(v) обращает ее в ноль. Это означает, что нет молекул, которые не двигались бы.

2). При v > 0 функция F(v) растет за счет множителя v². Кривая имеет максимум. Это означает, что существует определенная скорость движения молекул, такая, что вблизи нее на данный интервал dV приходится наибольшая часть молекул. Эта скорость называется наиболее вероятной V_вер.:

(1.27)

Из распределения Максвелла вытекает, что средняя квадратичная скорость выражается

(1.28)

Если учесть, что pV = RT, R = kN_A, μ = m₀N_A, а ρ = μ/V_μ, то из (12) получим другую формулу для средней квадратичной скорости – через макроскопические величины – давление p и плотность ρ:

(1.29)

Средняя кинетическая энергия поступательного движения одной молекулы:

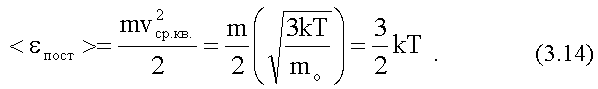(1.30)

что было получено ранее. Таким образом, средняя кинетическая энергия поступательного движения молекул определяется средней квадратичной скоростью.

Средняя арифметическая скорость движения молекул, исходя из распределения Максвелла:

(1.31)

3.) При v → ∞ кривая быстро стремится к нулю за счет экспоненциального множителя. То есть кривая не симметрична: спад кривой в одну сторону больше, чем в другую.

Как видно из формулы (1.26) и рис. 1.5 вероятность dw_v равна площади заштрихованной полоски. Ясно, что вероятность того, что молекула имеет любую скорость, равна сумме площадей всех тонких полосок и, таким образом, площади, ограниченной графиком F(v) и осью скоростей. А площадь этой фигуры не что иное, как интеграл, который, согласно условию нормировки (1.19) и соотношению(1.26), равен единице:

(1.32)

Распределение Максвелла сильно зависит от температуры (рис. 1.6): при увеличении температуры максимум функции F(v) смещается вправо и становится ниже .

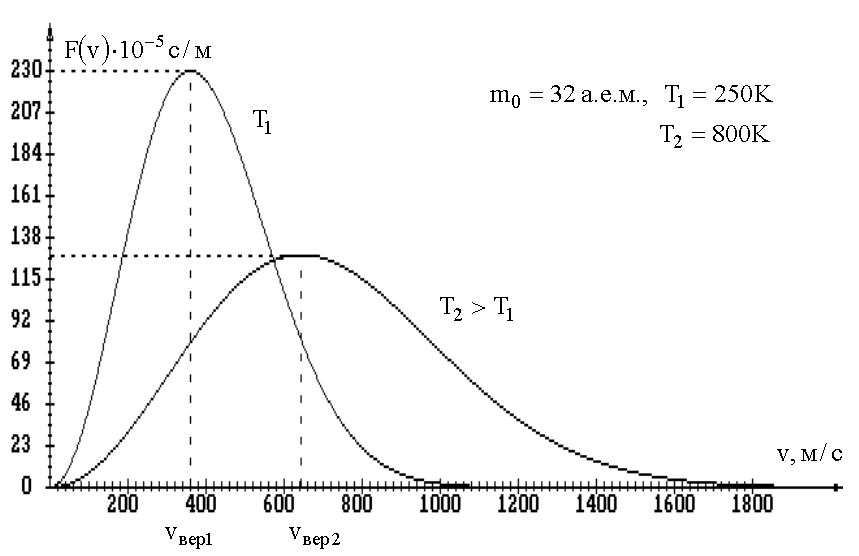
Рис. 1.6.